computability logic on:
[Wikipedia]
[Google]
[Amazon]
Computability logic (CoL) is a research program and mathematical framework for redeveloping
Prepublication
/ref>
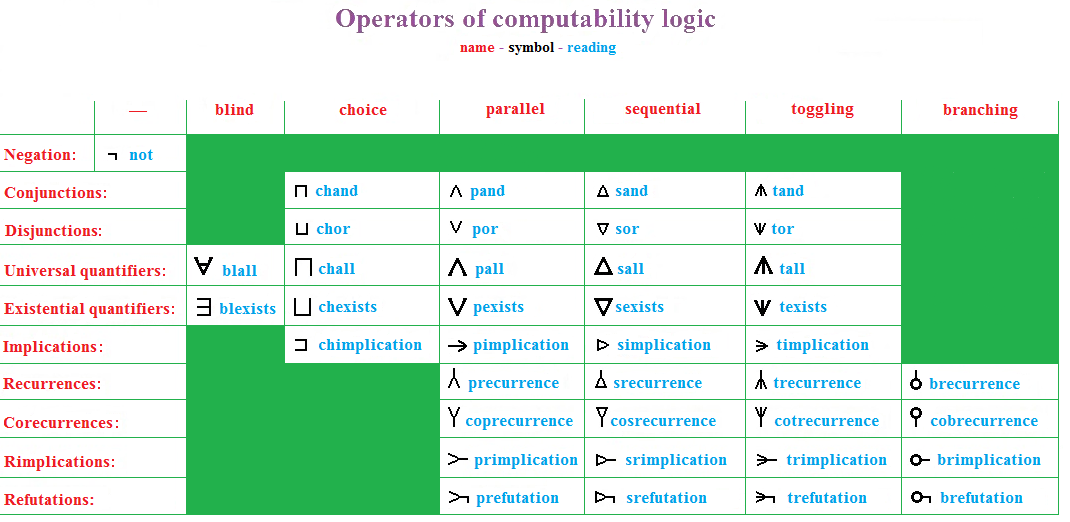 The full language of CoL extends the language of classical
The full language of CoL extends the language of classical
Computability Logic Homepage
Comprehensive survey of the subject.
Giorgi Japaridze
On abstract resource semantics and computabilty logic
Video lecture by N. Vereshchagin.
A Survey of Computability Logic
(PDF) Downloadable equivalent of the above homepage. {{Logic Computability theory Logic in computer science Non-classical logic
logic
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure o ...
as a systematic formal theory of computability, as opposed to classical logic
Classical logic (or standard logic) or Frege–Russell logic is the intensively studied and most widely used class of deductive logic. Classical logic has had much influence on analytic philosophy.
Characteristics
Each logical system in this c ...
, which is a formal theory of truth
Truth or verity is the Property (philosophy), property of being in accord with fact or reality.Merriam-Webster's Online Dictionarytruth, 2005 In everyday language, it is typically ascribed to things that aim to represent reality or otherwise cor ...
. It was introduced and so named by Giorgi Japaridze in 2003.
In classical logic, formula
In science, a formula is a concise way of expressing information symbolically, as in a mathematical formula or a ''chemical formula''. The informal use of the term ''formula'' in science refers to the general construct of a relationship betwe ...
s represent true/false statements. In CoL, formulas represent computational problem
In theoretical computer science, a computational problem is one that asks for a solution in terms of an algorithm. For example, the problem of factoring
:"Given a positive integer ''n'', find a nontrivial prime factor of ''n''."
is a computati ...
s. In classical logic, the validity of an argument depends only on its form, not on its meaning. In CoL, validity means being always computable. More generally, classical logic tells us when the truth of a given statement always follows from the truth of a given set of other statements. Similarly, CoL tells us when the computability of a given problem ''A'' always follows from the computability of other given problems ''B1,...,Bn''. Moreover, it provides a uniform way to actually construct a solution (algorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algo ...
) for such an ''A'' from any known solutions of ''B1,...,Bn''.
CoL formulates computational problems in their most general—interactive
Across the many fields concerned with interactivity, including information science, computer science, human-computer interaction, communication, and industrial design, there is little agreement over the meaning of the term "interactivity", but mo ...
—sense. CoL defines a ''computational problem'' as a game played by a machine against its environment. Such a problem is ''computable'' if there is a machine that wins the game against every possible behavior of the environment. Such a game-playing machine generalizes the Church–Turing thesis
In Computability theory (computation), computability theory, the Church–Turing thesis (also known as computability thesis, the Turing–Church thesis, the Church–Turing conjecture, Church's thesis, Church's conjecture, and Turing's thesis) ...
to the interactive level. The classical concept of truth turns out to be a special, zero-interactivity-degree case of computability. This makes classical logic a special fragment of CoL. Thus CoL is a conservative extension of classical logic. Computability logic is more expressive, constructive and computationally meaningful than classical logic. Besides classical logic, independence-friendly (IF) logic and certain proper extensions of linear logic and intuitionistic logic
Intuitionistic logic, sometimes more generally called constructive logic, refers to systems of symbolic logic that differ from the systems used for classical logic by more closely mirroring the notion of constructive proof. In particular, systems ...
also turn out to be natural fragments of CoL. Hence meaningful concepts of "intuitionistic truth", "linear-logic truth" and "IF-logic truth" can be derived from the semantics of CoL.
CoL systematically answers the fundamental question of what can be computed and how; thus CoL has many applications, such as constructive applied theories, knowledge base
In computer science, a knowledge base (KB) is a set of sentences, each sentence given in a knowledge representation language, with interfaces to tell new sentences and to ask questions about what is known, where either of these interfaces migh ...
systems, systems for planning and action. Out of these, only applications in constructive applied theories have been extensively explored so far: a series of CoL-based number theories, termed "clarithmetics", have been constructed as computationally and complexity-theoretically meaningful alternatives to the classical-logic-based first-order Peano arithmetic and its variations such as systems of bounded arithmetic.
Traditional proof systems such as natural deduction and sequent calculus
In mathematical logic, sequent calculus is a style of formal logical argumentation in which every line of a proof is a conditional tautology (called a sequent by Gerhard Gentzen) instead of an unconditional tautology. Each conditional tautolog ...
are insufficient for axiomatizing nontrivial fragments of CoL. This has necessitated developing alternative, more general and flexible methods of proof, such as cirquent calculus.G. Japaridze, ''The taming of recurrences in computability logic through cirquent calculus, Part I''. Archive for Mathematical Logic 52 (2013), pp. 173–212.Prepublication
/ref>
Language
 The full language of CoL extends the language of classical
The full language of CoL extends the language of classical first-order logic
First-order logic, also called predicate logic, predicate calculus, or quantificational logic, is a collection of formal systems used in mathematics, philosophy, linguistics, and computer science. First-order logic uses quantified variables over ...
. Its logical vocabulary has several sorts of conjunctions, disjunction
In logic, disjunction (also known as logical disjunction, logical or, logical addition, or inclusive disjunction) is a logical connective typically notated as \lor and read aloud as "or". For instance, the English language sentence "it is ...
s, quantifiers, implications, negation
In logic, negation, also called the logical not or logical complement, is an operation (mathematics), operation that takes a Proposition (mathematics), proposition P to another proposition "not P", written \neg P, \mathord P, P^\prime or \over ...
s and so called recurrence operators. This collection includes all connectives and quantifiers of classical logic. The language also has two sorts of nonlogical atoms: ''elementary'' and ''general''. Elementary atoms, which are nothing but the atoms of classical logic, represent ''elementary problems'', i.e., games with no moves that are automatically won by the machine when true and lost when false. General atoms, on the other hand, can be interpreted as any games, elementary or non-elementary. Both semantically and syntactically, classical logic is nothing but the fragment of CoL obtained by forbidding general atoms in its language, and forbidding all operators other than ¬, ∧, ∨, →, ∀, ∃.
Japaridze has repeatedly pointed out that the language of CoL is open-ended, and may undergo further extensions. Due to the expressiveness of this language, advances in CoL, such as constructing axiomatizations or building CoL-based applied theories, have usually been limited to one or another proper fragment of the language.
Semantics
The games underlying the semantics of CoL are called ''static games''. Such games have no turn order; a player can always move while the other players are "thinking". However, static games never punishes a player for "thinking" too long (delaying its own moves), so such games never become contests of speed. All elementary games are automatically static, and so are the games allowed to be interpretations of general atoms. There are two players in static games: the ''machine'' and the ''environment''. The machine can only follow algorithmic strategies, while there are no restrictions on the behavior of the environment. Each run (play) is won by one of these players and lost by the other. The logical operators of CoL are understood as operations on games. Here we informally survey some of those operations. For simplicity we assume that the domain of discourse is always the set of all natural numbers: . The operation ¬ of ''negation'' ("not") switches the roles of the two players, turning moves and wins by the machine into those by the environment, and vice versa. For instance, if ''Chess'' is the game of chess (but with ties ruled out) from the white player's perspective, then ¬''Chess'' is the same game from the black player's perspective. The ''parallel conjunction'' ∧ ("pand") and ''parallel disjunction'' ∨ ("por") combine games in a parallel fashion. A run of ''A''∧''B'' or ''A''∨''B'' is a simultaneous play in the two conjuncts. The machine wins ''A''∧''B'' if it wins both of them. The machine wins ''A''∨''B'' if it wins at least one of them. For example, ''Chess''∨¬''Chess'' is a game on two boards, one played white and one black, and where the task of the machine is to win on at least one board. Such a game can be easily won regardless who the adversary is, by copying his moves from one board to the other. The ''parallel implication'' operator → ("pimplication") is defined by ''A''→''B'' = ¬''A''∨''B''. The intuitive meaning of this operation is ''reducing'' ''B'' to ''A'', i.e., solving ''A'' as long as the adversary solves ''B''. The ''parallel quantifiers'' ∧ ("pall") and ∨ ("pexists") can be defined by ∧''xA''(''x'') = ''A''(0)∧''A''(1)∧''A''(2)∧... and ∨''xA''(''x'') = ''A''(0)∨''A''(1)∨''A''(2)∨.... These are thus simultaneous plays of ''A''(0),''A''(1),''A''(2),..., each on a separate board. The machine wins ∧''xA''(''x'') if it wins all of these games, and ∨''xA''(''x'') if it wins some. The ''blind quantifiers'' ∀ ("blall") and ∃ ("blexists"), on the other hand, generate single-board games. A run of ∀''xA''(''x'') or ∃''xA''(''x'') is a single run of ''A''. The machine wins ∀''xA''(''x'') (respectively ∃''xA''(''x'')) if such a run is a won run of ''A''(''x'') for all (respectively at least one) possible values of ''x'', and wins ∃''xA''(''x'') if this is true for at least one. All of the operators characterized so far behave exactly like their classical counterparts when they are applied to elementary (moveless) games, and validate the same principles. This is why CoL uses the same symbols for those operators as classical logic does. When such operators are applied to non-elementary games, however, their behavior is no longer classical. So, for instance, if ''p'' is an elementary atom and ''P'' a general atom, ''p''→''p''∧''p'' is valid while ''P''→''P''∧''P'' is not. The principle of the excluded middle ''P''∨¬''P'', however, remains valid. The same principle is invalid with all three other sorts (choice, sequential and toggling) of disjunction. The ''choice disjunction'' ⊔ ("chor") of games ''A'' and ''B'', written ''A''⊔''B'', is a game where, in order to win, the machine has to choose one of the two disjuncts and then win in the chosen component. The ''sequential disjunction'' ("sor") ''A''ᐁ''B'' starts as ''A''; it also ends as ''A'' unless the machine makes a "switch" move, in which case ''A'' is abandoned and the game restarts and continues as ''B''. In the ''toggling disjunction'' ("tor") ''A''⩛''B'', the machine may switch between ''A'' and ''B'' any finite number of times. Each disjunction operator has its dual conjunction, obtained by interchanging the roles of the two players. The corresponding quantifiers can further be defined as infinite conjunctions or disjunctions in the same way as in the case of the parallel quantifiers. Each sort of disjunction also induces a corresponding implication operation the same way as this was the case with the parallel implication →. For instance, the ''choice implication'' ("chimplication") ''A''⊐''B'' is defined as ¬''A''⊔''B''. The ''parallel recurrence'' ("precurrence") of ''A'' can be defined as the infinite parallel conjunction ''A''∧A∧A∧... The sequential ("srecurrence") and toggling ("trecurrence") sorts of recurrences can be defined similarly. The ''corecurrence'' operators can be defined as infinite disjunctions. ''Branching recurrence'' ("brecurrence") ⫰, which is the strongest sort of recurrence, does not have a corresponding conjunction. ⫰''A'' is a game that starts and proceeds as ''A''. At any time, however, the environment is allowed to make a "replicative" move, which creates two copies of the then-current position of ''A'', thus splitting the play into two parallel threads with a common past but possibly different future developments. In the same fashion, the environment can further replicate any of positions of any thread, thus creating more and more threads of ''A''. Those threads are played in parallel, and the machine needs to win ''A'' in all threads to be the winner in ⫰''A''. ''Branching corecurrence'' ("cobrecurrence") ⫯ is defined symmetrically by interchanging "machine" and "environment". Each sort of recurrence further induces a corresponding weak version of implication and weak version of negation. The former is said to be a ''rimplication'', and the latter a ''refutation''. The ''branching rimplication'' ("brimplication") ''A''⟜''B'' is nothing but ⫰''A''→''B'', and the ''branching refutation'' ("brefutation") of ''A'' is ''A''⟜⊥, where ⊥ is the always-lost elementary game. Similarly for all other sorts of rimplication and refutation.As a problem specification tool
The language of CoL offers a systematic way to specify an infinite variety of computational problems, with or without names established in the literature. Below are some examples. Let ''f'' be a unary function. The problem of computing ''f'' will be written as ⊓x⊔y(''y''=''f''(''x'')). According to the semantics of CoL, this is a game where the first move ("input") is by the environment, which should choose a value ''m'' for ''x''. Intuitively, this amounts to asking the machine to tell the value of ''f''(''m''). The game continues as ⊔y(''y''=''f''(''m'')). Now the machine is expected to make a move ("output"), which should be choosing a value ''n'' for ''y''. This amounts to saying that ''n'' is the value of ''f''(m). The game is now brought down to the elementary ''n''=''f''(''m''), which is won by the machine if and only if ''n'' is indeed the value of ''f''(''m''). Let ''p'' be a unary predicate. Then ⊓''x''(''p''(''x'')⊔¬''p''(''x'')) expresses the problem of deciding ''p'', ⊓''x''(''p''(''x'')&ᐁ¬''p''(''x'')) expresses the problem of semideciding ''p'', and ⊓''x''(''p''(''x'')⩛¬''p''(''x'')) the problem of recursively approximating ''p''. Let ''p'' and ''q'' be two unary predicates. Then ⊓''x''(''p''(''x'')⊔¬''p''(''x''))⟜⊓''x''(''q''(''x'')⊔¬''q''(''x'')) expresses the problem of Turing-reducing ''q'' to ''p'' (in the sense that ''q'' is Turing reducible to ''p'' if and only if the interactive problem ⊓''x''(''p''(''x'')⊔¬''p''(''x''))⟜⊓''x''(''q''(''x'')⊔¬''q''(''x'')) is computable). ⊓''x''(''p''(''x'')⊔¬''p''(''x''))→⊓''x''(''q''(''x'')⊔¬''q''(''x'')) does the same but for the stronger version of Turing reduction where theoracle
An oracle is a person or thing considered to provide insight, wise counsel or prophetic predictions, most notably including precognition of the future, inspired by deities. If done through occultic means, it is a form of divination.
Descript ...
for ''p'' can be queried only once. ⊓x⊔''y''(''q''(''x'')↔''p''(''y'')) does the same for the problem of many-one reducing ''q'' to ''p''. With more complex expressions one can capture all kinds of nameless yet potentially meaningful relations and operations on computational problems, such as, for instance, "Turing-reducing the problem of semideciding ''r'' to the problem of many-one reducing ''q'' to ''p''". Imposing time or space restrictions on the work of the machine, one further gets complexity-theoretic counterparts of such relations and operations.
As a problem solving tool
The known deductive systems for various fragments of CoL share the property that a solution (algorithm) can be automatically extracted from a proof of a problem in the system. This property is further inherited by all applied theories based on those systems. So, in order to find a solution for a given problem, it is sufficient to express it in the language of CoL and then find a proof of that expression. Another way to look at this phenomenon is to think of a formula ''G'' of CoL as program specification (goal). Then a proof of ''G'' is – more precisely, translates into – a program meeting that specification. There is no need to verify that the specification is met, because the proof itself is, in fact, such a verification. Examples of CoL-based applied theories are the so-called ''clarithmetics''. These are number theories based on CoL in the same sense as first-order Peano arithmetic PA is based on classical logic. Such a system is usually a conservative extension of PA. It typically includes all Peano axioms, and adds to them one or two extra-Peano axioms such as ⊓''x''⊔''y''(''y''=''x) expressing the computability of the successor function. Typically it also has one or two non-logical rules of inference, such as constructive versions of induction or comprehension. Through routine variations in such rules one can obtainsound
In physics, sound is a vibration that propagates as an acoustic wave through a transmission medium such as a gas, liquid or solid.
In human physiology and psychology, sound is the ''reception'' of such waves and their ''perception'' by the br ...
and complete systems characterizing one or another interactive computational complexity class ''C''. This is in the sense that a problem belongs to ''C'' if and only if it has a proof in the theory. So, such a theory can be used for finding not merely algorithmic solutions, but also efficient ones on demand, such as solutions that run in polynomial time or logarithmic space. It should be pointed out that all clarithmetical theories share the same logical postulates, and only their non-logical postulates vary depending on the target complexity class. Their notable distinguishing feature from other approaches with similar aspirations (such as bounded arithmetic) is that they extend rather than weaken PA, preserving the full deductive power and convenience of the latter.
See also
* Game semantics * Interactive computation *Logic
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure o ...
* Logics for computability
References
External links
Computability Logic Homepage
Comprehensive survey of the subject.
Giorgi Japaridze
On abstract resource semantics and computabilty logic
Video lecture by N. Vereshchagin.
A Survey of Computability Logic
(PDF) Downloadable equivalent of the above homepage. {{Logic Computability theory Logic in computer science Non-classical logic