chemical potential on:
[Wikipedia]
[Google]
[Amazon]
In
Thermal Physics
' by Kittel and Kroemer, second edition, page 124. If two locations have different total chemical potentials for a species, some of it may be due to potentials associated with "external" force fields ( electric potential energy,
Hadrons and Quark-Gluon Plasma
by Jean Letessier, Johann Rafelski, p. 91.
In the case of electrons, the behaviour depends on temperature and context. At low temperatures, with no positrons present, electrons cannot be created or destroyed. Therefore, there is an electron chemical potential that might vary in space, causing diffusion. At very high temperatures, however, electrons and positrons can spontaneously appear out of the vacuum (
 Generally the chemical potential is given as a sum of an ideal contribution and an excess contribution:
:
In an ideal solution, the chemical potential of species ''i'' (μ''i'') is dependent on temperature and pressure.
μ''i''0(''T'', ''P'') is defined as the chemical potential of pure species ''i''. Given this definition, the chemical potential of species ''i'' in an ideal solution is
:
where ''R'' is the gas constant, and is the mole fraction of species ''i'' contained in the solution. The chemical potential becomes negative infinity when , but this does not lead to nonphysical results because means that species ''i'' is not present in the system.
This equation assumes that only depends on the mole fraction () contained in the solution. This neglects intermolecular interaction between species ''i'' with itself and other species 'i''–(''j''≠''i'') This can be corrected for by factoring in the coefficient of activity of species ''i'', defined as γ''i''. This correction yields
:
The plots above give a very rough picture of the ideal and non-ideal situation.
Generally the chemical potential is given as a sum of an ideal contribution and an excess contribution:
:
In an ideal solution, the chemical potential of species ''i'' (μ''i'') is dependent on temperature and pressure.
μ''i''0(''T'', ''P'') is defined as the chemical potential of pure species ''i''. Given this definition, the chemical potential of species ''i'' in an ideal solution is
:
where ''R'' is the gas constant, and is the mole fraction of species ''i'' contained in the solution. The chemical potential becomes negative infinity when , but this does not lead to nonphysical results because means that species ''i'' is not present in the system.
This equation assumes that only depends on the mole fraction () contained in the solution. This neglects intermolecular interaction between species ''i'' with itself and other species 'i''–(''j''≠''i'') This can be corrected for by factoring in the coefficient of activity of species ''i'', defined as γ''i''. This correction yields
:
The plots above give a very rough picture of the ideal and non-ideal situation.
thermodynamics
Thermodynamics is a branch of physics that deals with heat, work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior of these quantities is governed by the four laws of the ...
, the chemical potential of a species
In biology, a species is the basic unit of classification and a taxonomic rank of an organism, as well as a unit of biodiversity. A species is often defined as the largest group of organisms in which any two individuals of the appropriate s ...
is the energy
In physics, energy (from Ancient Greek: ἐνέργεια, ''enérgeia'', “activity”) is the quantitative property that is transferred to a body or to a physical system, recognizable in the performance of work and in the form of heat a ...
that can be absorbed or released due to a change of the particle number of the given species, e.g. in a chemical reaction or phase transition
In chemistry, thermodynamics, and other related fields, a phase transition (or phase change) is the physical process of transition between one state of a medium and another. Commonly the term is used to refer to changes among the basic states of ...
. The chemical potential of a species in a mixture is defined as the rate of change of free energy of a thermodynamic system
A thermodynamic system is a body of matter and/or radiation, confined in space by walls, with defined permeabilities, which separate it from its surroundings. The surroundings may include other thermodynamic systems, or physical systems that are ...
with respect to the change in the number of atoms or molecules of the species that are added to the system. Thus, it is the partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant (as opposed to the total derivative, in which all variables are allowed to vary). Part ...
of the free energy with respect to the amount of the species, all other species' concentrations in the mixture remaining constant. When both temperature and pressure are held constant, and the number of particles is expressed in moles, the chemical potential is the partial molar Gibbs free energy
In thermodynamics, the Gibbs free energy (or Gibbs energy; symbol G) is a thermodynamic potential that can be used to calculate the maximum amount of work that may be performed by a thermodynamically closed system at constant temperature and ...
. At chemical equilibrium
In a chemical reaction, chemical equilibrium is the state in which both the Reagent, reactants and Product (chemistry), products are present in concentrations which have no further tendency to change with time, so that there is no observable chan ...
or in phase equilibrium
In thermodynamics, the phase rule is a general principle governing "pVT" systems, whose thermodynamic states are completely described by the variables pressure (), volume () and temperature (), in thermodynamic equilibrium. If is the number of ...
, the total sum of the product of chemical potentials and stoichiometric coefficient
A chemical equation is the symbolic representation of a chemical reaction in the form of symbols and chemical formulas. The reactant entities are given on the left-hand side and the product entities on the right-hand side with a plus sign between ...
s is zero, as the free energy is at a minimum. In a system in diffusion equilibrium, the chemical potential of any chemical species is uniformly the same everywhere throughout the system.Atkins (7th ed.), Section 6.4, p. 141.
In semiconductor
A semiconductor is a material which has an electrical resistivity and conductivity, electrical conductivity value falling between that of a electrical conductor, conductor, such as copper, and an insulator (electricity), insulator, such as glas ...
physics, the chemical potential of a system of electrons at zero absolute temperature is known as the Fermi energy
The Fermi energy is a concept in quantum mechanics usually referring to the energy difference between the highest and lowest occupied single-particle states in a quantum system of non-interacting fermions at absolute zero temperature.
In a Fermi ga ...
.
Overview
Particles tend to move from higher chemical potential to lower chemical potential because this reduces the free energy. In this way, chemical potential is a generalization of "potentials" in physics such asgravitational potential
In classical mechanics, the gravitational potential at a location is equal to the work (energy transferred) per unit mass that would be needed to move an object to that location from a fixed reference location. It is analogous to the electric ...
. When a ball rolls down a hill, it is moving from a higher gravitational potential (higher internal energy thus higher potential for work) to a lower gravitational potential (lower internal energy). In the same way, as molecules move, react, dissolve, melt, etc., they will always tend naturally to go from a higher chemical potential to a lower one, changing the particle number, which is the conjugate variable
Conjugate variables are pairs of variables mathematically defined in such a way that they become Fourier transform duals, or more generally are related through Pontryagin duality. The duality relations lead naturally to an uncertainty relation— ...
to chemical potential.
A simple example is a system of dilute molecules diffusing
Molecular diffusion, often simply called diffusion, is the thermal motion of all (liquid or gas) particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size (mass) of ...
in a homogeneous environment. In this system, the molecules tend to move from areas with high concentration
In chemistry, concentration is the abundance of a constituent divided by the total volume of a mixture. Several types of mathematical description can be distinguished: '' mass concentration'', ''molar concentration'', ''number concentration'', an ...
to low concentration, until eventually, the concentration is the same everywhere. The microscopic explanation for this is based on kinetic theory
Kinetic (Ancient Greek: κίνησις “kinesis”, movement or to move) may refer to:
* Kinetic theory, describing a gas as particles in random motion
* Kinetic energy, the energy of an object that it possesses due to its motion
Art and ente ...
and the random motion of molecules. However, it is simpler to describe the process in terms of chemical potentials: For a given temperature, a molecule has a higher chemical potential in a higher-concentration area and a lower chemical potential in a low concentration area. Movement of molecules from higher chemical potential to lower chemical potential is accompanied by a release of free energy. Therefore, it is a spontaneous process In thermodynamics, a spontaneous process is a process which occurs without any external input to the system. A more technical definition is the time-evolution of a system in which it releases free energy and it moves to a lower, more thermodynamic ...
.
Another example, not based on concentration but on phase, is an ice cube on a plate above 0 °C. An H2O molecule that is in the solid phase (ice) has a higher chemical potential than a water molecule that is in the liquid phase (water) above 0 °C. When some of the ice melts, H2O molecules convert from solid to the warmer liquid where their chemical potential is lower, so the ice cube shrinks. At the temperature of the melting point
The melting point (or, rarely, liquefaction point) of a substance is the temperature at which it changes state from solid to liquid. At the melting point the solid and liquid phase exist in equilibrium. The melting point of a substance depends ...
, 0 °C, the chemical potentials in water and ice are the same; the ice cube neither grows nor shrinks, and the system is in equilibrium.
A third example is illustrated by the chemical reaction
A chemical reaction is a process that leads to the IUPAC nomenclature for organic transformations, chemical transformation of one set of chemical substances to another. Classically, chemical reactions encompass changes that only involve the pos ...
of dissociation
Dissociation, in the wide sense of the word, is an act of disuniting or separating a complex object into parts. Dissociation may also refer to:
* Dissociation (chemistry), general process in which molecules or ionic compounds (complexes, or salts ...
of a weak acid
Acid strength is the tendency of an acid, symbolised by the chemical formula HA, to dissociate into a proton, H+, and an anion, A-. The dissociation of a strong acid in solution is effectively complete, except in its most concentrated solutions ...
HA (such as acetic acid
Acetic acid , systematically named ethanoic acid , is an acidic, colourless liquid and organic compound with the chemical formula (also written as , , or ). Vinegar is at least 4% acetic acid by volume, making acetic acid the main component ...
, A = CH3COO−):
:HA H+ + A−
Vinegar
Vinegar is an aqueous solution of acetic acid and trace compounds that may include flavorings. Vinegar typically contains 5–8% acetic acid by volume. Usually, the acetic acid is produced by a double fermentation, converting simple sugars to eth ...
contains acetic acid. When acid molecules dissociate, the concentration of the undissociated acid molecules (HA) decreases and the concentrations of the product ions (H+ and A−) increase. Thus the chemical potential of HA decreases and the sum of the chemical potentials of H+ and A− increases. When the sums of chemical potential of reactants and products are equal the system is at equilibrium and there is no tendency for the reaction to proceed in either the forward or backward direction. This explains why vinegar is acidic, because acetic acid dissociates to some extent, releasing hydrogen ion
A hydrogen ion is created when a hydrogen atom loses or gains an electron. A positively charged hydrogen ion (or proton) can readily combine with other particles and therefore is only seen isolated when it is in a gaseous state or a nearly particle ...
s into the solution.
Chemical potentials are important in many aspects of multi-phase equilibrium chemistry
Equilibrium chemistry is concerned with systems in chemical equilibrium. The unifying principle is that the free energy of a system at equilibrium is the minimum possible, so that the slope of the free energy with respect to the reaction coordin ...
, including melting
Melting, or fusion, is a physical process that results in the phase transition of a substance from a solid to a liquid. This occurs when the internal energy of the solid increases, typically by the application of heat or pressure, which inc ...
, boiling, evaporation
Evaporation is a type of vaporization that occurs on the surface of a liquid as it changes into the gas phase. High concentration of the evaporating substance in the surrounding gas significantly slows down evaporation, such as when humidi ...
, solubility
In chemistry, solubility is the ability of a substance, the solute, to form a solution with another substance, the solvent. Insolubility is the opposite property, the inability of the solute to form such a solution.
The extent of the solubil ...
, osmosis
Osmosis (, ) is the spontaneous net movement or diffusion of solvent molecules through a selectively-permeable membrane from a region of high water potential (region of lower solute concentration) to a region of low water potential (region of ...
, partition coefficient
In the physical sciences, a partition coefficient (''P'') or distribution coefficient (''D'') is the ratio of concentrations of a compound in a mixture of two immiscible solvents at equilibrium. This ratio is therefore a comparison of the solub ...
, liquid-liquid extraction and chromatography
In chemical analysis, chromatography is a laboratory technique for the separation of a mixture into its components. The mixture is dissolved in a fluid solvent (gas or liquid) called the ''mobile phase'', which carries it through a system ( ...
. In each case the chemical potential of a given species at equilibrium is the same in all phases of the system.
In electrochemistry
Electrochemistry is the branch of physical chemistry concerned with the relationship between electrical potential difference, as a measurable and quantitative phenomenon, and identifiable chemical change, with the potential difference as an outco ...
, ion
An ion () is an atom or molecule with a net electrical charge.
The charge of an electron is considered to be negative by convention and this charge is equal and opposite to the charge of a proton, which is considered to be positive by conve ...
s do ''not'' always tend to go from higher to lower chemical potential, but they ''do'' always go from higher to lower ''electrochemical potential
In electrochemistry, the electrochemical potential (ECP), ', is a thermodynamic measure of chemical potential that does not omit the energy contribution of electrostatics. Electrochemical potential is expressed in the unit of J/ mol.
Introductio ...
''. The electrochemical potential completely characterizes all of the influences on an ion's motion, while the chemical potential includes everything ''except'' the electric force
Coulomb's inverse-square law, or simply Coulomb's law, is an experimental law of physics that quantifies the amount of force between two stationary, electrically charged particles. The electric force between charged bodies at rest is convention ...
. (See below for more on this terminology.)
Thermodynamic definition
The chemical potential ''μ''''i'' of species ''i'' (atomic, molecular or nuclear) is defined, as allintensive
In grammar, an intensive word form is one which denotes stronger, more forceful, or more concentrated action relative to the root on which the intensive is built. Intensives are usually lexical formations, but there may be a regular process for for ...
quantities are, by the phenomenological fundamental equation of thermodynamics. This holds for both reversible and irreversible infinitesimal processes:
:
where d''U'' is the infinitesimal change of internal energy
The internal energy of a thermodynamic system is the total energy contained within it. It is the energy necessary to create or prepare the system in its given internal state, and includes the contributions of potential energy and internal kinet ...
''U'', d''S'' the infinitesimal change of entropy
Entropy is a scientific concept, as well as a measurable physical property, that is most commonly associated with a state of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynam ...
''S'', d''V'' is the infinitesimal change of volume
Volume is a measure of occupied three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch). Th ...
''V'' for a thermodynamic system
A thermodynamic system is a body of matter and/or radiation, confined in space by walls, with defined permeabilities, which separate it from its surroundings. The surroundings may include other thermodynamic systems, or physical systems that are ...
in thermal equilibrium, and d''N''''i'' is the infinitesimal change of particle number ''N''''i'' of species ''i'' as particles are added or subtracted. ''T'' is absolute temperature
Thermodynamic temperature is a quantity defined in thermodynamics as distinct from kinetic theory or statistical mechanics.
Historically, thermodynamic temperature was defined by Kelvin in terms of a macroscopic relation between thermodynamic wor ...
, ''S'' is entropy
Entropy is a scientific concept, as well as a measurable physical property, that is most commonly associated with a state of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynam ...
, ''P'' is pressure, and ''V'' is volume. Other work terms, such as those involving electric, magnetic or gravitational fields may be added.
From the above equation, the chemical potential is given by
:
This is an inconvenient expression for condensed-matter systems, such as chemical solutions, as it is hard to control the volume and entropy to be constant while particles are added. A more convenient expression may be obtained by making a Legendre transformation
In mathematics, the Legendre transformation (or Legendre transform), named after Adrien-Marie Legendre, is an involutive transformation on real-valued convex functions of one real variable. In physical problems, it is used to convert functions ...
to another thermodynamic potential: the Gibbs free energy
In thermodynamics, the Gibbs free energy (or Gibbs energy; symbol G) is a thermodynamic potential that can be used to calculate the maximum amount of work that may be performed by a thermodynamically closed system at constant temperature and ...
. From the differential and using the above expression for , a differential relation for is obtained:
:
As a consequence, another expression for results:
:
and the change in Gibbs free energy of a system that is held at constant temperature and pressure is simply
:
In thermodynamic equilibrium, when the system concerned is at constant temperature and pressure but can exchange particles with its external environment, the Gibbs free energy is at its minimum for the system, that is . It follows that
:
Use of this equality provides the means to establish the equilibrium constant
The equilibrium constant of a chemical reaction is the value of its reaction quotient at chemical equilibrium, a state approached by a dynamic chemical system after sufficient time has elapsed at which its composition has no measurable tendency ...
for a chemical reaction.
By making further Legendre transformations from ''U'' to other thermodynamic potentials like the enthalpy
Enthalpy , a property of a thermodynamic system, is the sum of the system's internal energy and the product of its pressure and volume. It is a state function used in many measurements in chemical, biological, and physical systems at a constant ...
and Helmholtz free energy
In thermodynamics, the Helmholtz free energy (or Helmholtz energy) is a thermodynamic potential that measures the useful work obtainable from a closed thermodynamic system at a constant temperature (isothermal
In thermodynamics, an isotherma ...
, expressions for the chemical potential may be obtained in terms of these:
:
:
These different forms for the chemical potential are all equivalent, meaning that they have the same physical content and may be useful in different physical situations.
Applications
TheGibbs–Duhem equation In thermodynamics, the Gibbs–Duhem equation describes the relationship between changes in chemical potential for components in a thermodynamic system:
:\sum_^I N_i \mathrm\mu_i = - S \mathrmT + V \mathrmp
where N_i is the number of moles of com ...
is useful because it relates individual chemical potentials. For example, in a binary mixture, at constant temperature and pressure, the chemical potentials of the two participants A and B are related by
:
where is the number of moles of A and is the number of moles of B. Every instance of phase or chemical equilibrium is characterized by a constant. For instance, the melting of ice is characterized by a temperature, known as the melting point
The melting point (or, rarely, liquefaction point) of a substance is the temperature at which it changes state from solid to liquid. At the melting point the solid and liquid phase exist in equilibrium. The melting point of a substance depends ...
at which solid and liquid phases are in equilibrium with each other. Chemical potentials can be used to explain the slopes of lines on a phase diagram by using the Clapeyron equation, which in turn can be derived from the Gibbs–Duhem equation. They are used to explain colligative properties
In chemistry, colligative properties are those properties of solutions that depend on the ratio of the number of solute particles to the number of solvent particles in a solution, and not on the nature of the chemical species present. The number ...
such as melting-point depression
:''This article deals with melting/freezing point depression due to very small particle size. For depression due to the mixture of another compound, see freezing-point depression.''
Melting-point depression is the phenomenon of reduction of the m ...
by the application of pressure. Henry's law
In physical chemistry, Henry's law is a gas law that states that the amount of dissolved gas in a liquid is directly proportional to its partial pressure above the liquid. The proportionality factor is called Henry's law constant. It was formulat ...
for the solute can be derived from Raoult's law for the solvent using chemical potentials.McQuarrie, D. A.; Simon, J. D. ''Physical Chemistry – A Molecular Approach'', p. 968, University Science Books, 1997.
History
Chemical potential was first described by the American engineer, chemist and mathematical physicistJosiah Willard Gibbs
Josiah Willard Gibbs (; February 11, 1839 – April 28, 1903) was an American scientist who made significant theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynamics was instrumental in t ...
. He defined it as follows:
Gibbs later noted also that for the purposes of this definition, any chemical element
A chemical element is a species of atoms that have a given number of protons in their nuclei, including the pure substance consisting only of that species. Unlike chemical compounds, chemical elements cannot be broken down into simpler sub ...
or combination of elements in given proportions may be considered a substance, whether capable or not of existing by itself as a homogeneous body. This freedom to choose the boundary of the system allows the chemical potential to be applied to a huge range of systems. The term can be used in thermodynamics
Thermodynamics is a branch of physics that deals with heat, work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior of these quantities is governed by the four laws of the ...
and physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which r ...
for any system undergoing change. Chemical potential is also referred to as partial molar Gibbs energy (see also partial molar property
In thermodynamics, a partial molar property is a quantity which describes the variation of an extensive property of a solution or mixture with changes in the molar composition of the mixture at constant temperature and pressure. It is the part ...
). Chemical potential is measured in units of energy/particle or, equivalently, energy/mole
Mole (or Molé) may refer to:
Animals
* Mole (animal) or "true mole", mammals in the family Talpidae, found in Eurasia and North America
* Golden moles, southern African mammals in the family Chrysochloridae, similar to but unrelated to Talpida ...
.
In his 1873 paper ''A Method of Geometrical Representation of the Thermodynamic Properties of Substances by Means of Surfaces'', Gibbs introduced the preliminary outline of the principles of his new equation able to predict or estimate the tendencies of various natural processes to ensue when bodies or systems are brought into contact. By studying the interactions of homogeneous substances in contact, i.e. bodies, being in composition part solid, part liquid, and part vapor, and by using a three-dimensional volume
Volume is a measure of occupied three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch). Th ...
–entropy
Entropy is a scientific concept, as well as a measurable physical property, that is most commonly associated with a state of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynam ...
–internal energy
The internal energy of a thermodynamic system is the total energy contained within it. It is the energy necessary to create or prepare the system in its given internal state, and includes the contributions of potential energy and internal kinet ...
graph, Gibbs was able to determine three states of equilibrium, i.e. "necessarily stable", "neutral", and "unstable", and whether or not changes will ensue. In 1876, Gibbs built on this framework by introducing the concept of chemical potential so to take into account chemical reactions and states of bodies that are chemically different from each other. In his own words from the aforementioned paper, Gibbs states:
In this description, as used by Gibbs, ''ε'' refers to the internal energy
The internal energy of a thermodynamic system is the total energy contained within it. It is the energy necessary to create or prepare the system in its given internal state, and includes the contributions of potential energy and internal kinet ...
of the body, ''η'' refers to the entropy
Entropy is a scientific concept, as well as a measurable physical property, that is most commonly associated with a state of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynam ...
of the body, and ''ν'' is the volume
Volume is a measure of occupied three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch). Th ...
of the body.
Electrochemical, internal, external, and total chemical potential
The abstract definition of chemical potential given above—total change in free energy per extra mole of substance—is more specifically called total chemical potential.Thermal Physics
' by Kittel and Kroemer, second edition, page 124. If two locations have different total chemical potentials for a species, some of it may be due to potentials associated with "external" force fields ( electric potential energy,
gravitational potential energy
Gravitational energy or gravitational potential energy is the potential energy a massive object has in relation to another massive object due to gravity. It is the potential energy associated with the gravitational field, which is released (conver ...
, etc.), while the rest would be due to "internal" factors (density, temperature, etc.) Therefore, the total chemical potential can be split into internal chemical potential and external chemical potential:
:
where
:
i.e., the external potential is the sum of electric potential, gravitational potential, etc. (where ''q'' and ''m'' are the charge and mass of the species, ''V''ele and ''h'' are the electric potential
The electric potential (also called the ''electric field potential'', potential drop, the electrostatic potential) is defined as the amount of work energy needed to move a unit of electric charge from a reference point to the specific point in ...
Mortimer, R. G. ''Physical Chemistry'', 3rd ed., p. 352, Academic Press, 2008. and height of the container, respectively, and ''g'' is the acceleration due to gravity). The internal chemical potential includes everything else besides the external potentials, such as density, temperature, and enthalpy. This formalism can be understood by assuming that the total energy of a system, , is the sum of two parts: an internal energy, , and an external energy due to the interaction of each particle with an external field, . The definition of chemical potential applied to yields the above expression for .
The phrase "chemical potential" sometimes means "total chemical potential", but that is not universal. In some fields, in particular electrochemistry
Electrochemistry is the branch of physical chemistry concerned with the relationship between electrical potential difference, as a measurable and quantitative phenomenon, and identifiable chemical change, with the potential difference as an outco ...
, semiconductor physics
A semiconductor is a material which has an electrical conductivity value falling between that of a conductor, such as copper, and an insulator, such as glass. Its resistivity falls as its temperature rises; metals behave in the opposite way. ...
, and solid-state physics
Solid-state physics is the study of rigid matter, or solids, through methods such as quantum mechanics, crystallography, electromagnetism, and metallurgy. It is the largest branch of condensed matter physics. Solid-state physics studies how the l ...
, the term "chemical potential" means ''internal'' chemical potential, while the term electrochemical potential
In electrochemistry, the electrochemical potential (ECP), ', is a thermodynamic measure of chemical potential that does not omit the energy contribution of electrostatics. Electrochemical potential is expressed in the unit of J/ mol.
Introductio ...
is used to mean ''total'' chemical potential.
Systems of particles
Electrons in solids
Electrons in solids have a chemical potential, defined the same way as the chemical potential of a chemical species: The change in free energy when electrons are added or removed from the system. In the case of electrons, the chemical potential is usually expressed in energy per particle rather than energy per mole, and the energy per particle is conventionally given in units ofelectronvolt
In physics, an electronvolt (symbol eV, also written electron-volt and electron volt) is the measure of an amount of kinetic energy
In physics, the kinetic energy of an object is the energy that it possesses due to its motion.
It is defi ...
(eV).
Chemical potential plays an especially important role in solid-state physics
Solid-state physics is the study of rigid matter, or solids, through methods such as quantum mechanics, crystallography, electromagnetism, and metallurgy. It is the largest branch of condensed matter physics. Solid-state physics studies how the l ...
and is closely related to the concepts of work function
In solid-state physics, the work function (sometimes spelt workfunction) is the minimum thermodynamic work (i.e., energy) needed to remove an electron from a solid to a point in the vacuum immediately outside the solid surface. Here "immediately" ...
, Fermi energy
The Fermi energy is a concept in quantum mechanics usually referring to the energy difference between the highest and lowest occupied single-particle states in a quantum system of non-interacting fermions at absolute zero temperature.
In a Fermi ga ...
, and Fermi level. For example, n-type silicon has a higher internal chemical potential of electrons than p-type silicon. In a p–n junction diode at equilibrium the chemical potential (''internal'' chemical potential) varies from the p-type to the n-type side, while the total chemical potential
In thermodynamics, the chemical potential of a species is the energy that can be absorbed or released due to a change of the particle number of the given species, e.g. in a chemical reaction or phase transition. The chemical potential of a species ...
(electrochemical potential, or, Fermi level) is constant throughout the diode.
As described above, when describing chemical potential, one has to say "relative to what". In the case of electrons in semiconductors, internal chemical potential is often specified relative to some convenient point in the band structure, e.g., to the bottom of the conduction band. It may also be specified "relative to vacuum", to yield a quantity known as work function
In solid-state physics, the work function (sometimes spelt workfunction) is the minimum thermodynamic work (i.e., energy) needed to remove an electron from a solid to a point in the vacuum immediately outside the solid surface. Here "immediately" ...
, however, work function varies from surface to surface even on a completely homogeneous material. Total chemical potential, on the other hand, is usually specified relative to electrical ground
In electrical engineering, ground or earth is a reference point in an electrical circuit from which voltages are measured, a common return path for electric current, or a direct physical connection to the Earth.
Electrical circuits may be co ...
.
In atomic physics, the chemical potential of the electrons in an atom is sometimes said to be the negative of the atom's electronegativity
Electronegativity, symbolized as , is the tendency for an atom of a given chemical element to attract shared electrons (or electron density) when forming a chemical bond. An atom's electronegativity is affected by both its atomic number and the d ...
. Likewise, the process of chemical potential equalization is sometimes referred to as the process of electronegativity equalization
Electronegativity, symbolized as , is the tendency for an atom of a given chemical element to attract shared electrons (or electron density) when forming a chemical bond. An atom's electronegativity is affected by both its atomic number and the d ...
. This connection comes from the Mulliken electronegativity
Electronegativity, symbolized as , is the tendency for an atom of a given chemical element to attract shared electrons (or electron density) when forming a chemical bond. An atom's electronegativity is affected by both its atomic number and the d ...
scale. By inserting the energetic definitions of the ionization potential
Ionization, or Ionisation is the process by which an atom or a molecule acquires a negative or positive charge by gaining or losing electrons, often in conjunction with other chemical changes. The resulting electrically charged atom or molecule ...
and electron affinity
The electron affinity (''E''ea) of an atom or molecule is defined as the amount of energy released when an electron attaches to a neutral atom or molecule in the gaseous state to form an anion.
::X(g) + e− → X−(g) + energy
Note that this is ...
into the Mulliken electronegativity, it is seen that the Mulliken chemical potential is a finite difference approximation of the electronic energy with respect to the number of electrons., i.e.,
:
Sub-nuclear particles
In recent years,thermal physics
Thermal physics is the combined study of thermodynamics, statistical mechanics, and kinetic theory of gases. This umbrella-subject is typically designed for physics students and functions to provide a general introduction to each of three core hea ...
has applied the definition of chemical potential to systems in particle physics
Particle physics or high energy physics is the study of fundamental particles and forces that constitute matter and radiation. The fundamental particles in the universe are classified in the Standard Model as fermions (matter particles) an ...
and its associated processes. For example, in a quark–gluon plasma
Quark–gluon plasma (QGP) or quark soup is an interacting localized assembly of quarks and gluons at thermal (local kinetic) and (close to) chemical (abundance) equilibrium. The word ''plasma'' signals that free color charges are allowed. In a ...
or other QCD matter
Quark matter or QCD matter (quantum chromodynamic) refers to any of a number of hypothetical phases of matter whose degrees of freedom include quarks and gluons, of which the prominent example is quark-gluon plasma. Several series of conferenc ...
, at every point in space there is a chemical potential for photon
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless, so they always ...
s, a chemical potential for electrons, a chemical potential for baryon number
In particle physics, the baryon number is a strictly conserved additive quantum number of a system. It is defined as
::B = \frac\left(n_\text - n_\bar\right),
where ''n''q is the number of quarks, and ''n'' is the number of antiquarks. Baryo ...
, electric charge
Electric charge is the physical property of matter that causes charged matter to experience a force when placed in an electromagnetic field. Electric charge can be ''positive'' or ''negative'' (commonly carried by protons and electrons respe ...
, and so forth.
In the case of photons, photons are boson
In particle physics, a boson ( ) is a subatomic particle whose spin quantum number has an integer value (0,1,2 ...). Bosons form one of the two fundamental classes of subatomic particle, the other being fermions, which have odd half-integer s ...
s and can very easily and rapidly appear or disappear. Therefore, at thermodynamic equilibrium, the chemical potential of photons is always and everywhere zero. The reason is, if the chemical potential somewhere was higher than zero, photons would spontaneously disappear from that area until the chemical potential went back to zero; likewise, if the chemical potential somewhere was less than zero, photons would spontaneously appear until the chemical potential went back to zero. Since this process occurs extremely rapidly (at least, it occurs rapidly in the presence of dense charged matter), it is safe to assume that the photon chemical potential is never different from zero.
Electric charge is different because it is conserved, i.e. it can be neither created nor destroyed. It can, however, diffuse. The "chemical potential of electric charge" controls this diffusion: Electric charge, like anything else, will tend to diffuse from areas of higher chemical potential to areas of lower chemical potential. Other conserved quantities like baryon number
In particle physics, the baryon number is a strictly conserved additive quantum number of a system. It is defined as
::B = \frac\left(n_\text - n_\bar\right),
where ''n''q is the number of quarks, and ''n'' is the number of antiquarks. Baryo ...
are the same. In fact, each conserved quantity is associated with a chemical potential and a corresponding tendency to diffuse to equalize it out.by Jean Letessier, Johann Rafelski, p. 91.
pair production
Pair production is the creation of a subatomic particle and its antiparticle from a neutral boson. Examples include creating an electron and a positron, a muon and an antimuon, or a proton and an antiproton. Pair production often refers specifi ...
), so the chemical potential of electrons by themselves becomes a less useful quantity than the chemical potential of the conserved quantities like (electrons minus positrons).
The chemical potentials of boson
In particle physics, a boson ( ) is a subatomic particle whose spin quantum number has an integer value (0,1,2 ...). Bosons form one of the two fundamental classes of subatomic particle, the other being fermions, which have odd half-integer s ...
s and fermion
In particle physics, a fermion is a particle that follows Fermi–Dirac statistics. Generally, it has a half-odd-integer spin: spin , spin , etc. In addition, these particles obey the Pauli exclusion principle. Fermions include all quarks an ...
s is related to the number of particles and the temperature by Bose–Einstein statistics
In quantum statistics, Bose–Einstein statistics (B–E statistics) describes one of two possible ways in which a collection of non-interacting, indistinguishable particles may occupy a set of available discrete energy states at thermodynamic ...
and Fermi–Dirac statistics respectively.
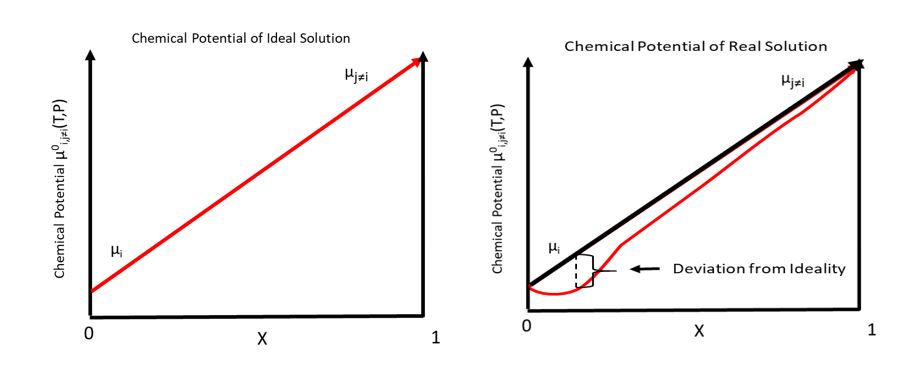
Ideal vs. non-ideal solutions
 Generally the chemical potential is given as a sum of an ideal contribution and an excess contribution:
:
In an ideal solution, the chemical potential of species ''i'' (μ''i'') is dependent on temperature and pressure.
μ''i''0(''T'', ''P'') is defined as the chemical potential of pure species ''i''. Given this definition, the chemical potential of species ''i'' in an ideal solution is
:
where ''R'' is the gas constant, and is the mole fraction of species ''i'' contained in the solution. The chemical potential becomes negative infinity when , but this does not lead to nonphysical results because means that species ''i'' is not present in the system.
This equation assumes that only depends on the mole fraction () contained in the solution. This neglects intermolecular interaction between species ''i'' with itself and other species 'i''–(''j''≠''i'') This can be corrected for by factoring in the coefficient of activity of species ''i'', defined as γ''i''. This correction yields
:
The plots above give a very rough picture of the ideal and non-ideal situation.
Generally the chemical potential is given as a sum of an ideal contribution and an excess contribution:
:
In an ideal solution, the chemical potential of species ''i'' (μ''i'') is dependent on temperature and pressure.
μ''i''0(''T'', ''P'') is defined as the chemical potential of pure species ''i''. Given this definition, the chemical potential of species ''i'' in an ideal solution is
:
where ''R'' is the gas constant, and is the mole fraction of species ''i'' contained in the solution. The chemical potential becomes negative infinity when , but this does not lead to nonphysical results because means that species ''i'' is not present in the system.
This equation assumes that only depends on the mole fraction () contained in the solution. This neglects intermolecular interaction between species ''i'' with itself and other species 'i''–(''j''≠''i'') This can be corrected for by factoring in the coefficient of activity of species ''i'', defined as γ''i''. This correction yields
:
The plots above give a very rough picture of the ideal and non-ideal situation.
See also
*Chemical equilibrium
In a chemical reaction, chemical equilibrium is the state in which both the Reagent, reactants and Product (chemistry), products are present in concentrations which have no further tendency to change with time, so that there is no observable chan ...
* Electrochemical potential
In electrochemistry, the electrochemical potential (ECP), ', is a thermodynamic measure of chemical potential that does not omit the energy contribution of electrostatics. Electrochemical potential is expressed in the unit of J/ mol.
Introductio ...
* Equilibrium chemistry
Equilibrium chemistry is concerned with systems in chemical equilibrium. The unifying principle is that the free energy of a system at equilibrium is the minimum possible, so that the slope of the free energy with respect to the reaction coordin ...
* Excess chemical potential
In thermodynamics, the excess chemical potential is defined as the difference between the chemical potential of a given species and that of an ideal gas under the same conditions (in particular, at the same pressure, temperature, and composition). ...
* Fugacity
In chemical thermodynamics, the fugacity of a real gas is an effective partial pressure which replaces the mechanical partial pressure in an accurate computation of the chemical equilibrium constant. It is equal to the pressure of an ideal gas whic ...
* Partial molar property
In thermodynamics, a partial molar property is a quantity which describes the variation of an extensive property of a solution or mixture with changes in the molar composition of the mixture at constant temperature and pressure. It is the part ...
* Thermodynamic activity
In chemical thermodynamics, activity (symbol ) is a measure of the "effective concentration" of a species in a mixture, in the sense that the species' chemical potential depends on the activity of a real solution in the same way that it would depe ...
* Thermodynamic equilibrium
Thermodynamic equilibrium is an axiomatic concept of thermodynamics. It is an internal state of a single thermodynamic system, or a relation between several thermodynamic systems connected by more or less permeable or impermeable walls. In the ...
References
External links
* G. Cook and R. H. Dickerson, "Understanding the chemical potential", American Journal of Physics 63, pp. 737–742 (1995), . * T. A. Kaplan, "The Chemical Potential", Journal of Statistical Physics 122, pp. 1237–1260 (2006), . * {{Authority control Physical chemistry Potentials Chemical thermodynamics Thermodynamic properties Chemical engineering thermodynamics