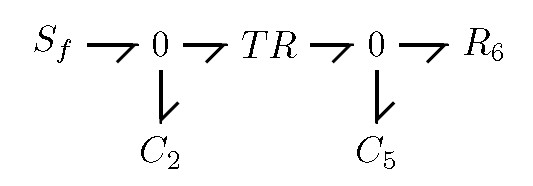
Bond graph on:
[Wikipedia]
[Google]
[Amazon]
 A bond graph is a graphical representation of a physical dynamic system. It allows the conversion of the system into a
A bond graph is a graphical representation of a physical dynamic system. It allows the conversion of the system into a
 The tetrahedron of state is a tetrahedron that graphically shows the conversion between effort and flow. The adjacent image shows the tetrahedron in its generalized form. The tetrahedron can be modified depending on the energy domain.
Using the tetrahedron of state, one can find a mathematical relationship between any variables on the tetrahedron. This is done by following the arrows around the diagram and multiplying any constants along the way. For example, if you wanted to find the relationship between generalized flow and generalized displacement, you would start at the and then integrate it to get . More examples of equations can be seen below.
Relationship between generalized displacement and generalized flow.
Relationship between generalized flow and generalized effort.
Relationship between generalized flow and generalized momentum.
Relationship between generalized momentum and generalized effort.
Relationship between generalized flow and generalized effort, involving the constant C.
All of the mathematical relationships remain the same when switching energy domains, only the symbols change. This can be seen with the following examples.
Relationship between displacement and velocity.
Relationship between current and voltage, this is also known as
The tetrahedron of state is a tetrahedron that graphically shows the conversion between effort and flow. The adjacent image shows the tetrahedron in its generalized form. The tetrahedron can be modified depending on the energy domain.
Using the tetrahedron of state, one can find a mathematical relationship between any variables on the tetrahedron. This is done by following the arrows around the diagram and multiplying any constants along the way. For example, if you wanted to find the relationship between generalized flow and generalized displacement, you would start at the and then integrate it to get . More examples of equations can be seen below.
Relationship between generalized displacement and generalized flow.
Relationship between generalized flow and generalized effort.
Relationship between generalized flow and generalized momentum.
Relationship between generalized momentum and generalized effort.
Relationship between generalized flow and generalized effort, involving the constant C.
All of the mathematical relationships remain the same when switching energy domains, only the symbols change. This can be seen with the following examples.
Relationship between displacement and velocity.
Relationship between current and voltage, this is also known as
 Parallel power can be simplified, by recalling the relationship between effort and flow for 0 and 1-junctions. To solve parallel power you will first want to write down all of the equations for the junctions. For the example provided, the equations can be seen below. (Please make note of the number bond the effort/flow variable represents).
By manipulating these equations you can arrange them such that you can find an equivalent set of 0 and 1-junctions to describe the parallel power.
For example, because and you can replace the variables in the equation resulting in and since , we now know that . This relationship of two effort variables equaling can be explained by an 0-junction. Manipulating other equations you can find that which describes the relationship of a 1-junction. Once you have determined the relationships that you need you can redraw the parallel power section with the new junctions. The result for the example show is seen below.
Parallel power can be simplified, by recalling the relationship between effort and flow for 0 and 1-junctions. To solve parallel power you will first want to write down all of the equations for the junctions. For the example provided, the equations can be seen below. (Please make note of the number bond the effort/flow variable represents).
By manipulating these equations you can arrange them such that you can find an equivalent set of 0 and 1-junctions to describe the parallel power.
For example, because and you can replace the variables in the equation resulting in and since , we now know that . This relationship of two effort variables equaling can be explained by an 0-junction. Manipulating other equations you can find that which describes the relationship of a 1-junction. Once you have determined the relationships that you need you can redraw the parallel power section with the new junctions. The result for the example show is seen below.
 The first step is to draw 0-junctions at all of the nodes:
The next step is to add all of the elements acting at their own 1-junction:
The next step is to pick a ground. The ground is simply an 0-junction that is going to be assumed to have no voltage. For this case, the ground will be chosen to be the lower left 0-junction, that is underlined above. The next step is to draw all of the arrows for the bond graph. The arrows on junctions should point towards ground (following a similar path to current). For resistance, inertance, and compliance elements, the arrows always point towards the elements. The result of drawing the arrows can be seen below, with the 0-junction marked with a star as the ground.
The first step is to draw 0-junctions at all of the nodes:
The next step is to add all of the elements acting at their own 1-junction:
The next step is to pick a ground. The ground is simply an 0-junction that is going to be assumed to have no voltage. For this case, the ground will be chosen to be the lower left 0-junction, that is underlined above. The next step is to draw all of the arrows for the bond graph. The arrows on junctions should point towards ground (following a similar path to current). For resistance, inertance, and compliance elements, the arrows always point towards the elements. The result of drawing the arrows can be seen below, with the 0-junction marked with a star as the ground.
 Now that we have the Bond graph, we can start the process of simplifying it. The first step is to remove all the ground nodes. Both of the bottom 0-junctions can be removed, because they are both grounded. The result is shown below.
Now that we have the Bond graph, we can start the process of simplifying it. The first step is to remove all the ground nodes. Both of the bottom 0-junctions can be removed, because they are both grounded. The result is shown below.
 Next, the junctions with less than three bonds can be removed. This is because flow and effort pass through these junctions without being modified, so they can be removed to allow us to draw less. The result can be seen below.
Next, the junctions with less than three bonds can be removed. This is because flow and effort pass through these junctions without being modified, so they can be removed to allow us to draw less. The result can be seen below.
 The final step is to apply causality to the bond graph. Applying causality was explained above. The final bond graph is shown below.
The final step is to apply causality to the bond graph. Applying causality was explained above. The final bond graph is shown below.

 Following the steps with this circuit will result in the bond graph below, before it is simplified. The nodes marked with the star denote the ground.
Following the steps with this circuit will result in the bond graph below, before it is simplified. The nodes marked with the star denote the ground.
 Simplifying the bond graph will result in the image below.
Simplifying the bond graph will result in the image below.
 Lastly, applying causality will result in the bond graph below. The bond with star denotes a causal conflict.
Lastly, applying causality will result in the bond graph below. The bond with star denotes a causal conflict.

 For a mechanical system, the first step is to place a 1-junction at each distinct velocity, in this case there are two distinct velocities, the mass and the wall. It is usually helpful to label the 1-junctions for reference. The result is below.
The next step is to draw the R and C bonds at their own 0-junctions between the 1-junctions where they act. For this example there is only one of these bonds, the C bond for the spring. It acts between the 1-junction representing the mass and the 1-junction representing the wall. The result is below.
Next you want to add the sources and I bonds on the 1-junction where they act. There is one source, the source of effort (force) and one I bond, the mass of the mass both of which act on the 1-junction of the mass. The result is shown below.
Next power flow is to be assigned. Like the electrical examples, power should flow towards ground, in this case the 1-junction of the wall. Exceptions to this are R,C, or I bond, which always point towards the element. The resulting bond graph is below.
For a mechanical system, the first step is to place a 1-junction at each distinct velocity, in this case there are two distinct velocities, the mass and the wall. It is usually helpful to label the 1-junctions for reference. The result is below.
The next step is to draw the R and C bonds at their own 0-junctions between the 1-junctions where they act. For this example there is only one of these bonds, the C bond for the spring. It acts between the 1-junction representing the mass and the 1-junction representing the wall. The result is below.
Next you want to add the sources and I bonds on the 1-junction where they act. There is one source, the source of effort (force) and one I bond, the mass of the mass both of which act on the 1-junction of the mass. The result is shown below.
Next power flow is to be assigned. Like the electrical examples, power should flow towards ground, in this case the 1-junction of the wall. Exceptions to this are R,C, or I bond, which always point towards the element. The resulting bond graph is below.
 Now that the bond graph has been generated, it can be simplified. Because the wall is grounded (has zero velocity), you can remove that junction. As such the 0-junction the C bond is on, can also be removed because it will then have less than three bonds. The simplified bond graph can be seen below.
Now that the bond graph has been generated, it can be simplified. Because the wall is grounded (has zero velocity), you can remove that junction. As such the 0-junction the C bond is on, can also be removed because it will then have less than three bonds. The simplified bond graph can be seen below.
 The last step is to apply causality, the final bond graph can be seen below.
The last step is to apply causality, the final bond graph can be seen below.

 Just like the above example, the first step is to make 1-junctions at each of the distant velocities. In this example there are three distant velocity, Mass 1, Mass 2, and the wall. Then you connect all of the bonds and assign power flow. The bond can be seen below.
Just like the above example, the first step is to make 1-junctions at each of the distant velocities. In this example there are three distant velocity, Mass 1, Mass 2, and the wall. Then you connect all of the bonds and assign power flow. The bond can be seen below.
 Next you start the process of simplifying the bond graph, by removing the 1-junction of the wall, and removing junctions with less than three bonds. The bond graph can be seen below.
Next you start the process of simplifying the bond graph, by removing the 1-junction of the wall, and removing junctions with less than three bonds. The bond graph can be seen below.
 There is parallel power in the bond graph. Solving parallel power was explained above. The result of solving it can be seen below.
There is parallel power in the bond graph. Solving parallel power was explained above. The result of solving it can be seen below.
 Lastly, apply causality, the final bond graph can be seen below.
Lastly, apply causality, the final bond graph can be seen below.

 you would have the following , , and matrices:
The matrices of and are solved by determining the relationship of the state variables and their respective elements, as was described in the tetrahedron of state. The first step to solve the state equations is to list all of the governing equations for the bond graph. The table below shows the relationship between bonds and their governing equations.
"♦" denotes preferred causality.
For the example provided,
you would have the following , , and matrices:
The matrices of and are solved by determining the relationship of the state variables and their respective elements, as was described in the tetrahedron of state. The first step to solve the state equations is to list all of the governing equations for the bond graph. The table below shows the relationship between bonds and their governing equations.
"♦" denotes preferred causality.
For the example provided,
 the governing equations are the following.
#
#
#
#
#
#
#
#
#
#
#
These equations can be manipulated to yield the state equations. For this example, you are trying to find equations that relate and in terms of , , and .
To start you should recall from the tetrahedron of state that starting with equation 2, you can rearrange it so that . can be substituted for equation 4, while in equation 4, can be replaced by due to equation 3, which can then be replaced by equation 5. can likewise be replaced using equation 7, in which can be replaced with which can then be replaced with equation 10. Following these substituted yields the first state equation which is shown below.
The second state equation can likewise be solved, by recalling that . The second state equation is shown below.
Both equations can further be rearranged into matrix form. The result of which is below.
At this point the equations can be treated as any other
the governing equations are the following.
#
#
#
#
#
#
#
#
#
#
#
These equations can be manipulated to yield the state equations. For this example, you are trying to find equations that relate and in terms of , , and .
To start you should recall from the tetrahedron of state that starting with equation 2, you can rearrange it so that . can be substituted for equation 4, while in equation 4, can be replaced by due to equation 3, which can then be replaced by equation 5. can likewise be replaced using equation 7, in which can be replaced with which can then be replaced with equation 10. Following these substituted yields the first state equation which is shown below.
The second state equation can likewise be solved, by recalling that . The second state equation is shown below.
Both equations can further be rearranged into matrix form. The result of which is below.
At this point the equations can be treated as any other
ECMS-2013 27th European Conference on Modelling and Simulation, May 27–30, 2013, Ålesund, Norway
* [https://web.archive.org/web/20070125062943/http://www.scs.org/confernc/wmc/wmc07/icbgm07_FinalProgram_2.PDF ICBGM-2007: 8th International Conference on Bond Graph Modeling And Simulation, January 15–17, 2007, San Diego, California, U.S.A.]
ECMS-2006 20TH European Conference on Modelling and Simulation, May 28–31, 2006, Bonn, Germany
* ttp://gaia.csus.edu/~grandajj/icbgm05_FinalProgram.htm ICBGM-2005 International Conference on Bond Graph Modeling and Simulation, January 23–27, 2005, New Orleans, Louisiana, U.S.A.�
Papers
– ttps://web.archive.org/web/20080414235710/http://www.scs.org/search.cfm?presearch=db&dbrec=15 Papers
14TH European Simulation symposium October 23–26, 2002 Dresden, Germany
* ttp://gaia.csus.edu/~grandajj/WMC2001-ICBGM.htm ICBGM-2001 International Conference on Bond Graph Modeling and Simulation (ICBGM 2001), Phoenix, Arizona U.S.A.
European Simulation Multi-conference 23-26 May, 2000, Gent, Belgium
* [https://web.archive.org/web/20080408105504/http://www-control.eng.cam.ac.uk/extras/conferences/ICBGM99 ICBGM-1999 International Conference on Bond Graph Modeling and Simulation January 17–20, 1999 San Francisco, California]
ESS-97 9TH European Simulation Symposium and Exhibition Simulation in Industry, Passau, Germany, October 19–22, 1997
* ttp://www.scs-europe.net/conf/esm97/fintue.html 11th European Simulation Multiconference Istanbul, Turkey, June 1–4, 1997
ESM-1996 10th annual European Simulation Multiconference Budapest, Hungary, June 2–6, 1996
* ICBGM-1995 Int. Conf. on Bond Graph Modeling and Simulation (ICBGM’95), January 15–18, 1995,Las Vegas, Nevada.
Simscape
Official MATLAB/Simulink add-on library for graphical bond graph programming
Freeware MATLAB/Simulink add-on library for graphical bond graph programming Scientific visualization Diagrams Application-specific graphs Electrical engineering Mechanical engineering Modeling languages
 A bond graph is a graphical representation of a physical dynamic system. It allows the conversion of the system into a
A bond graph is a graphical representation of a physical dynamic system. It allows the conversion of the system into a state-space representation
In control engineering, a state-space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations or difference equations. State variables are variables ...
. It is similar to a block diagram
A block diagram is a diagram of a system in which the principal parts or functions are represented by blocks connected by lines that show the relationships of the blocks.
or signal-flow graph
A signal-flow graph or signal-flowgraph (SFG), invented by Claude Shannon, but often called a Mason graph after Samuel Jefferson Mason who coined the term, is a specialized flow graph, a directed graph in which nodes represent system variables, ...
, with the major difference that the arcs in bond graphs represent bi-directional exchange of physical energy
In physics, energy (from Ancient Greek: ἐνέργεια, ''enérgeia'', “activity”) is the quantitative property that is transferred to a body or to a physical system, recognizable in the performance of work and in the form of ...
, while those in block diagrams and signal-flow graphs represent uni-directional flow of information. Bond graphs are multi-energy domain (e.g. mechanical, electrical, hydraulic, etc.) and domain neutral. This means a bond graph can incorporate multiple domains seamlessly.
The bond graph is composed of the "bonds" which link together "single-port", "double-port" and "multi-port" elements (see below for details). Each bond represents the instantaneous flow of energy (''dE''/''dt'') or power
Power most often refers to:
* Power (physics), meaning "rate of doing work"
** Engine power, the power put out by an engine
** Electric power
* Power (social and political), the ability to influence people or events
** Abusive power
Power may a ...
. The flow in each bond is denoted by a pair of variables called power variables, akin to conjugate variables
Conjugate variables are pairs of variables mathematically defined in such a way that they become Fourier transform duals, or more generally are related through Pontryagin duality. The duality relations lead naturally to an uncertainty relation� ...
, whose product is the instantaneous power of the bond. The power variables are broken into two parts: ''flow'' and ''effort''. For example, for the bond of an electrical system, the flow is the current, while the effort is the voltage. By multiplying current and voltage in this example you can get the instantaneous power of the bond.
A bond has two other features described briefly here, and discussed in more detail below. One is the "half-arrow" sign convention. This defines the assumed direction of positive energy flow. As with electrical circuit diagrams and free-body diagrams, the choice of positive direction is arbitrary, with the caveat that the analyst must be consistent throughout with the chosen definition. The other feature is the "causality". This is a vertical bar placed on only one end of the bond. It is not arbitrary. As described below, there are rules for assigning the proper causality to a given port, and rules for the precedence among ports. Causality explains the mathematical relationship between effort and flow. The positions of the causalities show which of the power variables are dependent and which are independent.
If the dynamics of the physical system to be modeled operate on widely varying time scales, fast continuous-time behaviors can be modeled as instantaneous phenomena by using a hybrid bond graph. Bond graphs were invented by Henry Paynter.
Systems for bond graph
Many systems can be expressed in terms used in bond graph. These terms are expressed in the table below. Conventions for the table below: * is theactive power
Active may refer to:
Music
* ''Active'' (album), a 1992 album by Casiopea
* Active Records, a record label
Ships
* ''Active'' (ship), several commercial ships by that name
* HMS ''Active'', the name of various ships of the British Royal ...
;
* is a matrix
Matrix most commonly refers to:
* ''The Matrix'' (franchise), an American media franchise
** '' The Matrix'', a 1999 science-fiction action film
** "The Matrix", a fictional setting, a virtual reality environment, within ''The Matrix'' (franchi ...
object;
* is a vector
Vector most often refers to:
*Euclidean vector, a quantity with a magnitude and a direction
*Vector (epidemiology), an agent that carries and transmits an infectious pathogen into another living organism
Vector may also refer to:
Mathematic ...
object;
* is the Hermitian {{Short description, none
Numerous things are named after the French mathematician Charles Hermite (1822–1901):
Hermite
* Cubic Hermite spline, a type of third-degree spline
* Gauss–Hermite quadrature, an extension of Gaussian quadrature m ...
of ; it is the complex conjugate
In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign. That is, (if a and b are real, then) the complex conjugate of a + bi is equal to a - ...
of the transpose
In linear algebra, the transpose of a matrix is an operator which flips a matrix over its diagonal;
that is, it switches the row and column indices of the matrix by producing another matrix, often denoted by (among other notations).
The tr ...
of . If is a scalar, then the Hermitian is the same as the complex conjugate;
* is the Euler notation for differentiation, where:
*
*Vergent-factor:
Other systems:
* Thermodynamic power system (flow is entropy-rate and effort is temperature)
* Electrochemical power system (flow is chemical activity and effort is chemical potential)
* Thermochemical power system (flow is mass-rate and effort is mass specific enthalpy)
* Macroeconomics currency-rate system (displacement is commodity and effort is price per commodity)
* Microeconomics currency-rate system (displacement is population and effort is GDP per capita)
Tetrahedron of state
 The tetrahedron of state is a tetrahedron that graphically shows the conversion between effort and flow. The adjacent image shows the tetrahedron in its generalized form. The tetrahedron can be modified depending on the energy domain.
Using the tetrahedron of state, one can find a mathematical relationship between any variables on the tetrahedron. This is done by following the arrows around the diagram and multiplying any constants along the way. For example, if you wanted to find the relationship between generalized flow and generalized displacement, you would start at the and then integrate it to get . More examples of equations can be seen below.
Relationship between generalized displacement and generalized flow.
Relationship between generalized flow and generalized effort.
Relationship between generalized flow and generalized momentum.
Relationship between generalized momentum and generalized effort.
Relationship between generalized flow and generalized effort, involving the constant C.
All of the mathematical relationships remain the same when switching energy domains, only the symbols change. This can be seen with the following examples.
Relationship between displacement and velocity.
Relationship between current and voltage, this is also known as
The tetrahedron of state is a tetrahedron that graphically shows the conversion between effort and flow. The adjacent image shows the tetrahedron in its generalized form. The tetrahedron can be modified depending on the energy domain.
Using the tetrahedron of state, one can find a mathematical relationship between any variables on the tetrahedron. This is done by following the arrows around the diagram and multiplying any constants along the way. For example, if you wanted to find the relationship between generalized flow and generalized displacement, you would start at the and then integrate it to get . More examples of equations can be seen below.
Relationship between generalized displacement and generalized flow.
Relationship between generalized flow and generalized effort.
Relationship between generalized flow and generalized momentum.
Relationship between generalized momentum and generalized effort.
Relationship between generalized flow and generalized effort, involving the constant C.
All of the mathematical relationships remain the same when switching energy domains, only the symbols change. This can be seen with the following examples.
Relationship between displacement and velocity.
Relationship between current and voltage, this is also known as Ohm's law
Ohm's law states that the current through a conductor between two points is directly proportional to the voltage across the two points. Introducing the constant of proportionality, the resistance, one arrives at the usual mathematical equa ...
.
Relationship between force and displacement, also known as Hooke's law
In physics, Hooke's law is an empirical law which states that the force () needed to extend or compress a spring by some distance () scales linearly with respect to that distance—that is, where is a constant factor characteristic of t ...
. The negative sign is dropped in this equation because the sign is factored into the way the arrow is pointing in the bond graph.
For power systems, the formula for the frequency of resonance is as follows:
For power density systems, the formula for the velocity of the resonance wave is as follows:
Components
If an engine is connected to a wheel through a shaft, the power is being transmitted in the rotational mechanical domain, meaning the effort and the flow are torque (τ) and angular velocity (ω) respectively. A word bond graph is a first step towards a bond graph, in which words define the components. As a word bond graph, this system would look like: A half-arrow is used to provide a sign convention, so if the engine is doing work when ''τ'' and ''ω'' are positive, then the diagram would be drawn: This system can also be represented in a more general method. This involves changing from using the words, to symbols representing the same items. These symbols are based on the generalized form, as explained above. As the engine is applying a torque to the wheel, it will be represented as a source of effort for the system. The wheel can be presented by an impedance on the system. Further, the torque and angular velocity symbols are dropped and replaced with the generalized symbols for effort and flow. While not necessary in the example, it is common to number the bonds, to keep track of in equations. The simplified diagram can be seen below. Given that effort is always above the flow on the bond, it is also possible to drop the effort and flow symbols altogether, without losing any relevant information. However, the bond number should not be dropped. The example can be seen below. The bond number will be important later when converting from the bond graph to state-space equations.Association of elements
Series association
Suppose that an element has the following behavior: where is a generic function (it can even differentiate/integrate its input) and is the element's constant. Then, suppose that in a 1-junction you have many of this type of element. Then the total voltage across the junction is:Parallel association
Suppose that an element has the following behavior: where is a generic function (it can even differentiate/integrate its input) and is the element's constant. Then, suppose that in a 0-junction you have many of this type of element. Then it is valid:Single-port elements
Single-port elements are elements in a bond graph that can have only one port.Sources and sinks
Sources are elements that represent the input for a system. They will either input effort or flow into a system. They are denoted by a capital "S" with either a lower case "e" or "f" for effort or flow respectively. Sources will always have the arrow pointing away from the element. Examples of sources include: motors (source of effort, torque), voltage sources (source of effort), and current sources (source of flow). where ''J'' indicates a junction. Sinks are elements that represent the output for a system. They are represented the same way as sources, but have the arrow pointing into the element instead of away from it.Inertia
Inertia elements are denoted by a capital "I", and always have power flowing into them. Inertia elements are elements that store energy. Most commonly these are a mass for mechanical systems, and inductors for electrical systems.Resistance
Resistance elements are denoted by a capital "R", and always have power flowing into them. Resistance elements are elements that dissipate energy. Most commonly these are a damper, for mechanical systems, and resistors for electrical systems.Compliance
Compliance elements are denoted by a capital "C", and always have power flowing into them. Compliance elements are elements that store potential energy. Most commonly these are springs for mechanical systems, and capacitors for electrical systems.Two-port elements
These elements have two ports. They are used to change the power between or within a system. When converting from one to the other, no power is lost during the transfer. The elements have a constant that will be given with it. The constant is called a transformer constant or gyrator constant depending on which element is being used. These constants will commonly be displayed as a ratio below the element.Transformer
A transformer applies a relationship between flow in flow out, and effort in effort out. Examples include an ideal electricaltransformer
A transformer is a passive component that transfers electrical energy from one electrical circuit to another circuit, or multiple circuits. A varying current in any coil of the transformer produces a varying magnetic flux in the transformer' ...
or a lever
A lever is a simple machine consisting of a beam or rigid rod pivoted at a fixed hinge, or '' fulcrum''. A lever is a rigid body capable of rotating on a point on itself. On the basis of the locations of fulcrum, load and effort, the lever is d ...
.
Denoted
where the ''r'' denotes the modulus of the transformer. This means
and
Gyrator
Agyrator
A gyrator is a passive, linear, lossless, two-port electrical network element proposed in 1948 by Bernard D. H. Tellegen as a hypothetical fifth linear element after the resistor, capacitor, inductor and ideal transformer. Unlike the four conv ...
applies a relationship between flow in effort out, and effort in flow out. An example of a gyrator is a DC motor, which converts voltage (electrical effort) into angular velocity (angular mechanical flow).
meaning that and
Multi-port elements
Junctions, unlike the other elements can have any number of ports either in or out. Junctions split power across their ports. There are two distinct junctions, the 0-junction and the 1-junction which differ only in how effort and flow are carried across. The same junction in series can be combined, but different junctions in series cannot.0-junctions
0-junctions behave such that all effort values (and its time integral/derivative) are equal across the bonds, but the sum of the flow values in equals the sum of the flow values out, or equivalently, all flows sum to zero. In an electrical circuit, the 0-junction is a node and represents a voltage shared by all components at that node. In a mechanical circuit, the 0-junction is a joint among components, and represents a force shared by all components connected to it. An example is shown below. Resulting equations:1-junctions
1-junctions behave opposite of 0-junctions. 1-junctions behave such that all flow values (and its time integral/derivative) are equal across the bonds, but the sum of the effort values in equals the sum the effort values out, or equivalently, all efforts sum to zero. In an electrical circuit, the 1 junction represents a series connection among components. In a mechanical circuit, the 1-junction represents a velocity shared by all components connected to it. An example is shown below. Resulting equations:Causality
Bond graphs have a notion of causality, indicating which side of a bond determines the instantaneous effort and which determines the instantaneous flow. In formulating the dynamic equations that describe the system, causality defines, for each modeling element, which variable is dependent and which is independent. By propagating the causation graphically from one modeling element to the other, analysis of large-scale models becomes easier. Completing causal assignment in a bond graph model will allow the detection of modeling situation where an algebraic loop exists; that is the situation when a variable is defined recursively as a function of itself. As an example of causality, consider a capacitor in series with a battery. It is not physically possible to charge a capacitor instantly, so anything connected in parallel with a capacitor will necessarily have the same voltage (effort variable) as that across the capacitor. Similarly, an inductor cannot change flux instantly and so any component in series with an inductor will necessarily have the same flow as the inductor. Because capacitors and inductors are passive devices, they cannot maintain their respective voltage and flow indefinitely—the components to which they are attached will affect their respective voltage and flow, but only indirectly by affecting their current and voltage respectively. Note: Causality is a symmetric relationship. When one side "causes" effort, the other side "causes" flow. In bond graph notation, a causal stroke may be added to one end of the power bond to indicate that this side is defining the ''flow''. Consequently, the side opposite from the casual stroke controls the ''effort''. Sources of flow () define flow, so they host the causal stroke: Sources of effort () define effort, so the other end hosts the causal stroke: Consider a constant-torque motor driving a wheel, i.e. a source of effort (). That would be drawn as follows: Symmetrically, the side with the causal stroke (in this case the wheel) defines the flow for the bond. Causality results in compatibility constraints. Clearly only one end of a power bond can define the effort and so only one end of a bond can (the other end) have a causal stroke. In addition, the two passive components with time-dependent behavior, and , can only have one sort of causation: an component determines flow; a component defines effort. So from a junction, , the preferred causal orientation is as follows: The reason that this is the preferred method for these elements can be further analyzed if you consider the equations they would give shown by the tetrahedron of state. The resulting equations involve the integral of the independent power variable. This is preferred over the result of having the causality the other way, which results in derivative. The equations can be seen below. It is possible for a bond graph to have a causal bar on one of these elements in the non-preferred manner. In such a case a "causal conflict" is said to have occurred at that bond. The results of a causal conflict are only seen when writing the state-space equations for the graph. It is explained in more details in that section. A resistor has no time-dependent behavior: apply a voltage and get a flow instantly, or apply a flow and get a voltage instantly, thus a resistor can be at either end of a causal bond: Transformers are passive, neither dissipating nor storing energy, so causality passes through them: A gyrator transforms flow to effort and effort to flow, so if flow is caused on one side, effort is caused on the other side and vice versa:Junctions
In a 0-junction, efforts are equal; in a 1-junction, flows are equal. Thus, with causal bonds, only one bond can cause the effort in a 0-junction and only one can cause the flow in a 1-junction. Thus, if the causality of one bond of a junction is known, the causality of the others is also known. That one bond is called the 'strong bond' In a nutshell, 0-junctions must have a single causal bar, 1-junctions must have all but one causal bars.Determining causality
In order to determine the causality of a bond graph certain steps must be followed. Those steps are: # Draw Source Causal Bars # Draw Preferred causality for C and I bonds # Draw causal bars for 0 and 1 junctions, transformers and gyrators # Draw R bond causal bars # If a causal conflict occurs, change C or I bond to differentiation A walk-through of the steps is shown below. The first step is to draw causality for the sources, over which there is only one. This results in the graph below. The next step is to draw the preferred causality for the C bonds. Next apply the causality for the 0 and 1 junctions, transformers, and gyrators. However, there is an issue with 0-junction on the left. The 0-junction has two causal bars at the junction, but the 0-junction wants one and only one at the junction. This was caused by having be in the preferred causality. The only way to fix this is to flip that causal bar. This results in a causal conflict, the corrected version of the graph is below, with the representing the causal conflict.Converting from other systems
One of the main advantages of using bond graphs is that once you have a bond graph it doesn't matter the original energy domain. Below are some of the steps to apply when converting from the energy domain to a bond graph.Electromagnetic
The steps for solving an Electromagnetic problem as a bond graph are as follows: # Place an 0-junction at each node # Insert Sources, R, I, C, TR, and GY bonds with 1 junctions # Ground (both sides if a transformer or gyrator is present) # Assign power flow direction # Simplify These steps are shown more clearly in the examples below.Linear mechanical
The steps for solving a Linear Mechanical problem as a bond graph are as follows: # Place 1-junctions for each distinct velocity (usually at a mass) # Insert R and C bonds at their own 0-junctions between the 1 junctions where they act # Insert Sources and I bonds on the 1 junctions where they act # Assign power flow direction # Simplify These steps are shown more clearly in the examples below.Simplifying
The simplifying step is the same regardless if the system was electromagnetic or linear mechanical. The steps are: # Remove Bond of zero power (due to ground or zero velocity) # Remove 0 and 1 junctions with less than three bonds # Simplify parallel power # Combine 0 junctions in series # Combine 1 junctions in series These steps are shown more clearly in the examples below.Parallel power
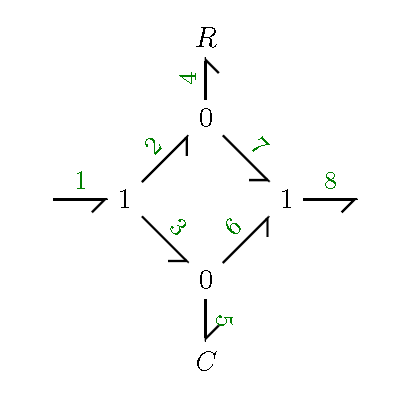
Parallel power is when power runs in parallel in a bond graph. An example of parallel power is shown below. Parallel power can be simplified, by recalling the relationship between effort and flow for 0 and 1-junctions. To solve parallel power you will first want to write down all of the equations for the junctions. For the example provided, the equations can be seen below. (Please make note of the number bond the effort/flow variable represents).
By manipulating these equations you can arrange them such that you can find an equivalent set of 0 and 1-junctions to describe the parallel power.
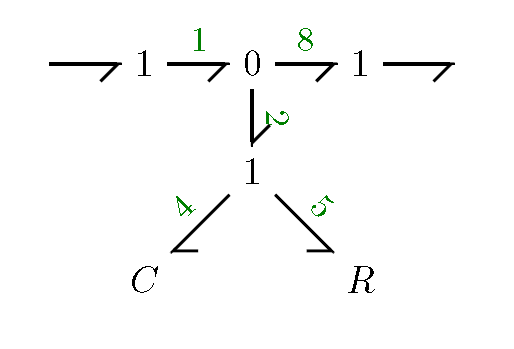
For example, because and you can replace the variables in the equation resulting in and since , we now know that . This relationship of two effort variables equaling can be explained by an 0-junction. Manipulating other equations you can find that which describes the relationship of a 1-junction. Once you have determined the relationships that you need you can redraw the parallel power section with the new junctions. The result for the example show is seen below.
Parallel power can be simplified, by recalling the relationship between effort and flow for 0 and 1-junctions. To solve parallel power you will first want to write down all of the equations for the junctions. For the example provided, the equations can be seen below. (Please make note of the number bond the effort/flow variable represents).
By manipulating these equations you can arrange them such that you can find an equivalent set of 0 and 1-junctions to describe the parallel power.
For example, because and you can replace the variables in the equation resulting in and since , we now know that . This relationship of two effort variables equaling can be explained by an 0-junction. Manipulating other equations you can find that which describes the relationship of a 1-junction. Once you have determined the relationships that you need you can redraw the parallel power section with the new junctions. The result for the example show is seen below.

Examples
Simple electrical system
A simple electrical circuit consisting of a voltage source, resistor, and capacitor in series. The first step is to draw 0-junctions at all of the nodes:
The next step is to add all of the elements acting at their own 1-junction:
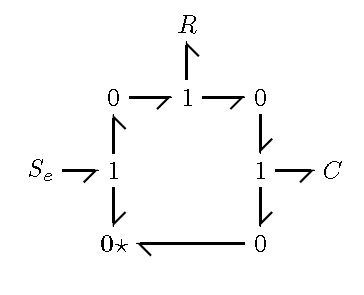
The next step is to pick a ground. The ground is simply an 0-junction that is going to be assumed to have no voltage. For this case, the ground will be chosen to be the lower left 0-junction, that is underlined above. The next step is to draw all of the arrows for the bond graph. The arrows on junctions should point towards ground (following a similar path to current). For resistance, inertance, and compliance elements, the arrows always point towards the elements. The result of drawing the arrows can be seen below, with the 0-junction marked with a star as the ground.
The first step is to draw 0-junctions at all of the nodes:
The next step is to add all of the elements acting at their own 1-junction:
The next step is to pick a ground. The ground is simply an 0-junction that is going to be assumed to have no voltage. For this case, the ground will be chosen to be the lower left 0-junction, that is underlined above. The next step is to draw all of the arrows for the bond graph. The arrows on junctions should point towards ground (following a similar path to current). For resistance, inertance, and compliance elements, the arrows always point towards the elements. The result of drawing the arrows can be seen below, with the 0-junction marked with a star as the ground.
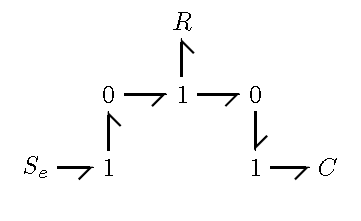
 Now that we have the Bond graph, we can start the process of simplifying it. The first step is to remove all the ground nodes. Both of the bottom 0-junctions can be removed, because they are both grounded. The result is shown below.
Now that we have the Bond graph, we can start the process of simplifying it. The first step is to remove all the ground nodes. Both of the bottom 0-junctions can be removed, because they are both grounded. The result is shown below.
 Next, the junctions with less than three bonds can be removed. This is because flow and effort pass through these junctions without being modified, so they can be removed to allow us to draw less. The result can be seen below.
Next, the junctions with less than three bonds can be removed. This is because flow and effort pass through these junctions without being modified, so they can be removed to allow us to draw less. The result can be seen below.
 The final step is to apply causality to the bond graph. Applying causality was explained above. The final bond graph is shown below.
The final step is to apply causality to the bond graph. Applying causality was explained above. The final bond graph is shown below.

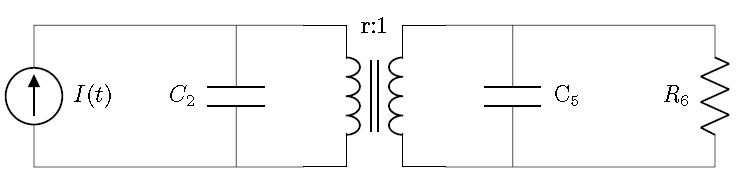
Advanced electrical system
A more advanced electrical system with a current source, resistors, capacitors, and a transformer Following the steps with this circuit will result in the bond graph below, before it is simplified. The nodes marked with the star denote the ground.
Following the steps with this circuit will result in the bond graph below, before it is simplified. The nodes marked with the star denote the ground.
 Simplifying the bond graph will result in the image below.
Simplifying the bond graph will result in the image below.
 Lastly, applying causality will result in the bond graph below. The bond with star denotes a causal conflict.
Lastly, applying causality will result in the bond graph below. The bond with star denotes a causal conflict.

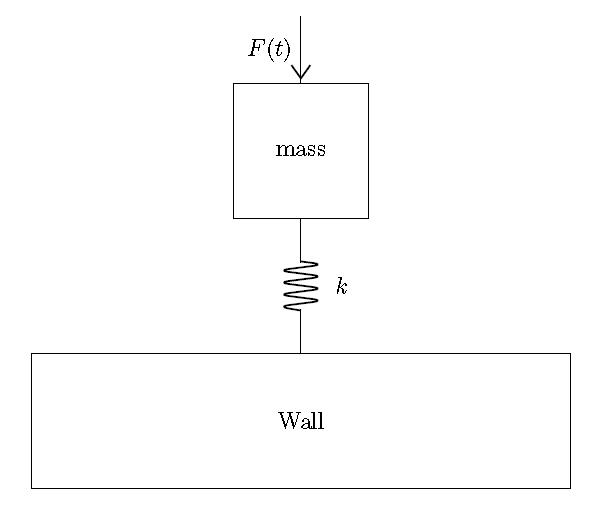
Simple linear mechanical
A simple linear mechanical system, consisting of a mass on a spring that is attached to a wall. The mass has some force being applied to it. An image of the system is shown below. For a mechanical system, the first step is to place a 1-junction at each distinct velocity, in this case there are two distinct velocities, the mass and the wall. It is usually helpful to label the 1-junctions for reference. The result is below.
The next step is to draw the R and C bonds at their own 0-junctions between the 1-junctions where they act. For this example there is only one of these bonds, the C bond for the spring. It acts between the 1-junction representing the mass and the 1-junction representing the wall. The result is below.
Next you want to add the sources and I bonds on the 1-junction where they act. There is one source, the source of effort (force) and one I bond, the mass of the mass both of which act on the 1-junction of the mass. The result is shown below.
Next power flow is to be assigned. Like the electrical examples, power should flow towards ground, in this case the 1-junction of the wall. Exceptions to this are R,C, or I bond, which always point towards the element. The resulting bond graph is below.
For a mechanical system, the first step is to place a 1-junction at each distinct velocity, in this case there are two distinct velocities, the mass and the wall. It is usually helpful to label the 1-junctions for reference. The result is below.
The next step is to draw the R and C bonds at their own 0-junctions between the 1-junctions where they act. For this example there is only one of these bonds, the C bond for the spring. It acts between the 1-junction representing the mass and the 1-junction representing the wall. The result is below.
Next you want to add the sources and I bonds on the 1-junction where they act. There is one source, the source of effort (force) and one I bond, the mass of the mass both of which act on the 1-junction of the mass. The result is shown below.
Next power flow is to be assigned. Like the electrical examples, power should flow towards ground, in this case the 1-junction of the wall. Exceptions to this are R,C, or I bond, which always point towards the element. The resulting bond graph is below.
 Now that the bond graph has been generated, it can be simplified. Because the wall is grounded (has zero velocity), you can remove that junction. As such the 0-junction the C bond is on, can also be removed because it will then have less than three bonds. The simplified bond graph can be seen below.
Now that the bond graph has been generated, it can be simplified. Because the wall is grounded (has zero velocity), you can remove that junction. As such the 0-junction the C bond is on, can also be removed because it will then have less than three bonds. The simplified bond graph can be seen below.
 The last step is to apply causality, the final bond graph can be seen below.
The last step is to apply causality, the final bond graph can be seen below.

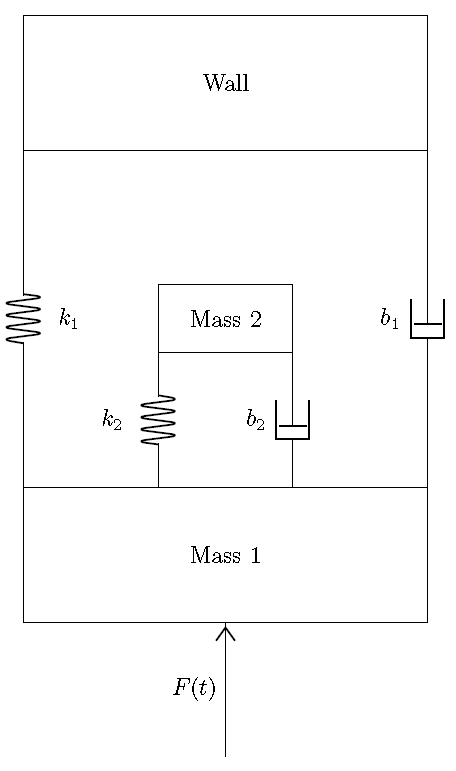
Advanced linear mechanical
A more advanced linear mechanical system can be seen below. Just like the above example, the first step is to make 1-junctions at each of the distant velocities. In this example there are three distant velocity, Mass 1, Mass 2, and the wall. Then you connect all of the bonds and assign power flow. The bond can be seen below.
Just like the above example, the first step is to make 1-junctions at each of the distant velocities. In this example there are three distant velocity, Mass 1, Mass 2, and the wall. Then you connect all of the bonds and assign power flow. The bond can be seen below.
 Next you start the process of simplifying the bond graph, by removing the 1-junction of the wall, and removing junctions with less than three bonds. The bond graph can be seen below.
Next you start the process of simplifying the bond graph, by removing the 1-junction of the wall, and removing junctions with less than three bonds. The bond graph can be seen below.
 There is parallel power in the bond graph. Solving parallel power was explained above. The result of solving it can be seen below.
There is parallel power in the bond graph. Solving parallel power was explained above. The result of solving it can be seen below.
 Lastly, apply causality, the final bond graph can be seen below.
Lastly, apply causality, the final bond graph can be seen below.

State equations
Once a bond graph is complete, it can be utilized to generate thestate-space representation
In control engineering, a state-space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations or difference equations. State variables are variables ...
equations of the system. State-space representation is especially powerful as it allows complex multi-order differential system to be solved as a system of first-order equations instead. The general form of the state equation is
where is a column matrix of the state variable
A state variable is one of the set of variables that are used to describe the mathematical "state" of a dynamical system. Intuitively, the state of a system describes enough about the system to determine its future behaviour in the absence of a ...
s, or the unknowns of the system. is the time derivative
A time derivative is a derivative of a function with respect to time, usually interpreted as the rate of change of the value of the function. The variable denoting time is usually written as t.
Notation
A variety of notations are used to denote th ...
of the state variables. is a column matrix of the inputs of the system. And and are matrices of constants based on the system. The state variables of a system are and values for each C and I bond without a causal conflict. Each I bond gets a while each C bond gets a .
For example, if you have the following bond graph
 you would have the following , , and matrices:
The matrices of and are solved by determining the relationship of the state variables and their respective elements, as was described in the tetrahedron of state. The first step to solve the state equations is to list all of the governing equations for the bond graph. The table below shows the relationship between bonds and their governing equations.
"♦" denotes preferred causality.
For the example provided,
you would have the following , , and matrices:
The matrices of and are solved by determining the relationship of the state variables and their respective elements, as was described in the tetrahedron of state. The first step to solve the state equations is to list all of the governing equations for the bond graph. The table below shows the relationship between bonds and their governing equations.
"♦" denotes preferred causality.
For the example provided,
 the governing equations are the following.
#
#
#
#
#
#
#
#
#
#
#
These equations can be manipulated to yield the state equations. For this example, you are trying to find equations that relate and in terms of , , and .
To start you should recall from the tetrahedron of state that starting with equation 2, you can rearrange it so that . can be substituted for equation 4, while in equation 4, can be replaced by due to equation 3, which can then be replaced by equation 5. can likewise be replaced using equation 7, in which can be replaced with which can then be replaced with equation 10. Following these substituted yields the first state equation which is shown below.
The second state equation can likewise be solved, by recalling that . The second state equation is shown below.
Both equations can further be rearranged into matrix form. The result of which is below.
At this point the equations can be treated as any other
the governing equations are the following.
#
#
#
#
#
#
#
#
#
#
#
These equations can be manipulated to yield the state equations. For this example, you are trying to find equations that relate and in terms of , , and .
To start you should recall from the tetrahedron of state that starting with equation 2, you can rearrange it so that . can be substituted for equation 4, while in equation 4, can be replaced by due to equation 3, which can then be replaced by equation 5. can likewise be replaced using equation 7, in which can be replaced with which can then be replaced with equation 10. Following these substituted yields the first state equation which is shown below.
The second state equation can likewise be solved, by recalling that . The second state equation is shown below.
Both equations can further be rearranged into matrix form. The result of which is below.
At this point the equations can be treated as any other state-space representation
In control engineering, a state-space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations or difference equations. State variables are variables ...
problem.
International conferences on bond graph modeling (ECMS and ICBGM)
A bibliography on bond graph modeling may be extracted from the following conferences :ECMS-2013 27th European Conference on Modelling and Simulation, May 27–30, 2013, Ålesund, Norway
* [https://web.archive.org/web/20070125062943/http://www.scs.org/confernc/wmc/wmc07/icbgm07_FinalProgram_2.PDF ICBGM-2007: 8th International Conference on Bond Graph Modeling And Simulation, January 15–17, 2007, San Diego, California, U.S.A.]
ECMS-2006 20TH European Conference on Modelling and Simulation, May 28–31, 2006, Bonn, Germany
* ttp://gaia.csus.edu/~grandajj/icbgm05_FinalProgram.htm ICBGM-2005 International Conference on Bond Graph Modeling and Simulation, January 23–27, 2005, New Orleans, Louisiana, U.S.A.�
Papers
– ttps://web.archive.org/web/20080414235710/http://www.scs.org/search.cfm?presearch=db&dbrec=15 Papers
14TH European Simulation symposium October 23–26, 2002 Dresden, Germany
* ttp://gaia.csus.edu/~grandajj/WMC2001-ICBGM.htm ICBGM-2001 International Conference on Bond Graph Modeling and Simulation (ICBGM 2001), Phoenix, Arizona U.S.A.
European Simulation Multi-conference 23-26 May, 2000, Gent, Belgium
* [https://web.archive.org/web/20080408105504/http://www-control.eng.cam.ac.uk/extras/conferences/ICBGM99 ICBGM-1999 International Conference on Bond Graph Modeling and Simulation January 17–20, 1999 San Francisco, California]
ESS-97 9TH European Simulation Symposium and Exhibition Simulation in Industry, Passau, Germany, October 19–22, 1997
* ttp://www.scs-europe.net/conf/esm97/fintue.html 11th European Simulation Multiconference Istanbul, Turkey, June 1–4, 1997
ESM-1996 10th annual European Simulation Multiconference Budapest, Hungary, June 2–6, 1996
* ICBGM-1995 Int. Conf. on Bond Graph Modeling and Simulation (ICBGM’95), January 15–18, 1995,Las Vegas, Nevada.
See also
*20-sim
20-sim is commercial modeling and simulation program for multi-domain dynamic systems, which is developed by Controllab. With 20-sim, models can be entered as equations, block diagrams, bond graphs and physical components. 20-sim is widely used f ...
simulation software based on the bond graph theory
* AMESim
Simcenter Amesim is a commercial simulation software for the modeling and analysis of multi-domain systems. It is part of systems engineering domain and falls into the mechatronic engineering field.
The software package is a suite of tools used to ...
simulation software based on the bond graph theory
* Hybrid bond graph
* Coenergy
References
Further reading
* * * * * * * * * {{cite book , last=Borutzky , first=Wolfgang , date=2010 , title=Bond Graph Methodology , location=London , publisher=Springer , doi=10.1007/978-1-84882-882-7 , isbn=978-1-84882-881-0 * http://www.site.uottawa.ca/~rhabash/ESSModelFluid.pdf Explains modeling the bond graph in the fluid domain * http://www.dartmouth.edu/~sullivan/22files/Fluid_sys_anal_w_chart.pdf Explains modeling the bond graph in the fluid domainExternal links
Simscape
Official MATLAB/Simulink add-on library for graphical bond graph programming
Freeware MATLAB/Simulink add-on library for graphical bond graph programming Scientific visualization Diagrams Application-specific graphs Electrical engineering Mechanical engineering Modeling languages