Zipf's Law

Zipf's law (; ) is an empirical law stating that when a list of measured values is sorted in decreasing order, the value of the -th entry is often approximately inversely proportional to .

The best known instance of Zipf's law applies to the frequency table of words in a text or corpus of natural language:

$\ \mathsf\ \propto\ \frac ~.$

It is usually found that the most common word occurs approximately twice as often as the next common one, three times as often as the third most common, and so on. For example, in the Brown Corpus of American English text, the word "''the''" is the most frequently occurring word, and by itself accounts for nearly 7% of all word occurrences (69,971 out of slightly over 1 million). True to Zipf's law, the second-place word "''of''" accounts for slightly over 3.5% of words (36,411 occurrences), followed by "''and''" (28,852). It is often used in the following form, called Zipf-Mandelbrot law:

$\ \mathsf\ \propto\ \frac\$ where $\ a\$ and $\ b\$ are fitted parameters, with $\ a \approx 1$, and $\ b \approx 2.7 ~$.

This law is named after the American linguist George Kingsley Zipf, and is still an important concept in quantitative linguistics. It has been found to apply to many other types of data studied in the physical and social sciences.

In mathematical statistics, the concept has been formalized as the Zipfian distribution: A family of related discrete probability distributions whose rank-frequency distribution is an inverse power law relation. They are related to Benford's law and the Pareto distribution.

Some sets of time-dependent empirical data deviate somewhat from Zipf's law. Such empirical distributions are said to be quasi-Zipfian.

History

In 1913, the German physicist Felix Auerbach observed an inverse proportionality between the population sizes of cities, and their ranks when sorted by decreasing order of that variable.

Zipf's law had been discovered before Zipf, first by the French stenographer Jean-Baptiste Estoup in 1916, and also by G. Dewey in 1923, and by E. Condon in 1928.

The same relation for frequencies of words in natural language texts was observed by George Zipf in 1932, but he never claimed to have originated it. In fact, Zipf did not like mathematics. In his 1932 publication, the author speaks with disdain about mathematical involvement in linguistics, ''a.o. ibidem'', p. 21:
: ''... let me say here for the sake of any mathematician who may plan to formulate the ensuing data more exactly, the ability of the highly intense positive to become the highly intense negative, in my opinion, introduces the devil into the formula in the form of'' $\ \sqrt ~.$
The only mathematical expression Zipf used looks like which he "borrowed" from Alfred J. Lotka's 1926 publication.

The same relationship was found to occur in many other contexts, and for other variables besides frequency. For example, when corporations are ranked by decreasing size, their sizes are found to be inversely proportional to the rank. The same relation is found for personal incomes (where it is called Pareto principle), number of people watching the same TV channel, notes in music, cells transcriptomes, and more.

In 1992 bioinformatician Wentian Li published a short paper showing that Zipf's law emerges even in randomly generated texts. It included proof that the power law form of Zipf's law was a byproduct of ordering words by rank.

Formal definition

Formally, the Zipf distribution on elements assigns to the element of rank (counting from 1) the probability:

$\ f(k;N) ~=~ \begin \frac\ \frac\ , &\ \mbox\ 1 \le k \le N ~, \\ \\ ~~ 0 ~~ , &\ \mbox\ k < 1\ \mbox\ N < k ~. \end$ where is a normalization constant: The th harmonic number:

$H_N \equiv \sum_^N \frac ~.$

The distribution is sometimes generalized to an inverse power law with exponent instead of Namely,

$f(k;N,s) = \frac\,\frac$

where _, is a generalized harmonic number

$H_ = \sum_^N \frac ~.$

The generalized Zipf distribution can be extended to infinitely many items ( = ∞) only if the exponent exceeds In that case, the normalization constant _, becomes Riemann's zeta function,

$\zeta (s) = \sum_^\infty \frac < \infty ~.$

The infinite item case is characterized by the Zeta distribution and is called Lotka's law. If the exponent is or less, the normalization constant _, diverges as tends to infinity.

Empirical testing

Empirically, a data set can be tested to see whether Zipf's law applies by checking the goodness of fit of an empirical distribution to the hypothesized power law distribution with a Kolmogorov–Smirnov test, and then comparing the (log) likelihood ratio of the power law distribution to alternative distributions like an exponential distribution or lognormal distribution.

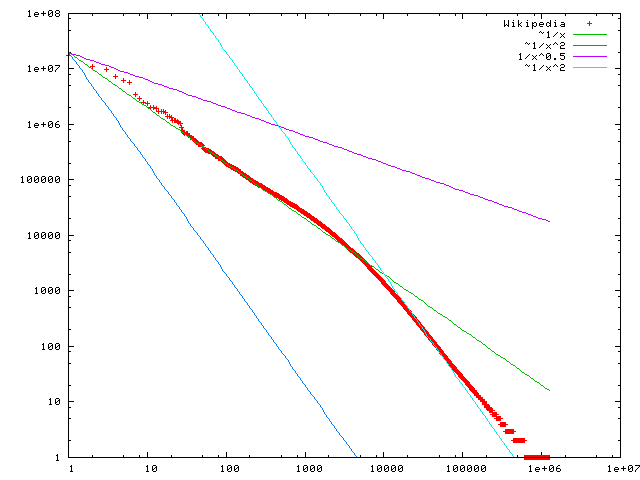
Zipf's law can be visualized by plotting the item frequency data on a log-log graph, with the axes being the logarithm of rank order, and logarithm of frequency. The data conform to Zipf's law with exponent to the extent that the plot approximates a linear (more precisely, affine) function with slope . For exponent one can also plot the reciprocal of the frequency (mean interword interval) against rank, or the reciprocal of rank against frequency, and compare the result with the line through the origin with slope

Statistical explanations

Although Zipf's Law holds for most natural languages, and even certain artificial ones such as Esperanto and Toki Pona, the reason is still not well understood. Recent reviews of generative processes for Zipf's law include Mitzenmacher, "A Brief History of Generative Models for Power Law and Lognormal Distributions", and Simkin, "Re-inventing Willis".

However, it may be partly explained by statistical analysis of randomly generated texts. Wentian Li has shown that in a document in which each character has been chosen randomly from a uniform distribution of all letters (plus a space character), the "words" with different lengths follow the macro-trend of Zipf's law (the more probable words are the shortest and have equal probability). In 1959, Vitold Belevitch observed that if any of a large class of well-behaved statistical distributions (not only the normal distribution) is expressed in terms of rank and expanded into a Taylor series, the first-order truncation of the series results in Zipf's law. Further, a second-order truncation of the Taylor series resulted in Mandelbrot's law.

The principle of least effort is another possible explanation:
Zipf himself proposed that neither speakers nor hearers using a given language wants to work any harder than necessary to reach understanding, and the process that results in approximately equal distribution of effort leads to the observed Zipf distribution.

A minimal explanation assumes that words are generated by monkeys typing randomly. If language is generated by a single monkey typing randomly, with fixed and nonzero probability of hitting each letter key or white space, then the words (letter strings separated by white spaces) produced by the monkey follows Zipf's law.

Another possible cause for the Zipf distribution is a preferential attachment process, in which the value of an item tends to grow at a rate proportional to (intuitively, "the rich get richer" or "success breeds success"). Such a growth process results in the Yule–Simon distribution, which has been shown to fit word frequency versus rank in language and population versus city rank better than Zipf's law. It was originally derived to explain population versus rank in species by Yule, and applied to cities by Simon.

A similar explanation is based on atlas models, systems of exchangeable positive-valued diffusion processes with drift and variance parameters that depend only on the rank of the process. It has been shown mathematically that Zipf's law holds for Atlas models that satisfy certain natural regularity conditions.

Related laws

A generalization of Zipf's law is the Zipf–Mandelbrot law, proposed by Benoit Mandelbrot, whose frequencies are:

$f(k;N,q,s) = \frac\ \frac ~.$

The constant is the Hurwitz zeta function evaluated at .

Zipfian distributions can be obtained from Pareto distributions by an exchange of variables.

The Zipf distribution is sometimes called the discrete Pareto distribution because it is analogous to the continuous Pareto distribution in the same way that the discrete uniform distribution is analogous to the continuous uniform distribution.

The tail frequencies of the Yule–Simon distribution are approximately

$f(k;\rho) \approx \frac$ for any choice of

In the parabolic fractal distribution, the logarithm of the frequency is a quadratic polynomial of the logarithm of the rank. This can markedly improve the fit over a simple power-law relationship. Like fractal dimension, it is possible to calculate Zipf dimension, which is a useful parameter in the analysis of texts.

It has been argued that Benford's law is a special bounded case of Zipf's law, with the connection between these two laws being explained by their both originating from scale invariant functional relations from statistical physics and critical phenomena. The ratios of probabilities in Benford's law are not constant. The leading digits of data satisfying Zipf's law with satisfy Benford's law.

Occurrences

City sizes

Following Auerbach's 1913 observation, there has been substantial examination of Zipf's law for city sizes. However, more recent empirical and theoretical studies have challenged the relevance of Zipf's law for cities.

Word frequencies in natural languages

In many texts in human languages, word frequencies approximately follow a Zipf distribution with exponent close to 1; that is, the most common word occurs about times the -th most common one.

The actual rank-frequency plot of a natural language text deviates in some extent from the ideal Zipf distribution, especially at the two ends of the range. The deviations may depend on the language, on the topic of the text, on the author, on whether the text was translated from another language, and on the spelling rules used. Some deviation is inevitable because of sampling error.

At the low-frequency end, where the rank approaches , the plot takes a staircase shape, because each word can occur only an integer number of times.

Zipf-euro-4 German, Russian, French, Italian, Medieval English.svg, German (1669), Russian (1972), French (1865), Italian (1840), and Medieval English (1460)
Zipf-semi-1 Arabic, Geez, Hebraic.svg, Ge'ez (14th century), Arabic (7th century), Hebrew (500–800), all with vowels
Zipf-asia-1 Chinese, Tibetan, Vietnamese.svg, Lhasa Tibetan, Chinese, Vietnamese, all with separated syllables
Zipf-heot-0 Hebrew - Books of the Torah.svg, First five books of the Old Testament (the Torah) in Hebrew, with vowels
Zipf-laot-0 Vulgate Pentateuch books.svg, First five books of the Old Testament (the Pentateuch) in the Latin Vulgate version
Zipf-lant-0 Vulgate Gospels.svg, First four books of the New Testament (the Gospels) in the Latin Vulgate version

In some Romance languages, the frequencies of the dozen or so most frequent words deviate significantly from the ideal Zipf distribution, because those words include articles inflected for grammatical gender and number.

In many East Asian languages, such as Chinese, Tibetan, and Vietnamese, each morpheme (word or word piece) consists of a single syllable; a word of English being often translated to a compound of two such syllables. The rank-frequency table for those morphemes deviates significantly from the ideal Zipf law, at both ends of the range.

Even in English, the deviations from the ideal Zipf's law become more apparent as one examines large collections of texts. Analysis of a corpus of 30,000 English texts showed that only about 15% of the texts in it have a good fit to Zipf's law. Slight changes in the definition of Zipf's law can increase this percentage up to close to 50%.

In these cases, the observed frequency-rank relation can be modeled more accurately as by separate Zipf–Mandelbrot laws distributions for different subsets or subtypes of words. This is the case for the frequency-rank plot of the first 10 million words of the English Wikipedia. In particular, the frequencies of the closed class of function words in English is better described with lower than 1, while open-ended vocabulary growth with document size and corpus size require greater than 1 for convergence of the Generalized Harmonic Series.

When a text is encrypted in such a way that every occurrence of each distinct plaintext word is always mapped to the same encrypted word (as in the case of simple substitution ciphers, like the Caesar ciphers, or simple codebook ciphers), the frequency-rank distribution is not affected. On the other hand, if separate occurrences of the same word may be mapped to two or more different words (as happens with the Vigenère cipher), the Zipf distribution will typically have a flat part at the high-frequency end.

Applications

Zipf's law has been used for extraction of parallel fragments of texts out of comparable corpora. Laurance Doyle and others have suggested the application of Zipf's law for detection of alien language in the search for extraterrestrial intelligence.

The frequency-rank word distribution is often characteristic of the author and changes little over time. This feature has been used in the analysis of texts for authorship attribution.

The word-like sign groups of the 15th-century codex Voynich Manuscript have been found to satisfy Zipf's law, suggesting that text is most likely not a hoax but rather written in an obscure language or cipher.

Whale Communication

Recent analysis of whale vocalization samples shows they contain recurring phonemes whose distribution appears to closely obey Zipf's Law. While this isn't proof that whale communication is a natural language, it is an intriguing discovery.

See also

*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
* Letter frequency
* Most common words in English

Notes

References

Further reading

*
*
*
*

External links

*—An article on Zipf's law applied to city populations
Seeing Around Corners (Artificial societies turn up Zipf's law)

* ttps://www.newscientist.com/article.ns?id=mg18524904.300 An analysis of income distributionbr>Zipf List of French words

Zipf list for English, French, Spanish, Italian, Swedish, Icelandic, Latin, Portuguese and Finnish from Gutenberg Project and online calculator to rank words in texts

Citations and the Zipf–Mandelbrot's lawZipf's Law examples and modelling (1985)Benford's law, Zipf's law, and the Pareto distribution
by Terence Tao.
*

{{Authority control

Discrete distributions
Computational linguistics
Power laws
Statistical laws
Empirical laws
Eponymous rules
Tails of probability distributions
Quantitative linguistics
Bibliometrics
Corpus linguistics
1949 introductions
Eponyms in mathematics