Zermelo's navigation problem on:
[Wikipedia]
[Google]
[Amazon]
In 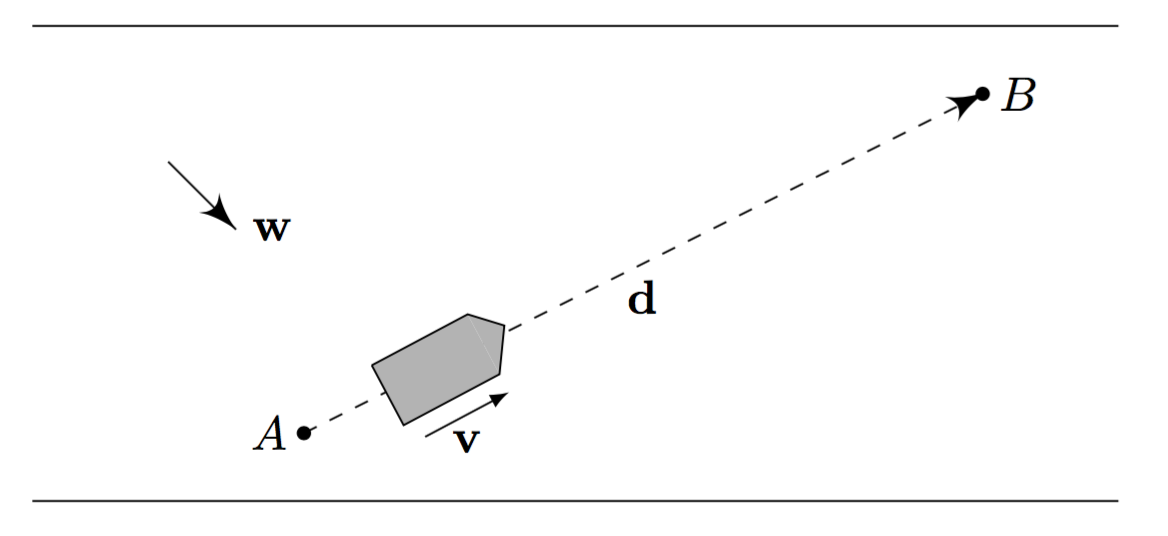 Without considering external forces such as current and wind, the optimal control is for the boat to always head towards . Its path then is a line segment from to , which is trivially optimal. With consideration of current and wind, if the combined force applied to the boat is non-zero the control for no current and wind does not yield the optimal path.
Without considering external forces such as current and wind, the optimal control is for the boat to always head towards . Its path then is a line segment from to , which is trivially optimal. With consideration of current and wind, if the combined force applied to the boat is non-zero the control for no current and wind does not yield the optimal path.
 This is an extension of the classical optimisation problem for
This is an extension of the classical optimisation problem for
mathematical optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfi ...
, Zermelo's navigation problem, proposed in 1931 by Ernst Zermelo
Ernst Friedrich Ferdinand Zermelo (, ; 27 July 187121 May 1953) was a German logician and mathematician, whose work has major implications for the foundations of mathematics. He is known for his role in developing Zermelo–Fraenkel axiomatic s ...
, is a classic optimal control problem that deals with a boat navigating on a body of water, originating from a point to a destination point . The boat is capable of a certain maximum speed, and the goal is to derive the best possible control to reach in the least possible time.
 Without considering external forces such as current and wind, the optimal control is for the boat to always head towards . Its path then is a line segment from to , which is trivially optimal. With consideration of current and wind, if the combined force applied to the boat is non-zero the control for no current and wind does not yield the optimal path.
Without considering external forces such as current and wind, the optimal control is for the boat to always head towards . Its path then is a line segment from to , which is trivially optimal. With consideration of current and wind, if the combined force applied to the boat is non-zero the control for no current and wind does not yield the optimal path.
History
In his 1931 article, Ernst Zermelo formulates the following problem: This is an extension of the classical optimisation problem for
This is an extension of the classical optimisation problem for geodesics
In geometry, a geodesic () is a curve representing in some sense the shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. ...
–
minimising the length of a curve
connecting points and , with the added complexity of considering some wind velocity. Although it is usually impossible to find an exact solution in most cases, the general case was solved by Zermelo himself in the form of a partial differential equation, known as Zermelo's equation, which can be numerically solved.
The problem of navigating an airship which is surrounded by air, was presented first in 1929 at a conference by Ernst Zermelo. Other mathematicians have answered the challenge over the following years. The dominant technique for solving the equations is the calculus of variations
The calculus of variations (or Variational Calculus) is a field of mathematical analysis that uses variations, which are small changes in functions
and functionals, to find maxima and minima of functionals: mappings from a set of functions t ...
.
Constant-wind case
The case of constant wind is easy to solve exactly. Let , and suppose that to minimise the travel time the ship travels at a constant maximum speed . Thus the position of the ship at time is . Let be the time of arrival at , so that . Taking thedot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a scalar as a result". It is also used sometimes for other symmetric bilinear forms, for example in a pseudo-Euclidean space. is an alg ...
of this with and respectively results in
and . Eliminating and writing this system as a quadratic in results in . Upon solving this, taking the positive square-root since is positive, we obtain
:
Claim: This defines a metric on , provided .
Proof
By our assumption, clearly with equality if and only if . Trivially if , we have