Widlar current mirror on:
[Wikipedia]
[Google]
[Amazon]
 ]
A Widlar current source is a modification of the basic two-
]
A Widlar current source is a modification of the basic two-
''IC voltage regulators''
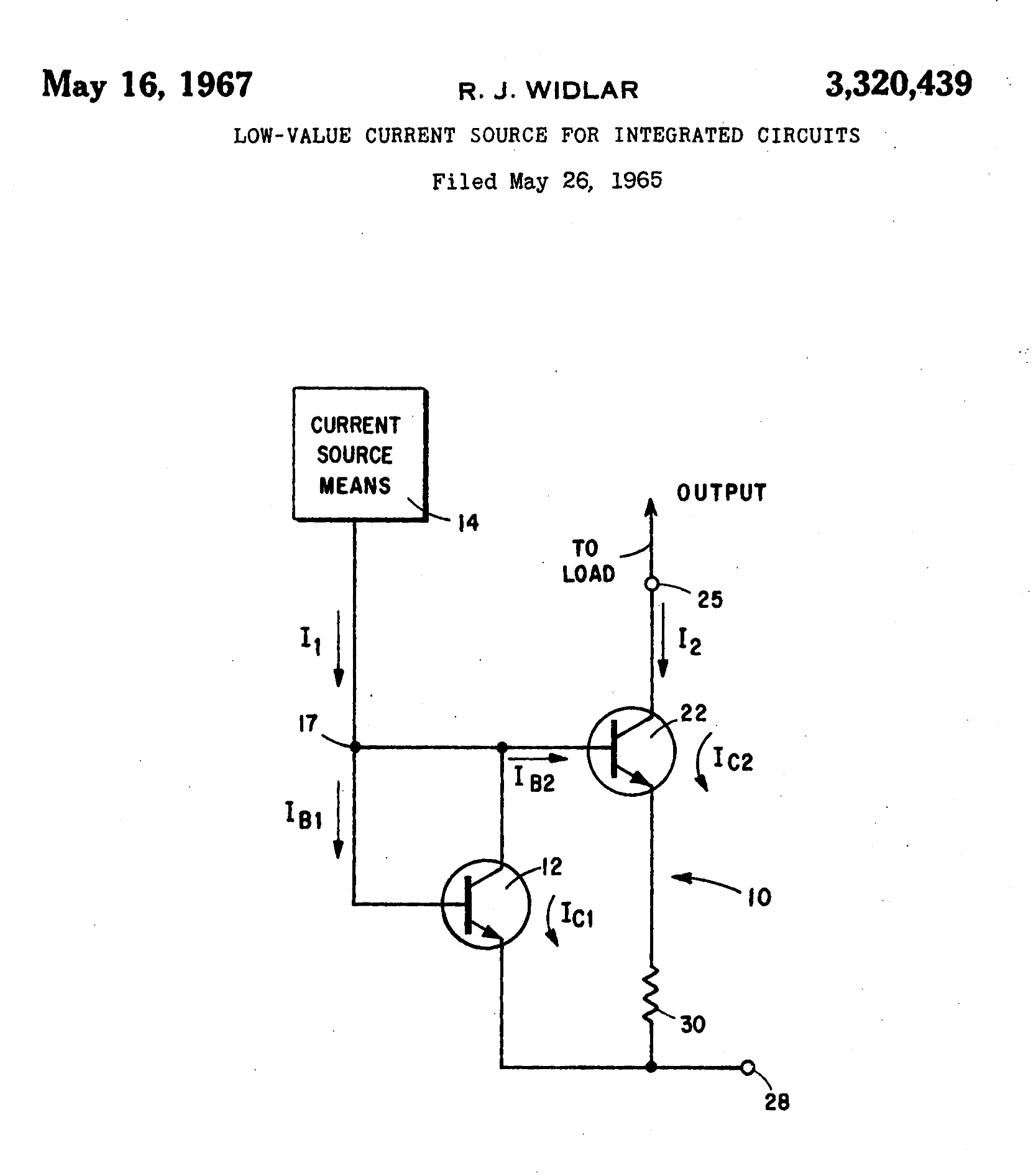
This circuit is named after its inventor,
Low-value current source for integrated circuits''
/ref>See Widlar
''Some circuit design techniques for linear integrated circuits''
an
''Design techniques for monolithic operational amplifiers''
/ref>
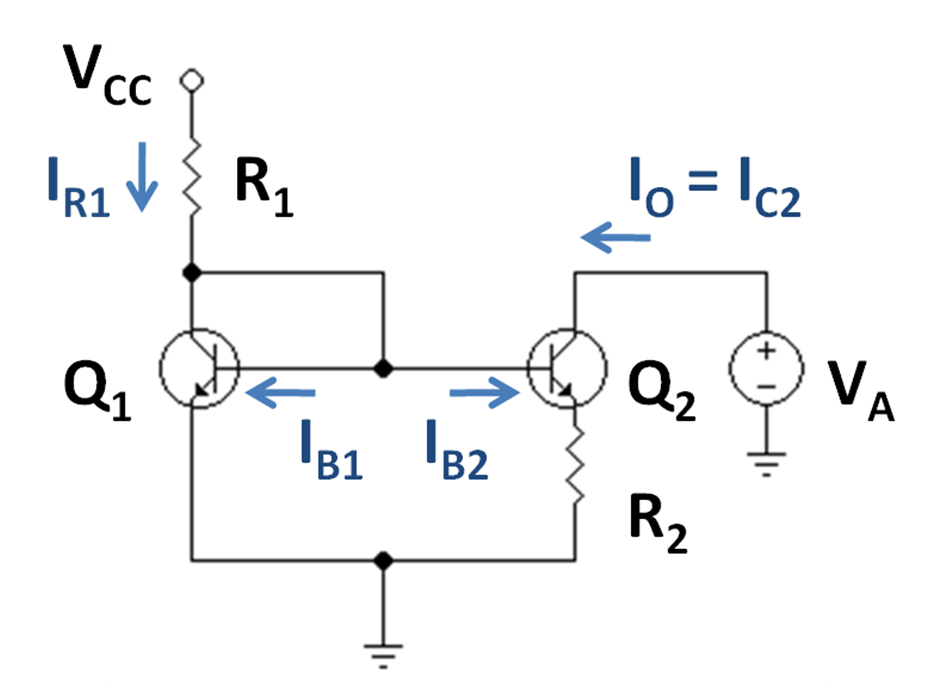 Figure 1 is an example Widlar current source using bipolar transistors, where the emitter resistor R2 is connected to the output transistor Q2, and has the effect of reducing the current in Q2 relative to Q1. The key to this circuit is that the voltage drop across the resistor ''R''2 subtracts from the base-emitter voltage of transistor ''Q''2, thereby turning this transistor off compared to transistor ''Q''1. This observation is expressed by equating the base voltage expressions found on either side of the circuit in Figure 1 as:
:
where β2 is the beta-value of the output transistor, which is not the same as that of the input transistor, in part because the currents in the two transistors are very different. The variable ''I''B2 is the base current of the output transistor, ''V''BE refers to base-emitter voltage. This equation implies (using the
Figure 1 is an example Widlar current source using bipolar transistors, where the emitter resistor R2 is connected to the output transistor Q2, and has the effect of reducing the current in Q2 relative to Q1. The key to this circuit is that the voltage drop across the resistor ''R''2 subtracts from the base-emitter voltage of transistor ''Q''2, thereby turning this transistor off compared to transistor ''Q''1. This observation is expressed by equating the base voltage expressions found on either side of the circuit in Figure 1 as:
:
where β2 is the beta-value of the output transistor, which is not the same as that of the input transistor, in part because the currents in the two transistors are very different. The variable ''I''B2 is the base current of the output transistor, ''V''BE refers to base-emitter voltage. This equation implies (using the
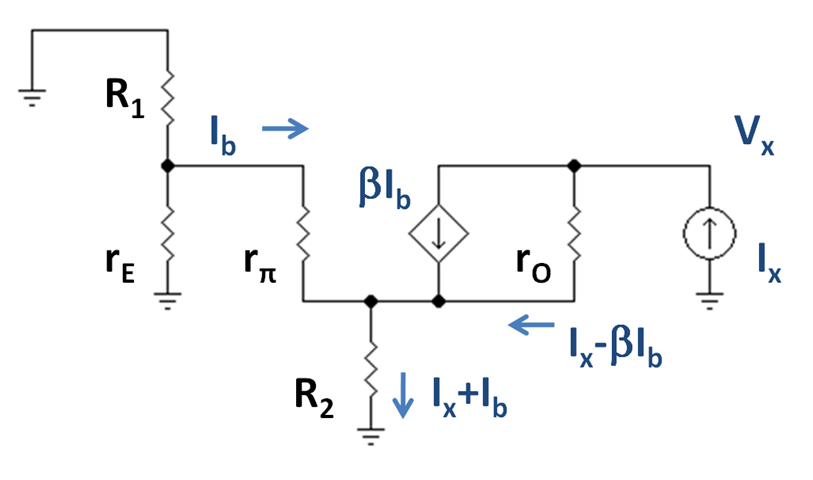 An important property of a current source is its small signal incremental output impedance, which should ideally be infinite. The Widlar circuit introduces local current feedback for transistor . Any increase in the current in ''Q''2 increases the voltage drop across ''R''2, reducing the ''V''BE for ''Q''2, thereby countering the increase in current. This feedback means the output impedance of the circuit is increased, because the feedback involving ''R''2 forces use of a larger voltage to drive a given current.
Output resistance is found using a small-signal model for the circuit, shown in Figure 2. Transistor ''Q''1 is replaced by its small-signal emitter resistance ''r''E because it is diode connected.In a ''diode-connected transistor'' the collector is short-circuited to the base, so the transistor collector-base junction has no time-varying voltage across it. As a result, the transistor behaves like the base-emitter diode, which at low frequencies has a small-signal circuit that is simply the resistor ''r''E = ''V''T / ''I''E, with ''I''E the DC
An important property of a current source is its small signal incremental output impedance, which should ideally be infinite. The Widlar circuit introduces local current feedback for transistor . Any increase in the current in ''Q''2 increases the voltage drop across ''R''2, reducing the ''V''BE for ''Q''2, thereby countering the increase in current. This feedback means the output impedance of the circuit is increased, because the feedback involving ''R''2 forces use of a larger voltage to drive a given current.
Output resistance is found using a small-signal model for the circuit, shown in Figure 2. Transistor ''Q''1 is replaced by its small-signal emitter resistance ''r''E because it is diode connected.In a ''diode-connected transistor'' the collector is short-circuited to the base, so the transistor collector-base junction has no time-varying voltage across it. As a result, the transistor behaves like the base-emitter diode, which at low frequencies has a small-signal circuit that is simply the resistor ''r''E = ''V''T / ''I''E, with ''I''E the DC
 The current dependence of the resistances ''r''π and ''r''O is discussed in the article
The current dependence of the resistances ''r''π and ''r''O is discussed in the article
Current mirrors and active loads: Mu-Huo Cheng
Analog circuits Electronic design de:Stromspiegel#Beispiele
transistor
upright=1.4, gate (G), body (B), source (S) and drain (D) terminals. The gate is separated from the body by an insulating layer (pink).
A transistor is a semiconductor device used to Electronic amplifier, amplify or electronic switch, switch ...
current mirror
A current mirror is a circuit designed to copy a current through one active device by controlling the current in another active device of a circuit, keeping the output current constant regardless of loading. The current being "copied" can be, and ...
that incorporates an emitter degeneration resistor for only the output transistor, enabling the current source to generate low currents using only moderate resistor values.
The Widlar circuit may be used with bipolar transistor
A bipolar junction transistor (BJT) is a type of transistor that uses both electrons and electron holes as charge carriers. In contrast, a unipolar transistor, such as a field-effect transistor, uses only one kind of charge carrier. A bipolar t ...
s, MOS transistors, and even vacuum tube
A vacuum tube, electron tube, valve (British usage), or tube (North America), is a device that controls electric current flow in a high vacuum between electrodes to which an electric potential difference has been applied.
The type known as ...
s. An example application is the 741 operational amplifier, and Widlar used the circuit as a part in many designs.See, for example, Figure 2 i''IC voltage regulators''
This circuit is named after its inventor,
Bob Widlar
Robert John Widlar (pronounced ''wide-lar''; November 30, 1937 – February 27, 1991) was an American electronics engineer and a designer of linear integrated circuits (ICs).
Early years
Widlar was born November 30, 1937 in Cleveland to par ...
, and was patented in 1967.RJ Widlar: US Patent Number 03320439; Filed May 26, 1965; Granted May 16, 1967:Low-value current source for integrated circuits''
/ref>See Widlar
''Some circuit design techniques for linear integrated circuits''
an
''Design techniques for monolithic operational amplifiers''
/ref>
DC analysis
Shockley diode equation
The ''Shockley diode equation'' or the ''diode law'', named after transistor co-inventor William Shockley of Bell Telephone Laboratories, gives the I–V (current-voltage) characteristic of an idealized diode in either forward or reverse bias (appl ...
):
''Eq. 1''
:
where ''V''T is the thermal voltage.
This equation makes the approximation that the currents are both much larger than the scale currents, ''I''S1 and ''I''S2; an approximation valid except for current levels near cut off. In the following, the scale currents are assumed to be identical; in practice, this needs to be specifically arranged.
Design procedure with specified currents
To design the mirror, the output current must be related to the two resistor values ''R''1 and ''R''2. A basic observation is that the output transistor is in active mode only so long as its collector-base voltage is non-zero. Thus, the simplest bias condition for design of the mirror sets the applied voltage ''V''A to equal the base voltage ''V''B. This minimum useful value of ''V''A is called the '' compliance voltage'' of the current source. With that bias condition, the Early effect plays no role in the design.Of course, one might imagine a design where the output resistance of the mirror is a major consideration. Then a different approach is necessary. These considerations suggest the following design procedure: * Select the desired output current, ''I''O = ''I''C2. * Select the reference current, ''I''R1, assumed to be larger than the output current, probably considerably larger (that is the purpose of the circuit). * Determine the input collector current of ''Q''1, ''I''C1: :: * Determine the base voltage ''V''BE1 using the Shockley diode law :: :where ''I''S is a device parameter sometimes called the ''scale current''. :The value of base voltage also sets the compliance voltage ''V''A = ''V''BE1. This voltage is the lowest voltage for which the mirror works properly. * Determine ''R''1: :: * Determine the emitter leg resistance ''R''2 using '' Eq. 1'' (to reduce clutter, the scale currents are chosen equal): ::Finding the current with given resistor values
The inverse of the design problem is finding the current when the resistor values are known. An iterative method is described next. Assume the current source is biased so the collector-base voltage of the output transistor ''Q''2 is zero. The current through ''R''1 is the input or reference current given as, : Rearranging, ''I''C1 is found as: ''Eq. 2'' : The diode equation provides: ''Eq. 3'' : '' Eq.1'' provides: : These three relations are a nonlinear, implicit determination for the currents that can be solved by iteration. * We guess starting values for ''I''C1 and ''I''C2. * We find a value for ''V''BE1: *: * We find a new value for ''I''C1: *: * We find a new value for ''I''C2: *: This procedure is repeated to convergence, and is set up conveniently in a spreadsheet. One simply uses a macro to copy the new values into the spreadsheet cells holding the initial values to obtain the solution in short order. Note that with the circuit as shown, if VCC changes, the output current will change. Hence, to keep the output current constant despite fluctuations in ''V''CC, the circuit should be driven by aconstant current source
A current source is an electronic circuit that delivers or absorbs an electric current which is independent of the voltage across it.
A current source is the dual of a voltage source. The term ''current sink'' is sometimes used for sources f ...
rather than using the resistor ''R''1.
Exact solution
Thetranscendental equation
In applied mathematics, a transcendental equation is an equation over the real (or complex) numbers that is not algebraic, that is, if at least one of its sides describes a transcendental function.
Examples include:
:\begin
x &= e^ \\
x &= ...
s above can be solved exactly in terms of the Lambert W function
In mathematics, the Lambert function, also called the omega function or product logarithm, is a multivalued function, namely the branches of the converse relation of the function , where is any complex number and is the exponential function ...
.
Output impedance
Q-point
In electronics, biasing is the setting of DC (direct current) operating conditions (current and voltage) of an active device in an amplifier. Many electronic devices, such as diodes, transistors and vacuum tubes, whose function is processin ...
emitter current. See diode small-signal circuit. Transistor ''Q''2 is replaced with its hybrid-pi model The hybrid-pi model is a popular circuit model used for analyzing the small signal behavior of bipolar junction and field effect transistors. Sometimes it is also called Giacoletto model because it was introduced by L.J. Giacoletto in 1969. The ...
. A test current ''I''x is attached at the output.
Using the figure, the output resistance is determined using Kirchhoff's laws. Using Kirchhoff's voltage law from the ground on the left to the ground connection of ''R''2:
:
Rearranging:
:
Using Kirchhoff's voltage law from the ground connection of ''R''2 to the ground of the test current:
:
or, substituting for ''I''b:
''Eq. 4''
:
According to '' Eq. 4'', the output resistance of the Widlar current source is increased over that of the output transistor itself (which is ''r''O) so long as ''R''2 is large enough compared to the ''r''π of the output transistor (large resistances ''R''2 make the factor multiplying ''r''O approach the value (β + 1)). The output transistor carries a low current, making ''r''π large, and increase in ''R''2 tends to reduce this current further, causing a correlated increase in ''r''π. Therefore, a goal of ''R''2 ≫ ''r''π can be unrealistic, and further discussion is provided below. The resistance ''R''1∥''r''E usually is small because the emitter resistance ''r''E usually is only a few ohms.
Current dependence of output resistance
hybrid-pi model The hybrid-pi model is a popular circuit model used for analyzing the small signal behavior of bipolar junction and field effect transistors. Sometimes it is also called Giacoletto model because it was introduced by L.J. Giacoletto in 1969. The ...
. The current dependence of the resistor values is:
:
and
:
is the output resistance due to the Early effect when ''V''CB = 0 V (device parameter ''V''A is the Early voltage).
From earlier in this article (setting the scale currents equal for convenience):
''Eq. 5''
:
Consequently, for the usual case of small ''r''E, and neglecting the second term in ''R''O with the expectation that the leading term involving ''r''O is much larger:
''Eq. 6''
:
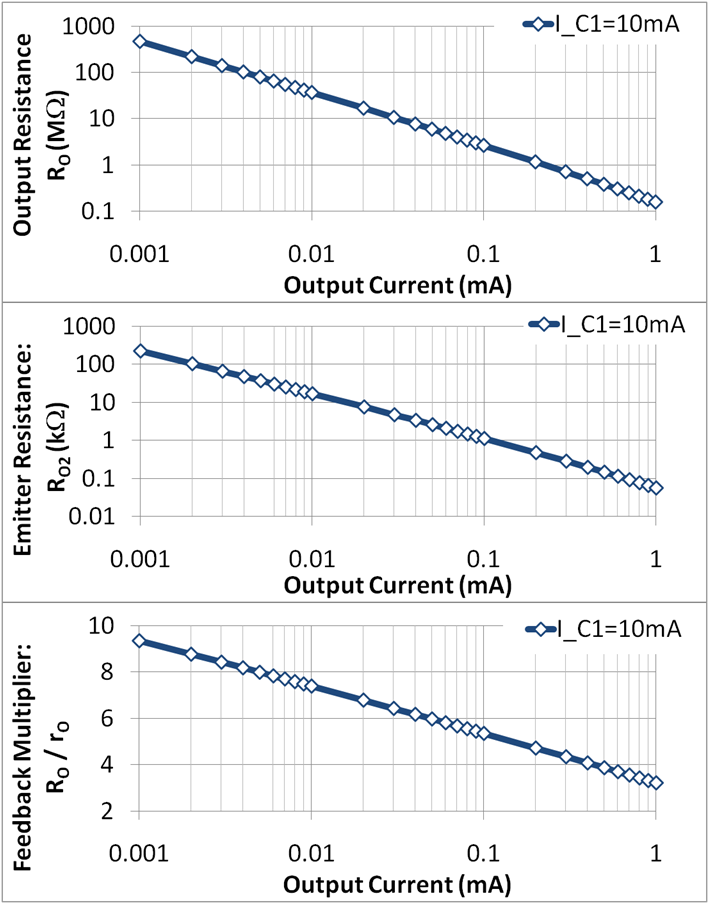
where the last form is found by substituting '' Eq. 5'' for ''R''2. '' Eq. 6'' shows that a value of output resistance much larger than ''r''O of the output transistor results only for designs with ''I''C1 >> ''I''C2. Figure 3 shows that the circuit output resistance ''R''O is not determined so much by feedback as by the current dependence of the resistance ''r''O of the output transistor (the output resistance in Figure 3 varies four orders of magnitude, while the feedback factor varies only by one order of magnitude).
Increase of ''I''C1 to increase the feedback factor also results in increased compliance voltage, not a good thing as that means the current source operates over a more restricted voltage range. So, for example, with a goal for compliance voltage set, placing an upper limit upon ''I''C1, and with a goal for output resistance to be met, the maximum value of output current ''I''C2 is limited.
The center panel in Figure 3 shows the design trade-off between emitter leg resistance and the output current: a lower output current requires a larger leg resistor, and hence a larger area for the design. An upper bound on area therefore sets a lower bound on the output current and an upper bound on the circuit output resistance.
'' Eq. 6'' for ''R''O depends upon selecting a value of ''R''2 according to '' Eq. 5''. That means '' Eq. 6'' is not a ''circuit behavior'' formula, but a ''design value'' equation. Once ''R''2 is selected for a particular design objective using '' Eq. 5'', thereafter its value is fixed. If circuit operation causes currents, voltages or temperatures to deviate from the designed-for values; then to predict changes in ''R''O caused by such deviations, '' Eq. 4'' should be used, not '' Eq. 6''.
See also
*Current source
A current source is an electronic circuit that delivers or absorbs an electric current which is independent of the voltage across it.
A current source is the dual of a voltage source. The term ''current sink'' is sometimes used for sources fed ...
* Current mirror
A current mirror is a circuit designed to copy a current through one active device by controlling the current in another active device of a circuit, keeping the output current constant regardless of loading. The current being "copied" can be, and ...
* Wilson current source
References
Further reading
* * {{cite book , title=Microelectronics: Analysis and Design , author=Sundaram Natarajan , page=319 , url=https://books.google.com/books?id=92LWHJjKcvgC&q=+%22Widlar+current+source%22&pg=PA320 , isbn=0-07-059096-6 , publisher=Tata McGraw-Hill , year=2005Current mirrors and active loads: Mu-Huo Cheng
Analog circuits Electronic design de:Stromspiegel#Beispiele