White-noise

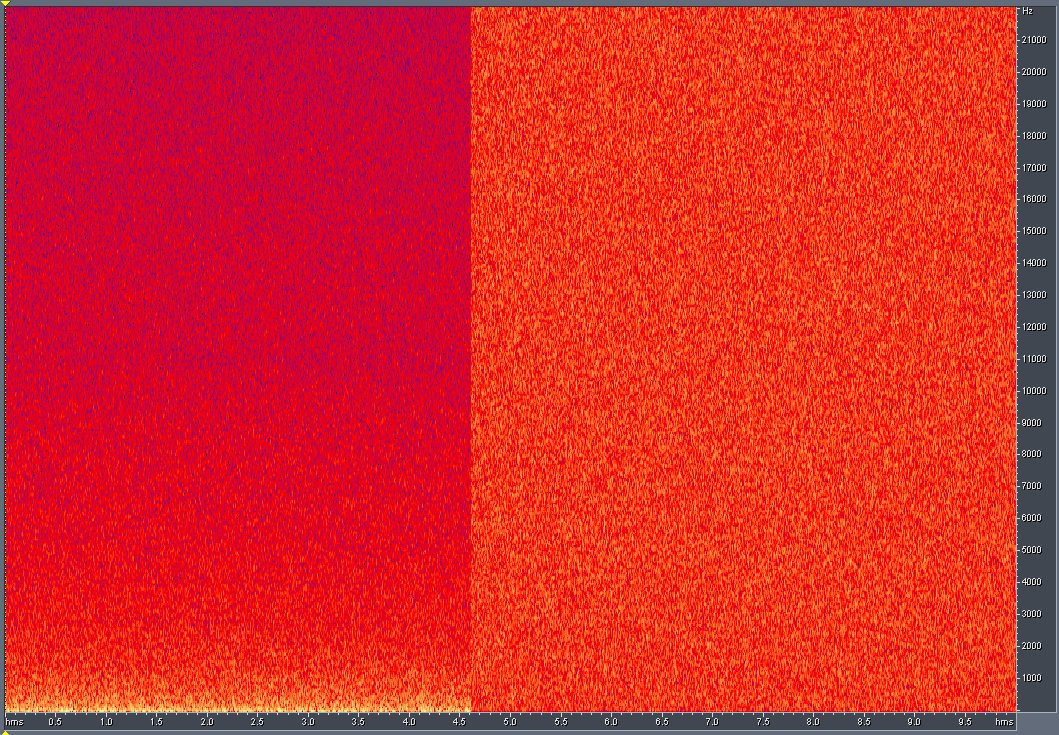
In signal processing, white noise is a random signal having equal intensity at different frequencies, giving it a constant power spectral density. The term is used, with this or similar meanings, in many scientific and technical disciplines, including physics, acoustical engineering, telecommunications, and statistical forecasting. White noise refers to a statistical model for signals and signal sources, rather than to any specific signal. White noise draws its name from white light, although light that appears white generally does not have a flat power spectral density over the visible band.

In discrete time, white noise is a discrete signal whose samples are regarded as a sequence of serially uncorrelated random variables with zero mean and finite variance; a single realization of white noise is a random shock. Depending on the context, one may also require that the samples be independent and have identical probability distribution (in other words independent and identically distributed random variables are the simplest representation of white noise). In particular, if each sample has a normal distribution with zero mean, the signal is said to be additive white Gaussian noise.

The samples of a white noise signal may be sequential in time, or arranged along one or more spatial dimensions. In digital image processing, the pixels of a ''white noise image'' are typically arranged in a rectangular grid, and are assumed to be independent random variables with uniform probability distribution over some interval. The concept can be defined also for signals spread over more complicated domains, such as a sphere or a torus.

An ''infinite-bandwidth white noise signal'' is a purely theoretical construction. The bandwidth of white noise is limited in practice by the mechanism of noise generation, by the transmission medium and by finite observation capabilities. Thus, random signals are considered "white noise" if they are observed to have a flat spectrum over the range of frequencies that are relevant to the context. For an audio signal, the relevant range is the band of audible sound frequencies (between 20 and 20,000 Hz). Such a signal is heard by the human ear as a ''hissing sound'', resembling the /h/ sound in a sustained aspiration. On the other hand, the "sh" sound in "ash" is a colored noise because it has a formant structure. In music and acoustics, the term "white noise" may be used for any signal that has a similar hissing sound.

The term white noise is sometimes used in the context of phylogenetically based statistical methods to refer to a lack of phylogenetic pattern in comparative data. It is sometimes used analogously in nontechnical contexts to mean "random talk without meaningful contents".
Claire Shipman (2005), ''Good Morning America'': "The political rhetoric on Social Security is white noise." Said on ABC's ''Good Morning America'' TV show, January 11, 2005.

Statistical properties

Any distribution of values is possible (although it must have zero DC component). Even a binary signal which can only take on the values 1 or 0 will be white if the sequence is statistically uncorrelated. Noise having a continuous distribution, such as a normal distribution, can of course be white.

It is often incorrectly assumed that Gaussian noise (i.e., noise with a Gaussian amplitude distributionsee normal distribution) necessarily refers to white noise, yet neither property implies the other. Gaussianity refers to the probability distribution with respect to the value, in this context the probability of the signal falling within any particular range of amplitudes, while the term 'white' refers to the way the signal power is distributed (i.e., independently) over time or among frequencies.

White noise is the generalized mean-square derivative of the Wiener process or Brownian motion.

A generalization to random elements on infinite dimensional spaces, such as random fields, is the white noise measure.

Practical applications

Music

White noise is commonly used in the production of electronic music, usually either directly or as an input for a filter to create other types of noise signal. It is used extensively in audio synthesis, typically to recreate percussive instruments such as cymbals or snare drums which have high noise content in their frequency domain. A simple example of white noise is a nonexistent radio station (static).

Electronics engineering

White noise is also used to obtain the impulse response of an electrical circuit, in particular of amplifiers and other audio equipment. It is not used for testing loudspeakers as its spectrum contains too great an amount of high-frequency content. Pink noise, which differs from white noise in that it has equal energy in each octave, is used for testing transducers such as loudspeakers and microphones.

Computing

White noise is used as the basis of some random number generators. For example, Random.org uses a system of atmospheric antennae to generate random digit patterns from white noise.

Tinnitus treatment

White noise is a common synthetic noise source used for sound masking by a tinnitus masker. White noise machines and other white noise sources are sold as privacy enhancers and sleep aids (see music and sleep) and to mask tinnitus. The Marpac Sleep-Mate was the first domestic use white noise machine built in 1962 by traveling salesman Jim Buckwalter. Alternatively, the use of an FM radio tuned to unused frequencies ("static") is a simpler and more cost-effective source of white noise. However, white noise generated from a common commercial radio receiver tuned to an unused frequency is extremely vulnerable to being contaminated with spurious signals, such as adjacent radio stations, harmonics from non-adjacent radio stations, electrical equipment in the vicinity of the receiving antenna causing interference, or even atmospheric events such as solar flares and especially lightning.

There is evidence that white noise exposure therapies may induce maladaptive changes in the brain that degrade neurological health and compromise cognition.

Work environment

The effects of white noise upon cognitive function are mixed. Recently, a small study found that white noise background stimulation improves cognitive functioning among secondary students with attention deficit hyperactivity disorder (ADHD), while decreasing performance of non-ADHD students. Other work indicates it is effective in improving the mood and performance of workers by masking background office noise, but decreases cognitive performance in complex card sorting tasks.

Similarly, an experiment was carried out on sixty-six healthy participants to observe the benefits of using white noise in a learning environment. The experiment involved the participants identifying different images whilst having different sounds in the background. Overall the experiment showed that white noise does in fact have benefits in relation to learning. The experiments showed that white noise improved the participants' learning abilities and their recognition memory slightly.

Mathematical definitions

White noise vector

A random vector (that is, a partially indeterminate process that produces vectors of real numbers) is said to be a white noise vector or white random vector if its components each have a probability distribution with zero mean and finite variance, and are statistically independent: that is, their joint probability distribution must be the product of the distributions of the individual components.
Jeffrey A. Fessler (1998),
On Transformations of Random Vectors.
' Technical report 314, Dept. of Electrical Engineering and Computer Science, Univ. of Michigan. (PDF)

A necessary (but, in general, not sufficient) condition for statistical independence of two variables is that they be statistically uncorrelated; that is, their covariance is zero. Therefore, the covariance matrix ''R'' of the components of a white noise vector ''w'' with ''n'' elements must be an ''n'' by ''n'' diagonal matrix, where each diagonal element ''R_ii'' is the variance of component ''w_i''; and the correlation matrix must be the ''n'' by ''n'' identity matrix.

If, in addition to being independent, every variable in ''w'' also has a normal distribution with zero mean and the same variance $\sigma^2$, ''w'' is said to be a Gaussian white noise vector. In that case, the joint distribution of ''w'' is a multivariate normal distribution; the independence between the variables then implies that the distribution has spherical symmetry in ''n''-dimensional space. Therefore, any orthogonal transformation of the vector will result in a Gaussian white random vector. In particular, under most types of discrete Fourier transform, such as FFT and Hartley, the transform ''W'' of ''w'' will be a Gaussian white noise vector, too; that is, the ''n'' Fourier coefficients of ''w'' will be independent Gaussian variables with zero mean and the same variance $\sigma^2$.

The power spectrum ''P'' of a random vector ''w'' can be defined as the expected value of the squared modulus of each coefficient of its Fourier transform ''W'', that is, ''P_i'' = E(, ''W_i'', ²). Under that definition, a Gaussian white noise vector will have a perfectly flat power spectrum, with ''P_i'' = ''σ''² for all ''i''.

If ''w'' is a white random vector, but not a Gaussian one, its Fourier coefficients ''W_i'' will not be completely independent of each other; although for large ''n'' and common probability distributions the dependencies are very subtle, and their pairwise correlations can be assumed to be zero.

Often the weaker condition "statistically uncorrelated" is used in the definition of white noise, instead of "statistically independent". However, some of the commonly expected properties of white noise (such as flat power spectrum) may not hold for this weaker version. Under this assumption, the stricter version can be referred to explicitly as independent white noise vector.Eric Zivot and Jiahui Wang (2006)
Modeling Financial Time Series with S-PLUS
Second Edition. (PDF) Other authors use strongly white and weakly white instead.Francis X. Diebold (2007),
Elements of Forecasting
'' 4th edition. (PDF)

An example of a random vector that is "Gaussian white noise" in the weak but not in the strong sense is x= _1,x_2/math> where $x_1$ is a normal random variable with zero mean, and $x_2$ is equal to $+x_1$ or to $-x_1$, with equal probability. These two variables are uncorrelated and individually normally distributed, but they are not jointly normally distributed and are not independent. If $x$ is rotated by 45 degrees, its two components will still be uncorrelated, but their distribution will no longer be normal.

In some situations one may relax the definition by allowing each component of a white random vector $w$ to have non-zero expected value $\mu$. In image processing especially, where samples are typically restricted to positive values, one often takes $\mu$ to be one half of the maximum sample value. In that case, the Fourier coefficient $W_0$ corresponding to the zero-frequency component (essentially, the average of the $w_i$) will also have a non-zero expected value $\mu\sqrt$; and the power spectrum $P$ will be flat only over the non-zero frequencies.

Discrete-time white noise

A discrete-time stochastic process $W(n)$ is a generalization of random vectors with a finite number of components to infinitely many components. A discrete-time stochastic process $W(n)$ is called white noise if its mean does not depend on the time $n$ and is equal to zero, i.e. $\operatorname$(n)= 0 and if the autocorrelation function $R_(n) = \operatorname$(k+n)W(k)/math> has a nonzero value only for $n = 0$, i.e. $R_(n) = \sigma^2 \delta(n)$.

Continuous-time white noise

In order to define the notion of "white noise" in the theory of continuous-time signals, one must replace the concept of a "random vector" by a continuous-time random signal; that is, a random process that generates a function $w$ of a real-valued parameter $t$.

Such a process is said to be white noise in the strongest sense if the value $w(t)$ for any time $t$ is a random variable that is statistically independent of its entire history before $t$. A weaker definition requires independence only between the values $w(t_1)$ and $w(t_2)$ at every pair of distinct times $t_1$ and $t_2$. An even weaker definition requires only that such pairs $w(t_1)$ and $w(t_2)$ be uncorrelated.

''White noise process''
By Econterms via About.com. Accessed on 2013-02-12.
As in the discrete case, some authors adopt the weaker definition for "white noise", and use the qualifier independent to refer to either of the stronger definitions. Others use weakly white and strongly white to distinguish between them.

However, a precise definition of these concepts is not trivial, because some quantities that are finite sums in the finite discrete case must be replaced by integrals that may not converge. Indeed, the set of all possible instances of a signal $w$ is no longer a finite-dimensional space $\mathbb^n$, but an infinite-dimensional function space. Moreover, by any definition a white noise signal $w$ would have to be essentially discontinuous at every point; therefore even the simplest operations on $w$, like integration over a finite interval, require advanced mathematical machinery.

Some authors require each value $w(t)$ to be a real-valued random variable with expectation $\mu$ and some finite variance $\sigma^2$. Then the covariance $\mathrm(w(t_1)\cdot w(t_2))$ between the values at two times $t_1$ and $t_2$ is well-defined: it is zero if the times are distinct, and $\sigma^2$ if they are equal. However, by this definition, the integral
: $W_ = \int_a^ w(t)\, dt$
over any interval with positive width $r$ would be simply the width times the expectation: $r\mu$. This property would render the concept inadequate as a model of physical "white noise" signals.

Therefore, most authors define the signal $w$ indirectly by specifying non-zero values for the integrals of $w(t)$ and $, w(t), ^2$ over any interval ,a+r/math>, as a function of its width $r$. In this approach, however, the value of $w(t)$ at an isolated time cannot be defined as a real-valued random variable. Also the covariance $\mathrm(w(t_1)\cdot w(t_2))$ becomes infinite when $t_1=t_2$; and the autocorrelation function $\mathrm(t_1,t_2)$ must be defined as $N \delta(t_1-t_2)$, where $N$ is some real constant and $\delta$ is Dirac's "function".

In this approach, one usually specifies that the integral $W_I$ of $w(t)$ over an interval I= ,b/math> is a real random variable with normal distribution, zero mean, and variance $(b-a)\sigma^2$; and also that the covariance $\mathrm(W_I\cdot W_J)$ of the integrals $W_I$, $W_J$ is $r\sigma^2$, where $r$ is the width of the intersection $I\cap J$ of the two intervals $I,J$. This model is called a Gaussian white noise signal (or process).

In the mathematical field known as white noise analysis, a Gaussian white noise $w$ is defined as a stochastic tempered distribution, i.e. a random variable with values in the space $\mathcal S'(\mathbb R)$ of tempered distributions. Analogous to the case for finite-dimensional random vectors, a probability law on the infinite-dimensional space $\mathcal S'(\mathbb R)$ can be defined via its characteristic function (existence and uniqueness are guaranteed by an extension of the Bochner–Minlos theorem, which goes under the name Bochner–Minlos–Sazanov theorem); analogously to the case of the multivariate normal distribution $X \sim \mathcal N_n (\mu , \Sigma )$, which has characteristic function
: $\forall k \in \mathbb R^n: \quad \mathrm(\mathrm e^) = \mathrm e^ ,$
the white noise $w : \Omega \to \mathcal S'(\mathbb R)$ must satisfy
: $\forall \varphi \in \mathcal S (\mathbb R) : \quad \mathrm(\mathrm e^) = \mathrm e^,$
where $\langle w, \varphi \rangle$ is the natural pairing of the tempered distribution $w(\omega)$ with the Schwartz function $\varphi$, taken scenariowise for $\omega \in \Omega$, and $\, \varphi \, _2^2 = \int_ \vert \varphi (x) \vert^2\,\mathrm d x$.

Mathematical applications

Time series analysis and regression

In statistics and econometrics one often assumes that an observed series of data values is the sum of a series of values generated by a deterministic linear process, depending on certain independent (explanatory) variables, and on a series of random noise values. Then regression analysis is used to infer the parameters of the model process from the observed data, e.g. by ordinary least squares, and to test the null hypothesis that each of the parameters is zero against the alternative hypothesis that it is non-zero. Hypothesis testing typically assumes that the noise values are mutually uncorrelated with zero mean and have the same Gaussian probability distributionin other words, that the noise is Gaussian white (not just white). If there is non-zero correlation between the noise values underlying different observations then the estimated model parameters are still unbiased, but estimates of their uncertainties (such as confidence intervals) will be biased (not accurate on average). This is also true if the noise is heteroskedasticthat is, if it has different variances for different data points.

Alternatively, in the subset of regression analysis known as time series analysis there are often no explanatory variables other than the past values of the variable being modeled (the dependent variable). In this case the noise process is often modeled as a moving average process, in which the current value of the dependent variable depends on current and past values of a sequential white noise process.

Random vector transformations

These two ideas are crucial in applications such as channel estimation and channel equalization in communications and audio. These concepts are also used in data compression.

In particular, by a suitable linear transformation (a coloring transformation), a white random vector can be used to produce a "non-white" random vector (that is, a list of random variables) whose elements have a prescribed covariance matrix. Conversely, a random vector with known covariance matrix can be transformed into a white random vector by a suitable whitening transformation.

Generation

White noise may be generated digitally with a digital signal processor, microprocessor, or microcontroller. Generating white noise typically entails feeding an appropriate stream of random numbers to a digital-to-analog converter. The quality of the white noise will depend on the quality of the algorithm used.

Informal use

The term is sometimes used as a colloquialism to describe a backdrop of ambient sound, creating an indistinct or seamless commotion. Following are some examples:

*Chatter from multiple conversations within the acoustics of a confined space.
*The pleonastic jargon used by politicians to mask a point that they don't want noticed.
* Music that is disagreeable, harsh, dissonant or discordant with no melody.

The term can also be used metaphorically, as in the novel '' White Noise'' (1985) by Don DeLillo which explores the symptoms of modern culture that came together so as to make it difficult for an individual to actualize their ideas and personality.

See also

References

External links

{{DEFAULTSORT:White Noise
Noise (electronics)
Statistical signal processing
Data compression
Sound
Acoustics