Watt's Curve

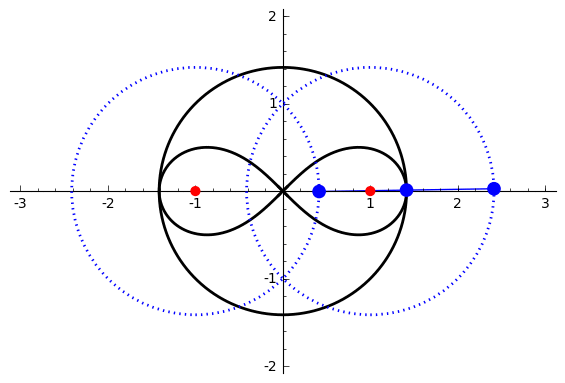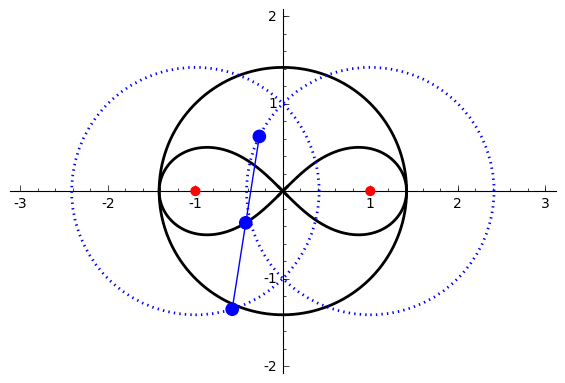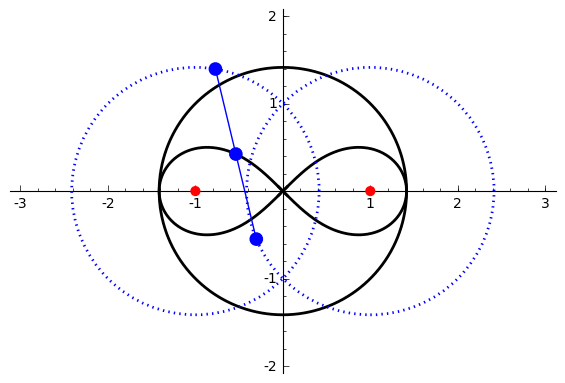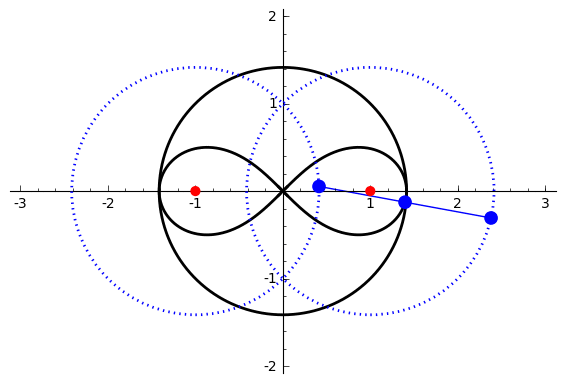In mathematics, Watt's curve is a tricircular plane algebraic curve of degree six. It is generated by two circles of radius ''b'' with centers distance 2''a'' apart (taken to be at (±''a'', 0)). A line segment of length 2''c'' attaches to a point on each of the circles, and the midpoint of the line segment traces out the Watt curve as the circles rotate partially back and forth or completely around. It arose in connection with James Watt's pioneering work on the steam engine.

The equation of the curve can be given in polar coordinates as
:r^2=b^2-\left \sin\theta\pm\sqrt\right2.

Derivation

Polar coordinates

The polar equation for the curve can be derived as follows:
Working in the complex plane, let the centers of the circles be at ''a'' and ''−a'', and the connecting segment have endpoints at ''−a''+''be''^''i'' λ and ''a''+''be''^{''i'' ρ}. Let the angle of inclination of the segment be ψ with its midpoint at ''re''^{''i'' θ}. Then the endpoints are also given by ''re''^{''i'' θ} ± ''ce''^{''i'' ψ}. Setting expressions for the same points equal to each other gives
:$a+be^=re^+ce^.\,$
:$-a+be^=re^-ce^\,$
Add these and divide by two to get
:$re^=\tfrac(e^+e^)=b\cos(\tfrac)e^.$
Comparing radii and arguments gives
:$r=b\cos\alpha,\ \theta=\tfrac\ \mbox\ \alpha=\tfrac.$
Similarly, subtracting the first two equations and dividing by 2 gives
:$ce^-a=\tfrac(e^-e^)=i b\sin\alpha e^.$
Write
:$a=a\cos\theta\ e^ - i a\sin\theta\ e^.\,$
Then
:$ce^=i b\sin\alpha e^+a\cos\theta\ e^ - i a\sin\theta\ e^=(a\cos\theta\ +i(b\sin\alpha-a\sin\theta))e^,$
:$c^2=a^2\cos^2\theta+(b\sin\alpha-a\sin\theta)^2,\,$
:$b\sin\alpha=a\sin\theta\pm\sqrt,\,$
:r^2=b^2\cos^2\alpha=b^2-b^2\sin^2\alpha=b^2-\left \sin\theta\pm\sqrt\right2.,\,

Cartesian coordinates

Expanding the polar equation gives
:$r^2=b^2-(a^2\sin^2\theta\ + c^2-a^2\cos^2\theta \pm 2a\sin\theta\sqrt),\,$
:$r^2-a^2-b^2+c^2+2a^2\sin^2\theta=\pm 2a\sin\theta\sqrt),\,$
:$(r^2-a^2-b^2+c^2)^2+4a^2(r^2-a^2-b^2+c^2)\sin^2\theta+4a^4\sin^4\theta=4a^2\sin^2\theta(c^2-a^2\cos^2\theta),\,$
:$(r^2-a^2-b^2+c^2)^2+4a^2(r^2-b^2)\sin^2\theta=0,\,$
:$(x^2+y^2)(x^2+y^2-a^2-b^2+c^2)^2+4a^2y^2(x^2+y^2-b^2)=0.\,$
Letting ''d'' ²=''a''²+''b''²–''c''² simplifies this to
:$(x^2+y^2)(x^2+y^2-d^2)^2+4a^2y^2(x^2+y^2-b^2)=0.\,$

Form of the curve

The construction requires a quadrilateral with sides 2''a'', ''b'', 2''c'', ''b''. Any side must be less than the sum of the remaining sides, so the curve is empty (at least in the real plane) unless ''a''<''b''+''c'' and ''c''<''b''+''a''.

The curve has a crossing point at the origin if there is a triangle with sides ''a'', ''b'' and ''c''. Given the previous conditions, this means that the curve crosses the origin if and only if ''b''<''a''+''c''. If ''b''=''a''+''c'' then two branches of the curve meet at the origin with a common vertical tangent, making it a quadruple point.

Given ''b''<''a''+''c'', the shape of the curve is determined by the relative magnitude of ''b'' and ''d''. If ''d'' is imaginary, that is if ''a''²+''b''² <''c''² then the curve has the form of a figure eight. If ''d'' is 0 then the curve is a figure eight with two branches of the curve having a common horizontal tangent at the origin. If 0<''d''<''b'' then the curve has two additional double points at ±''d'' and the curve crosses itself at these points. The overall shape of the curve is pretzel-like in this case. If ''d''=''b'' then ''a''=''c'' and the curve decomposes into a circle of radius ''b'' and a lemniscate of Booth, a figure eight shaped curve. A special case of this is ''a''=''c'', ''b''=√2''c'' which produces the lemniscate of Bernoulli. Finally, if ''d''>''b'' then the points ±''d'' are still solutions to the Cartesian equation of the curve, but the curve does not cross these points and they are acnodes. The curve again has a figure eight shape though the shape is distorted if ''d'' is close to ''b''.

Given ''b''>''a''+''c'', the shape of the curve is determined by the relative sizes of ''a'' and ''c''. If ''a''<''c'' then the curve has the form of two loops that cross each other at ±''d''. If ''a''=''c'' then the curve decomposes into a circle of radius ''b'' and an oval of Booth. If ''a''>''c'' then the curve does not cross the ''x''-axis at all and consists of two flattened ovals.Encyclopédie des Formes Mathématiques Remarquables page for section.

Watt's linkage

When the curve crosses the origin, the origin is a point of inflection and therefore has contact of order 3 with a tangent. However, if $a^2=b^2+c^2$ ( which is the case if the triangle with sides $a$, $b$ and $c$ is a right triangle) then tangent has contact of order 5 with the tangent, in other words the curve is a close approximation of a straight line. This is the basis for Watt's linkage.

See also

* Four-bar linkage
* Watt's linkage

References

External links

*
*
*
*

{{DEFAULTSORT:Watt's Curve
Sextic curves
Curve