Tychonoff space on:
[Wikipedia]
[Google]
[Amazon]
In
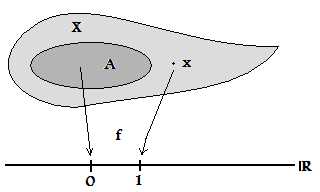 A topological space is called if points can be separated from closed sets via (bounded) continuous real-valued functions. In technical terms this means: for any
A topological space is called if points can be separated from closed sets via (bounded) continuous real-valued functions. In technical terms this means: for any
topology
In mathematics, topology (from the Greek words , and ) is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing ...
and related branches of mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, Tychonoff spaces and completely regular spaces are kinds of topological space
In mathematics, a topological space is, roughly speaking, a geometrical space in which closeness is defined but cannot necessarily be measured by a numeric distance. More specifically, a topological space is a set whose elements are called poin ...
s. These conditions are examples of separation axiom
In topology and related fields of mathematics, there are several restrictions that one often makes on the kinds of topological spaces that one wishes to consider. Some of these restrictions are given by the separation axioms. These are sometim ...
s. A Tychonoff space refers to any completely regular space that is also a Hausdorff space
In topology and related branches of mathematics, a Hausdorff space ( , ), separated space or T2 space is a topological space where, for any two distinct points, there exist neighbourhoods of each which are disjoint from each other. Of the ma ...
; there exist completely regular spaces that are not Tychonoff (i.e. not Hausdorff).
Tychonoff spaces are named after Andrey Nikolayevich Tychonoff
Andrey Nikolayevich Tikhonov (russian: Андре́й Никола́евич Ти́хонов; October 17, 1906 – October 7, 1993) was a leading Soviet Russian mathematician and geophysicist known for important contributions to topology, ...
, whose Russian name (Тихонов) is variously rendered as "Tychonov", "Tikhonov", "Tihonov", "Tichonov", etc. who introduced them in 1930 in order to avoid the pathological situation of Hausdorff space
In topology and related branches of mathematics, a Hausdorff space ( , ), separated space or T2 space is a topological space where, for any two distinct points, there exist neighbourhoods of each which are disjoint from each other. Of the ma ...
s whose only continuous real-valued functions are constant maps.
Definitions
 A topological space is called if points can be separated from closed sets via (bounded) continuous real-valued functions. In technical terms this means: for any
A topological space is called if points can be separated from closed sets via (bounded) continuous real-valued functions. In technical terms this means: for any closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points. In a complete metric space, a ...
and any point there exists a real-valued continuous function
In mathematics, a continuous function is a function such that a continuous variation (that is a change without jump) of the argument induces a continuous variation of the value of the function. This means that there are no abrupt changes in val ...
such that and (Equivalently one can choose any two values instead of and and even demand that be a bounded function.)
A topological space is called a (alternatively: , or , or ) if it is a completely regular Hausdorff space
In topology and related branches of mathematics, a Hausdorff space ( , ), separated space or T2 space is a topological space where, for any two distinct points, there exist neighbourhoods of each which are disjoint from each other. Of the ma ...
.
Remark. Completely regular spaces and Tychonoff spaces are related through the notion of Kolmogorov equivalence. A topological space is Tychonoff if and only if it's both completely regular and T0. On the other hand, a space is completely regular if and only if its Kolmogorov quotient is Tychonoff.
Naming conventions
Across mathematical literature different conventions are applied when it comes to the term "completely regular" and the "T"-Axioms. The definitions in this section are in typical modern usage. Some authors, however, switch the meanings of the two kinds of terms, or use all terms interchangeably. In Wikipedia, the terms "completely regular" and "Tychonoff" are used freely and the "T"-notation is generally avoided. In standard literature, caution is thus advised, to find out which definitions the author is using. For more on this issue, see History of the separation axioms.Examples and counterexamples
Almost every topological space studied inmathematical analysis
Analysis is the branch of mathematics dealing with continuous functions, limits, and related theories, such as differentiation, integration, measure, infinite sequences, series, and analytic functions.
These theories are usually studied ...
is Tychonoff, or at least completely regular.
For example, the real line
In elementary mathematics, a number line is a picture of a graduated straight line that serves as visual representation of the real numbers. Every point of a number line is assumed to correspond to a real number, and every real number to a po ...
is Tychonoff under the standard Euclidean topology
In mathematics, and especially general topology, the Euclidean topology is the natural topology induced on n-dimensional Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, ...
.
Other examples include:
* Every metric space
In mathematics, a metric space is a set together with a notion of '' distance'' between its elements, usually called points. The distance is measured by a function called a metric or distance function. Metric spaces are the most general setti ...
is Tychonoff; every pseudometric space is completely regular.
* Every locally compact In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space. More precisely, it is a topological space in which ev ...
regular space
In topology and related fields of mathematics, a topological space ''X'' is called a regular space if every closed subset ''C'' of ''X'' and a point ''p'' not contained in ''C'' admit non-overlapping open neighborhoods. Thus ''p'' and ''C'' ca ...
is completely regular, and therefore every locally compact Hausdorff space is Tychonoff.
* In particular, every topological manifold is Tychonoff.
* Every totally ordered set
In mathematics, a total or linear order is a partial order in which any two elements are comparable. That is, a total order is a binary relation \leq on some set X, which satisfies the following for all a, b and c in X:
# a \leq a ( reflexive) ...
with the order topology is Tychonoff.
* Every topological group
In mathematics, topological groups are logically the combination of groups and topological spaces, i.e. they are groups and topological spaces at the same time, such that the continuity condition for the group operations connects these two st ...
is completely regular.
* Generalizing both the metric spaces and the topological groups, every uniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure that is used to define uniform properties such as completeness, uniform continuity and unifo ...
is completely regular. The converse is also true: every completely regular space is uniformisable.
* Every CW complex
A CW complex (also called cellular complex or cell complex) is a kind of a topological space that is particularly important in algebraic topology. It was introduced by J. H. C. Whitehead (open access) to meet the needs of homotopy theory. This cl ...
is Tychonoff.
* Every normal regular space is completely regular, and every normal Hausdorff space is Tychonoff.
* The Niemytzki plane is an example of a Tychonoff space that is not normal.
Properties
Preservation
Complete regularity and the Tychonoff property are well-behaved with respect to initial topologies. Specifically, complete regularity is preserved by taking arbitrary initial topologies and the Tychonoff property is preserved by taking point-separating initial topologies. It follows that: * Every subspace of a completely regular or Tychonoff space has the same property. * A nonempty product space is completely regular (respectively Tychonoff) if and only if each factor space is completely regular (respectively Tychonoff). Like all separation axioms, complete regularity is not preserved by taking final topologies. In particular, quotients of completely regular spaces need not be regular. Quotients of Tychonoff spaces need not even be Hausdorff, with one elementary counterexample being the bug-eyed line. There are closed quotients of the Moore plane that provide counterexamples.Real-valued continuous functions
For any topological space let denote the family of real-valued continuous functions on and let be the subset of bounded real-valued continuous functions. Completely regular spaces can be characterized by the fact that their topology is completely determined by or In particular: * A space is completely regular if and only if it has theinitial topology
In general topology and related areas of mathematics, the initial topology (or induced topology or weak topology or limit topology or projective topology) on a set X, with respect to a family of functions on X, is the coarsest topology on ''X'' t ...
induced by or
* A space is completely regular if and only if every closed set can be written as the intersection of a family of zero sets in (i.e. the zero sets form a basis for the closed sets of ).
* A space is completely regular if and only if the cozero sets of form a basis for the topology of
Given an arbitrary topological space there is a universal way of associating a completely regular space with Let ρ be the initial topology on induced by or, equivalently, the topology generated by the basis of cozero sets in Then ρ will be the finest completely regular topology on that is coarser than This construction is universal
Universal is the adjective for universe.
Universal may also refer to:
Companies
* NBCUniversal, a media and entertainment company
** Universal Animation Studios, an American Animation studio, and a subsidiary of NBCUniversal
** Universal TV, a t ...
in the sense that any continuous function
to a completely regular space will be continuous on In the language of category theory
Category theory is a general theory of mathematical structures and their relations that was introduced by Samuel Eilenberg and Saunders Mac Lane in the middle of the 20th century in their foundational work on algebraic topology. Nowadays, ca ...
, the functor that sends to is left adjoint to the inclusion functor CReg → Top. Thus the category of completely regular spaces CReg is a reflective subcategory
In mathematics, a full subcategory ''A'' of a category ''B'' is said to be reflective in ''B'' when the inclusion functor from ''A'' to ''B'' has a left adjoint. This adjoint is sometimes called a ''reflector'', or ''localization''. Dually, ''A' ...
of Top, the category of topological spaces In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again cont ...
. By taking Kolmogorov quotients, one sees that the subcategory of Tychonoff spaces is also reflective.
One can show that in the above construction so that the rings and are typically only studied for completely regular spaces
The category of realcompact Tychonoff spaces is anti-equivalent to the category of the rings (where is realcompact) together with ring homomorphisms as maps. For example one can reconstruct from when is (real) compact. The algebraic theory of these rings is therefore subject of intensive studies.
A vast generalization of this class of rings that still resembles many properties of Tychonoff spaces, but is also applicable in real algebraic geometry, is the class of real closed ring In mathematics, a real closed ring (RCR) is a commutative ring ''A'' that is a subring of a product of real closed fields, which is closed under continuous semi-algebraic functions defined over the integers.
Examples of real closed rings
Since ...
s.
Embeddings
Tychonoff spaces are precisely those spaces that can be embedded in compact Hausdorff spaces. More precisely, for every Tychonoff space there exists a compact Hausdorff space such that ishomeomorphic
In the mathematical field of topology, a homeomorphism, topological isomorphism, or bicontinuous function is a bijective and continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomor ...
to a subspace of
In fact, one can always choose to be a Tychonoff cube (i.e. a possibly infinite product of unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1. It is often denoted ' (capital letter ). In addition to its role in real analysis ...
s). Every Tychonoff cube is compact Hausdorff as a consequence of Tychonoff's theorem. Since every subspace of a compact Hausdorff space is Tychonoff one has:
:''A topological space is Tychonoff if and only if it can be embedded in a Tychonoff cube''.
Compactifications
Of particular interest are those embeddings where the image of is dense in these are called Hausdorff compactifications of Given any embedding of a Tychonoff space in a compact Hausdorff space the closure of the image of in is a compactification of In the same 1930 article where Tychonoff defined completely regular spaces, he also proved that every Tychonoff space has a Hausdorff compactification. Among those Hausdorff compactifications, there is a unique "most general" one, the Stone–Čech compactification It is characterized by theuniversal property
In mathematics, more specifically in category theory, a universal property is a property that characterizes up to an isomorphism the result of some constructions. Thus, universal properties can be used for defining some objects independently fr ...
that, given a continuous map from to any other compact Hausdorff space there is a unique continuous map that extends in the sense that is the composition of and
Uniform structures
Complete regularity is exactly the condition necessary for the existence of uniform structures on a topological space. In other words, everyuniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure that is used to define uniform properties such as completeness, uniform continuity and unifo ...
has a completely regular topology and every completely regular space is uniformizable. A topological space admits a separated uniform structure if and only if it is Tychonoff.
Given a completely regular space there is usually more than one uniformity on that is compatible with the topology of However, there will always be a finest compatible uniformity, called the fine uniformity on If is Tychonoff, then the uniform structure can be chosen so that becomes the completion of the uniform space
See also
*Citations
Bibliography
* * * {{refend Separation axioms Topological spaces Topology