Turing Degree

In computer science and mathematical logic the Turing degree (named after Alan Turing) or degree of unsolvability of a set of natural numbers measures the level of algorithmic unsolvability of the set.

Overview

The concept of Turing degree is fundamental in computability theory, where sets of natural numbers are often regarded as decision problems. The Turing degree of a set is a measure of how difficult it is to solve the decision problem associated with the set, that is, to determine whether an arbitrary number is in the given set.

Two sets are Turing equivalent if they have the same level of unsolvability; each Turing degree is a collection of Turing equivalent sets, so that two sets are in different Turing degrees exactly when they are not Turing equivalent. Furthermore, the Turing degrees are partially ordered, so that if the Turing degree of a set ''X'' is less than the Turing degree of a set ''Y'', then any (noncomputable) procedure that correctly decides whether numbers are in ''Y'' can be effectively converted to a procedure that correctly decides whether numbers are in ''X''. It is in this sense that the Turing degree of a set corresponds to its level of algorithmic unsolvability.

The Turing degrees were introduced by Emil Leon Post (1944), and many fundamental results were established by Stephen Cole Kleene and Post (1954). The Turing degrees have been an area of intense research since then. Many proofs in the area make use of a proof technique known as the priority method.

Turing equivalence

For the rest of this article, the word ''set'' will refer to a set of natural numbers. A set ''X'' is said to be Turing reducible to a set ''Y'' if there is an oracle Turing machine that decides membership in ''X'' when given an oracle for membership in ''Y''. The notation ''X'' ≤_T ''Y'' indicates that ''X'' is Turing reducible to ''Y''.

Two sets ''X'' and ''Y'' are defined to be Turing equivalent if ''X'' is Turing reducible to ''Y'' and ''Y'' is Turing reducible to ''X''. The notation ''X'' ≡_T ''Y'' indicates that ''X'' and ''Y'' are Turing equivalent. The relation ≡_T can be seen to be an equivalence relation, which means that for all sets ''X'', ''Y'', and ''Z'':
* ''X'' ≡_T ''X''
* ''X'' ≡_T ''Y'' implies ''Y'' ≡_T ''X''
* If ''X'' ≡_T ''Y'' and ''Y'' ≡_T ''Z'' then ''X'' ≡_T ''Z''.

A Turing degree is an equivalence class of the relation ≡_T. The notation 'X''denotes the equivalence class containing a set ''X''. The entire collection of Turing degrees is denoted $\mathcal$.

The Turing degrees have a partial order ≤ defined so that 'X''≤ 'Y''if and only if ''X'' ≤_T ''Y''. There is a unique Turing degree containing all the computable sets, and this degree is less than every other degree. It is denoted 0 (zero) because it is the least element of the poset $\mathcal$. (It is common to use boldface notation for Turing degrees, in order to distinguish them from sets. When no confusion can occur, such as with 'X'' the boldface is not necessary.)

For any sets ''X'' and ''Y'', X join Y, written ''X'' ⊕ ''Y'', is defined to be the union of the sets and . The Turing degree of ''X'' ⊕ ''Y'' is the least upper bound of the degrees of ''X'' and ''Y''. Thus $\mathcal$ is a join-semilattice. The least upper bound of degrees a and b is denoted a ∪ b. It is known that $\mathcal$ is not a lattice, as there are pairs of degrees with no greatest lower bound.

For any set ''X'' the notation ''X''′ denotes the set of indices of oracle machines that halt (when given their index as input) when using ''X'' as an oracle. The set ''X''′ is called the Turing jump of ''X''. The Turing jump of a degree 'X''is defined to be the degree 'X''′ this is a valid definition because ''X''′ ≡_T ''Y''′ whenever ''X'' ≡_T ''Y''. A key example is 0′, the degree of the halting problem.

Basic properties of the Turing degrees

* Every Turing degree is countably infinite, that is, it contains exactly $\aleph_0$ sets.
* There are $2^$ distinct Turing degrees.
* For each degree a the strict inequality a < a′ holds.
* For each degree a, the set of degrees below a is countable. The set of degrees greater than a has size $2^$.

Structure of the Turing degrees

A great deal of research has been conducted into the structure of the Turing degrees. The following survey lists only some of the many known results. One general conclusion that can be drawn from the research is that the structure of the Turing degrees is extremely complicated.

Order properties

* There are minimal degrees. A degree a is ''minimal'' if a is nonzero and there is no degree between 0 and a. Thus the order relation on the degrees is not a dense order.
* The Turing degrees are not linearly ordered by ≤_T.
* In fact, for every nonzero degree a there is a degree b incomparable with a.
* There is a set of $2^$ pairwise incomparable Turing degrees.
* There are pairs of degrees with no greatest lower bound. Thus $\mathcal$ is not a lattice.
* Every countable partially ordered set can be embedded in the Turing degrees.
* An infinite strictly increasing sequence a₁, a₂, ... of Turing degrees cannot have the least upper bound, but it always has an ''exact pair'' c, d such that ∀e (e<c∧e<d ⇔ ∃''i'' e≤a_''i''), and thus it has (non-unique) minimal upper bounds.
* Assuming the axiom of constructibility, it can be shown there is a maximal chain of degrees of order type $\omega_1$.C. T. Chong, L. Yu
Maximal Chains in the Turing Degrees
''The Journal of Symbolic Logic'' Vol. 72, No. 4 (Dec., 2007), p.1224.

Properties involving the jump

* For every degree a there is a degree strictly between a and a′. In fact, there is a countable family of pairwise incomparable degrees between a and a′.
* Jump inversion: a degree a is of the form b′ if and only if 0′ ≤ a.
* For any degree a there is a degree b such that a < b and b′ = a′; such a degree b is called ''low'' relative to a.
* There is an infinite sequence a_''i'' of degrees such that a′_''i''+1 ≤ a_''i'' for each ''i''.
* Post's theorem, establishing a close correspondence between the arithmetical hierarchy and finitely iterated Turing jumps of the empty set

Logical properties

* Simpson (1977) showed that the first-order theory of $\mathcal$ in the language or is many-one equivalent to the theory of true second-order arithmetic. This indicates that the structure of $\mathcal$ is extremely complicated.
* Shore and Slaman (1999) showed that the jump operator is definable in the first-order structure of $\mathcal$ with the language .

Recursively enumerable Turing degrees

A degree is called ''recursively enumerable'' (r.e.) or ''computably enumerable'' (c.e.) if it contains a recursively enumerable set. Every r.e. degree is below 0′, but not every degree below 0′ is r.e..

* ( G. E. Sacks, 1964) The r.e. degrees are dense; between any two r.e. degrees there is a third r.e. degree.
* (A. H. Lachlan, 1966a and C. E. M. Yates, 1966) There are two r.e. degrees with no greatest lower bound in the r.e. degrees.
* (A. H. Lachlan, 1966a and C. E. M. Yates, 1966) There is a pair of nonzero r.e. degrees whose greatest lower bound is 0.
* (A. H. Lachlan, 1966b) There is no pair of r.e. degrees whose greatest lower bound is 0 and whose least upper bound is 0′. This result is informally called the ''nondiamond theorem''.
* (S. K. Thomason, 1971) Every finite distributive lattice can be embedded into the r.e. degrees. In fact, the countable atomless Boolean algebra can be embedded in a manner that preserves suprema and infima.
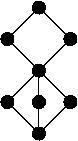
* (A. H. Lachlan and R. I. Soare, 1980) Not all finite lattices can be embedded in the r.e. degrees (via an embedding that preserves suprema and infima). A particular example is shown to the right.
* ( L. A. Harrington and T. A. Slaman, see Nies, Shore, and Slaman (1998)) The first-order theory of the r.e. degrees in the language ⟨ 0, ≤, = ⟩ is many-one equivalent to the theory of true first-order arithmetic.

Post's problem and the priority method

Emil Post studied the r.e. Turing degrees and asked whether there is any r.e. degree strictly between 0 and 0′. The problem of constructing such a degree (or showing that none exist) became known as Post's problem. This problem was solved independently by Friedberg and Muchnik in the 1950s, who showed that these intermediate r.e. degrees do exist ( Friedberg–Muchnik theorem). Their proofs each developed the same new method for constructing r.e. degrees, which came to be known as the priority method. The priority method is now the main technique for establishing results about r.e. sets.

The idea of the priority method for constructing a r.e. set ''X'' is to list a countable sequence of ''requirements'' that ''X'' must satisfy. For example, to construct a r.e. set ''X'' between 0 and 0′ it is enough to satisfy the requirements ''A_e'' and ''B_e'' for each natural number ''e'', where ''A_e'' requires that the oracle machine with index ''e'' does not compute 0′ from ''X'' and ''B_e'' requires that the Turing machine with index ''e'' (and no oracle) does not compute ''X''. These requirements are put into a ''priority ordering'', which is an explicit bijection of the requirements and the natural numbers. The proof proceeds inductively with one stage for each natural number; these stages can be thought of as steps of time during which the set ''X'' is enumerated. At each stage, numbers may be put into ''X'' or forever (if not injured) prevented from entering ''X'' in an attempt to ''satisfy'' requirements (that is, force them to hold once all of ''X'' has been enumerated). Sometimes, a number can be enumerated into ''X'' to satisfy one requirement but doing this would cause a previously satisfied requirement to become unsatisfied (that is, to be ''injured''). The priority order on requirements is used to determine which requirement to satisfy in this case. The informal idea is that if a requirement is injured then it will eventually stop being injured after all higher priority requirements have stopped being injured, although not every priority argument has this property. An argument must be made that the overall set ''X'' is r.e. and satisfies all the requirements. Priority arguments can be used to prove many facts about r.e. sets; the requirements used and the manner in which they are satisfied must be carefully chosen to produce the required result.

For example, a simple (and hence noncomputable r.e.) low ''X'' (low means ''X''′=0′) can be constructed in infinitely many stages as follows. At the start of stage ''n'', let ''T''_''n'' be the output (binary) tape, identified with the set of cell indices where we placed 1 so far (so ''X''=∪_''n'' ''T''_''n''; ''T''₀=∅); and let ''P''_''n''(''m'') be the priority for not outputting 1 at location ''m''; ''P''₀(''m'')=∞. At stage ''n'', if possible (otherwise do nothing in the stage), pick the least ''i''<''n'' such that ∀''m'' ''P''_''n''(''m'')≠''i'' and Turing machine ''i'' halts in <''n'' steps on some input ''S''⊇''T''_''n'' with ∀''m''∈''S''\''T''_''n'' ''P''_''n''(''m'')≥''i''. Choose any such (finite) ''S'', set ''T''_''n''+1=''S'', and for every cell ''m'' visited by machine ''i'' on ''S'', set ''P''_''n''+1(''m'') = min(''i'', ''P''_''n''(''m'')), and set all priorities >''i'' to ∞, and then set one priority ∞ cell (any will do) not in ''S'' to priority ''i''. Essentially, we make machine ''i'' halt if we can do so without upsetting priorities <''i'', and then set priorities to prevent machines >''i'' from disrupting the halt; all priorities are eventually constant.

To see that ''X'' is low, machine ''i'' halts on ''X'' iff it halts in <''n'' steps on some ''T''_''n'' such that machines <''i'' that halt on ''X'' do so <''n''-''i'' steps (by recursion, this is uniformly computable from 0′). ''X'' is noncomputable since otherwise a Turing machine could halt on ''Y'' iff ''Y''\''X'' is nonempty, contradicting the construction since ''X'' excludes some priority ''i'' cells for arbitrarily large ''i''; and ''X'' is simple because for each ''i'' the number of priority ''i'' cells is finite.

See also

* Martin measure

References

;Monographs (undergraduate level)
* Cooper, S.B. ''Computability theory''. Chapman & Hall/CRC, Boca Raton, FL, 2004.
* Cutland, N. ''Computability.'' Cambridge University Press, Cambridge-New York, 1980. ;

;Monographs and survey articles (graduate level)
* Ambos-Spies, K. and Fejer, P. Degrees of Unsolvability. Unpublished. http://www.cs.umb.edu/~fejer/articles/History_of_Degrees.pdf
* Lerman, M. ''Degrees of unsolvability.'' Perspectives in Mathematical Logic. Springer-Verlag, Berlin, 1983.
*
*
* Rogers, H. ''The Theory of Recursive Functions and Effective Computability'', MIT Press. ,
* Sacks, Gerald E. ''Degrees of Unsolvability'' (Annals of Mathematics Studies), Princeton University Press.
* Simpson, S. Degrees of unsolvability: a survey of results. ''Handbook of Mathematical Logic'', North-Holland, 1977, pp. 631–652.
* Shoenfield, Joseph R. ''Degrees of Unsolvability'', North-Holland/Elsevier, .
*
* Soare, R. ''Recursively enumerable sets and degrees.'' Perspectives in Mathematical Logic. Springer-Verlag, Berlin, 1987.
* Soare, Robert I. Recursively enumerable sets and degrees. ''Bull. Amer. Math. Soc.'' 84 (1978), no. 6, 1149–1181.

;Research papers
*
*
*
*
*
*
*
*
*
*
*

;Inline citations

{{Alan Turing

Computability theory
Theory of computation
Alan Turing