Towers of Hanoi on:
[Wikipedia]
[Google]
[Amazon]


 The Tower of Hanoi (also called The problem of Benares Temple or Tower of Brahma or Lucas' Tower and sometimes pluralized as Towers, or simply pyramid puzzle) is a mathematical game or
The Tower of Hanoi (also called The problem of Benares Temple or Tower of Brahma or Lucas' Tower and sometimes pluralized as Towers, or simply pyramid puzzle) is a mathematical game or
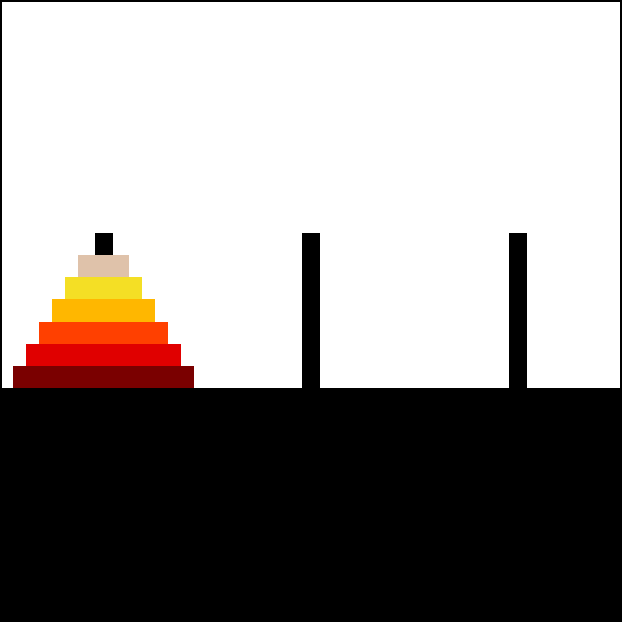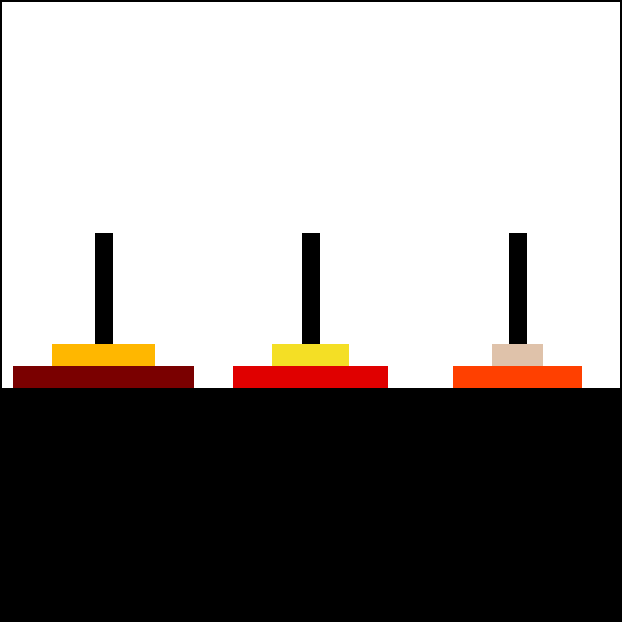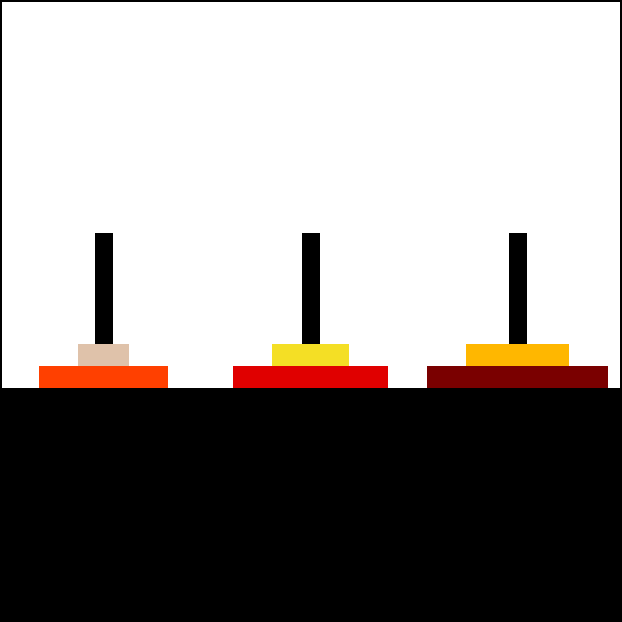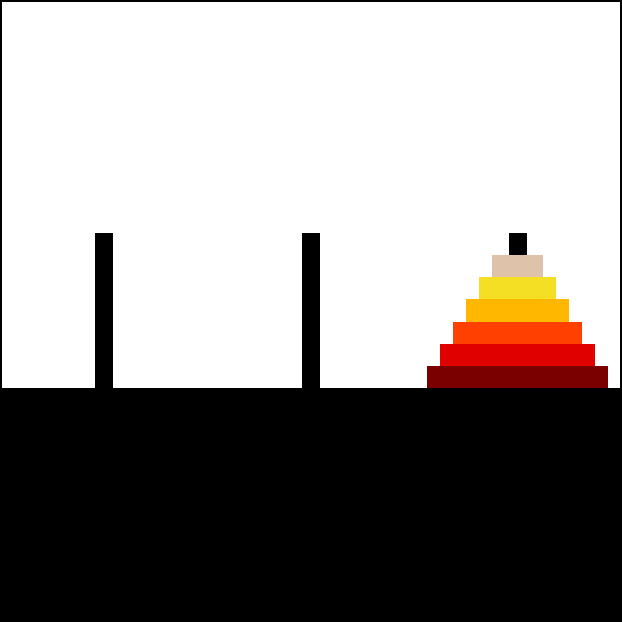 A simple solution for the toy puzzle is to alternate moves between the smallest piece and a non-smallest piece. When moving the smallest piece, always move it to the next position in the same direction (to the right if the starting number of pieces is even, to the left if the starting number of pieces is odd). If there is no tower position in the chosen direction, move the piece to the opposite end, but then continue to move in the correct direction. For example, if you started with three pieces, you would move the smallest piece to the opposite end, then continue in the left direction after that. When the turn is to move the non-smallest piece, there is only one legal move. Doing this will complete the puzzle in the fewest moves.
A simple solution for the toy puzzle is to alternate moves between the smallest piece and a non-smallest piece. When moving the smallest piece, always move it to the next position in the same direction (to the right if the starting number of pieces is even, to the left if the starting number of pieces is odd). If there is no tower position in the chosen direction, move the piece to the opposite end, but then continue to move in the correct direction. For example, if you started with three pieces, you would move the smallest piece to the opposite end, then continue in the left direction after that. When the turn is to move the non-smallest piece, there is only one legal move. Doing this will complete the puzzle in the fewest moves.
 The key to solving a problem recursively is to recognize that it can be broken down into a collection of smaller sub-problems, to each of which ''that same general solving procedure that we are seeking'' applies, and the total solution is then found in some ''simple'' way from those sub-problems' solutions. Each of these created sub-problems being "smaller" guarantees that the base case(s) will eventually be reached. Thence, for the Towers of Hanoi:
* label the pegs A, B, C,
* let ''n'' be the total number of disks,
* number the disks from 1 (smallest, topmost) to ''n'' (largest, bottom-most).
Assuming all ''n'' disks are distributed in valid arrangements among the pegs; assuming there are ''m'' top disks on a ''source'' peg, and all the rest of the disks are larger than ''m'', so they can be safely ignored; to move ''m'' disks from a source peg to a ''target'' peg using a ''spare'' peg, without violating the rules:
# Move ''m'' − 1 disks from the source to the spare peg, by ''the same general solving procedure''. Rules are not violated, by assumption. This leaves the disk ''m'' as a top disk on the source peg.
# Move the disk ''m'' from the source to the target peg, which is guaranteed to be a valid move, by the assumptions — ''a simple step''.
# Move the ''m'' − 1 disks that we have just placed on the spare, from the spare to the target peg by ''the same general solving procedure'', so they are placed on top of the disk ''m'' without violating the rules.
# The base case is to move ''0'' disks (in steps 1 and 3), that is, do nothing – which obviously doesn't violate the rules.
The full Tower of Hanoi solution then consists of moving ''n'' disks from the source peg A to the target peg C, using B as the spare peg.
This approach can be given a rigorous mathematical proof with
The key to solving a problem recursively is to recognize that it can be broken down into a collection of smaller sub-problems, to each of which ''that same general solving procedure that we are seeking'' applies, and the total solution is then found in some ''simple'' way from those sub-problems' solutions. Each of these created sub-problems being "smaller" guarantees that the base case(s) will eventually be reached. Thence, for the Towers of Hanoi:
* label the pegs A, B, C,
* let ''n'' be the total number of disks,
* number the disks from 1 (smallest, topmost) to ''n'' (largest, bottom-most).
Assuming all ''n'' disks are distributed in valid arrangements among the pegs; assuming there are ''m'' top disks on a ''source'' peg, and all the rest of the disks are larger than ''m'', so they can be safely ignored; to move ''m'' disks from a source peg to a ''target'' peg using a ''spare'' peg, without violating the rules:
# Move ''m'' − 1 disks from the source to the spare peg, by ''the same general solving procedure''. Rules are not violated, by assumption. This leaves the disk ''m'' as a top disk on the source peg.
# Move the disk ''m'' from the source to the target peg, which is guaranteed to be a valid move, by the assumptions — ''a simple step''.
# Move the ''m'' − 1 disks that we have just placed on the spare, from the spare to the target peg by ''the same general solving procedure'', so they are placed on top of the disk ''m'' without violating the rules.
# The base case is to move ''0'' disks (in steps 1 and 3), that is, do nothing – which obviously doesn't violate the rules.
The full Tower of Hanoi solution then consists of moving ''n'' disks from the source peg A to the target peg C, using B as the spare peg.
This approach can be given a rigorous mathematical proof with
A =
_
In_discrete_mathematics,_and_more_specifically_in_graph_theory,_a_graph_is_a_structure_amounting_to_a_set_of_objects_in_which_some_pairs_of_the_objects_are_in_some_sense_"related"._The_objects_correspond_to_mathematical_abstractions_called_''_ve_...
,_the_nodes_representing_distributions_of_disks_and_the_edges_representing_moves._For_one_disk,_the_graph_is_a_triangle:
file:tower_of_hanoi_graph.svg.html" ;"title="Graph_(discrete_mathematics)#Undirected_graph.html" "title="^8_-_1">ange[2^8_-_1_2.html" ;"title="^8_-_1.html" ;"title="ange[2^8 - 1">ange[2^8 - 1 2">^8_-_1.html" ;"title="ange[2^8 - 1">ange[2^8 - 1 2+ 1 gives moves for the 8-disk puzzle.
, the nodes representing distributions of disks and the edges representing moves. For one disk, the graph is a triangle:
file:tower_of_hanoi_graph.svg">lang=simple, 120px, center
The graph for two disks is three triangles connected to form the corners of a larger triangle.
A second letter is added to represent the larger disk. Clearly, it cannot initially be moved.
The topmost small triangle now represents the one-move possibilities with two disks:
file:tower_of_hanoi_graph.svg, lang=tw, 200px, center
The nodes at the vertices of the outermost triangle represent distributions with all disks on the same peg.
For h + 1 disks, take the graph of h disks and replace each small triangle with the graph for two disks.
For three disks the graph is:
lang=en, 400px, center


puzzle
A puzzle is a game, problem, or toy that tests a person's ingenuity or knowledge. In a puzzle, the solver is expected to put pieces together ( or take them apart) in a logical way, in order to arrive at the correct or fun solution of the puzzl ...
consisting of three rods and a number of disks of various diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle. It can also be defined as the longest chord of the circle. Both definitions are also valid f ...
s, which can slide onto any rod. The puzzle begins with the disks stacked on one rod in order of decreasing size, the smallest at the top, thus approximating a conical
A cone is a three-dimensional geometric shape that tapers smoothly from a flat base (frequently, though not necessarily, circular) to a point called the apex or vertex.
A cone is formed by a set of line segments, half-lines, or lines c ...
shape. The objective of the puzzle is to move the entire stack to the last rod, obeying the following rules:
# Only one disk may be moved at a time.
# Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack or on an empty rod.
# No disk may be placed on top of a disk that is smaller than it.
With 3 disks, the puzzle can be solved in 7 moves. The minimal number of moves required to solve a Tower of Hanoi puzzle is 2''n'' − 1, where ''n'' is the number of disks.
Origins
The puzzle was introduced to the West by theFrench
French (french: français(e), link=no) may refer to:
* Something of, from, or related to France
** French language, which originated in France, and its various dialects and accents
** French people, a nation and ethnic group identified with Franc ...
mathematician
A mathematician is someone who uses an extensive knowledge of mathematics in their work, typically to solve mathematical problems.
Mathematicians are concerned with numbers, data, quantity, structure, space, models, and change.
History
On ...
Édouard Lucas in 1883. Numerous myths regarding the ancient and mystical nature of the puzzle popped up almost immediately, including one about an India
India, officially the Republic of India (Hindi: ), is a country in South Asia. It is the List of countries and dependencies by area, seventh-largest country by area, the List of countries and dependencies by population, second-most populous ...
n temple in Kashi Vishwanath containing a large room with three time-worn posts in it, surrounded by 64 golden disks. Acting out the command of an ancient prophecy, Brahmin
Brahmin (; sa, ब्राह्मण, brāhmaṇa) is a varna as well as a caste within Hindu society. The Brahmins are designated as the priestly class as they serve as priests ( purohit, pandit, or pujari) and religious teachers ( ...
priests have been moving these disks in accordance with the immutable rules of Brahma since that time. The puzzle is therefore also known as the Tower of Brahma
Brahma ( sa, ब्रह्मा, Brahmā) is a Hindu god, referred to as "the Creator" within the Trimurti, the trinity of supreme divinity that includes Vishnu, and Shiva.Jan Gonda (1969)The Hindu Trinity Anthropos, Bd 63/64, H 1/2, pp ...
. According to the legend, when the last move of the puzzle is completed, the world will end.
If the legend were true, and if the priests were able to move disks at a rate of one per second, using the smallest number of moves, it would take them 264 − 1 seconds or roughly 585 billion
Billion is a word for a large number, and it has two distinct definitions:
*1,000,000,000, i.e. one thousand million, or (ten to the ninth power), as defined on the short scale. This is its only current meaning in English.
* 1,000,000,000,000, i. ...
years to finish, which is about 42 times the current age of the universe.
There are many variations on this legend. For instance, in some tellings, the temple is a monastery
A monastery is a building or complex of buildings comprising the domestic quarters and workplaces of monastics, monks or nuns, whether living in communities or alone (hermits). A monastery generally includes a place reserved for prayer whic ...
, and the priests are monk
A monk (, from el, μοναχός, ''monachos'', "single, solitary" via Latin ) is a person who practices religious asceticism by monastic living, either alone or with any number of other monks. A monk may be a person who decides to dedic ...
s. The temple or monastery may be in various locales including Hanoi
Hanoi or Ha Noi ( or ; vi, Hà Nội ) is the capital and second-largest city of Vietnam. It covers an area of . It consists of 12 urban districts, one district-leveled town and 17 rural districts. Located within the Red River Delta, Hanoi i ...
, and may be associated with any religion
Religion is usually defined as a social- cultural system of designated behaviors and practices, morals, beliefs, worldviews, texts, sanctified places, prophecies, ethics, or organizations, that generally relates humanity to supernatur ...
. In some versions, other elements are introduced, such as the fact that the tower was created at the beginning of the world, or that the priests or monks may make only one move per day.
Solution
The puzzle can be played with any number of disks, although many toy versions have around 7 to 9 of them. The minimal number of moves required to solve a Tower of Hanoi puzzle is , where ''n'' is the number of disks.Iterative solution
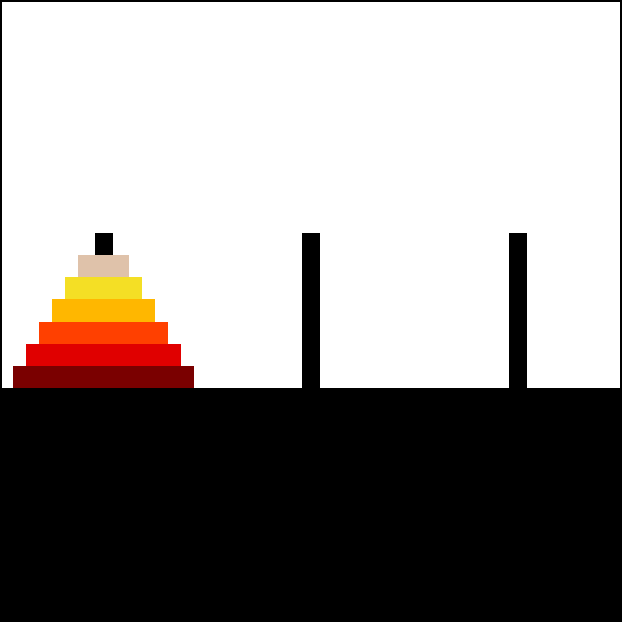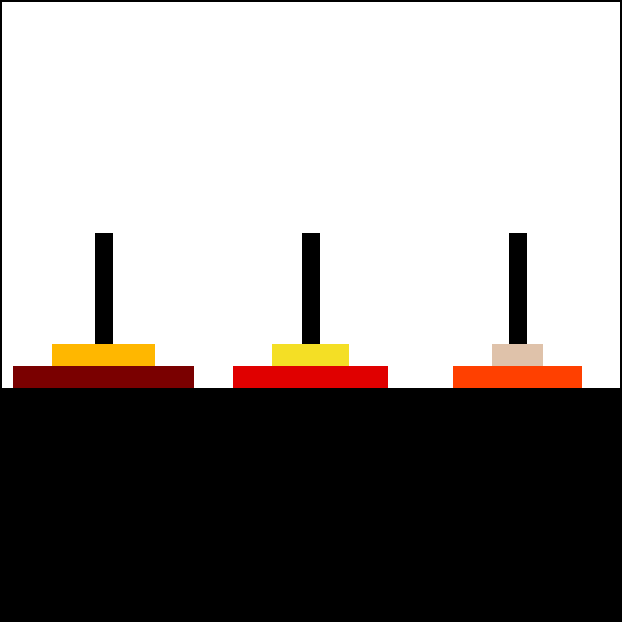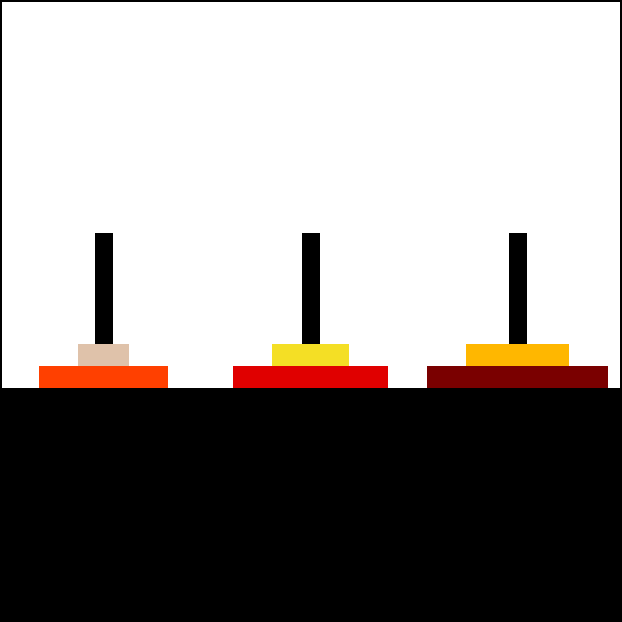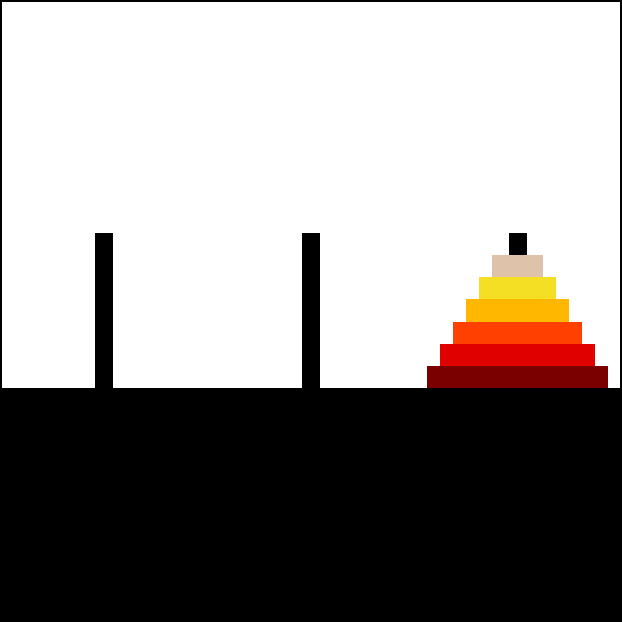 A simple solution for the toy puzzle is to alternate moves between the smallest piece and a non-smallest piece. When moving the smallest piece, always move it to the next position in the same direction (to the right if the starting number of pieces is even, to the left if the starting number of pieces is odd). If there is no tower position in the chosen direction, move the piece to the opposite end, but then continue to move in the correct direction. For example, if you started with three pieces, you would move the smallest piece to the opposite end, then continue in the left direction after that. When the turn is to move the non-smallest piece, there is only one legal move. Doing this will complete the puzzle in the fewest moves.
A simple solution for the toy puzzle is to alternate moves between the smallest piece and a non-smallest piece. When moving the smallest piece, always move it to the next position in the same direction (to the right if the starting number of pieces is even, to the left if the starting number of pieces is odd). If there is no tower position in the chosen direction, move the piece to the opposite end, but then continue to move in the correct direction. For example, if you started with three pieces, you would move the smallest piece to the opposite end, then continue in the left direction after that. When the turn is to move the non-smallest piece, there is only one legal move. Doing this will complete the puzzle in the fewest moves.
Simpler statement of iterative solution
For an even number of disks: * make the legal move between pegs A and B (in either direction), * make the legal move between pegs A and C (in either direction), * make the legal move between pegs B and C (in either direction), * repeat until complete. For an odd number of disks: * make the legal move between pegs A and C (in either direction), * make the legal move between pegs A and B (in either direction), * make the legal move between pegs B and C (in either direction), * repeat until complete. In each case, a total of 2n − 1 moves are made.Equivalent iterative solution
Another way to generate the unique optimal iterative solution: Number the disks 1 through ''n'' (largest to smallest). * If ''n'' is odd, the first move is from peg A to peg C. * If ''n'' is even, the first move is from peg A to peg B. Now, add these constraints: * No odd disk may be placed directly on an odd disk. * No even disk may be placed directly on an even disk. * There will sometimes be two possible pegs: one will have disks, and the other will be empty. Place the disk on the non-empty peg. * Never move a disk twice in succession. Considering those constraints after the first move, there is only one legal move at every subsequent turn. The sequence of these unique moves is an optimal solution to the problem equivalent to the iterative solution described above.Recursive solution
mathematical induction
Mathematical induction is a method for proving that a statement ''P''(''n'') is true for every natural number ''n'', that is, that the infinitely many cases ''P''(0), ''P''(1), ''P''(2), ''P''(3), ... all hold. Informal metaphors help ...
and is often used as an example of recursion when teaching programming.
Logical analysis of the recursive solution
As in many mathematical puzzles, finding a solution is made easier by solving a slightly more general problem: how to move a tower of ''h'' (height) disks from a starting peg ''f'' = A (from) onto a destination peg ''t'' = C (to), B being the remaining third peg and assuming ''t'' ≠ ''f''. First, observe that the problem is symmetric for permutations of the names of the pegs ( symmetric group ''S''3). If a solution is known moving from peg A to peg C, then, by renaming the pegs, the same solution can be used for every other choice of starting and destination peg. If there is only one disk (or even none at all), the problem is trivial. If ''h'' = 1, then simply move the disk from peg A to peg C. If ''h'' > 1, then somewhere along the sequence of moves, the largest disk must be moved from peg A to another peg, preferably to peg C. The only situation that allows this move is when all smaller ''h'' − 1 disks are on peg B. Hence, first all ''h'' − 1 smaller disks must go from A to B. Then move the largest disk and finally move the ''h'' − 1 smaller disks from peg B to peg C. The presence of the largest disk does not impede any move of the ''h'' − 1 smaller disks and can be temporarily ignored. Now the problem is reduced to moving ''h'' − 1 disks from one peg to another one, first from A to B and subsequently from B to C, but the same method can be used both times by renaming the pegs. The same strategy can be used to reduce the ''h'' − 1 problem to ''h'' − 2, ''h'' − 3, and so on until only one disk is left. This is called recursion. This algorithm can be schematized as follows. Identify the disks in order of increasing size by the natural numbers from 0 up to but not including ''h''. Hence disk 0 is the smallest one, and disk ''h'' − 1 the largest one. The following is a procedure for moving a tower of ''h'' disks from a peg A onto a peg C, with B being the remaining third peg: # If ''h'' > 1, then first use this procedure to move the ''h'' − 1 smaller disks from peg A to peg B. # Now the largest disk, i.e. disk ''h'' can be moved from peg A to peg C. # If ''h'' > 1, then again use this procedure to move the ''h'' − 1 smaller disks from peg B to peg C. By means ofmathematical induction
Mathematical induction is a method for proving that a statement ''P''(''n'') is true for every natural number ''n'', that is, that the infinitely many cases ''P''(0), ''P''(1), ''P''(2), ''P''(3), ... all hold. Informal metaphors help ...
, it is easily proven that the above procedure requires the minimal number of moves possible and that the produced solution is the only one with this minimal number of moves. Using recurrence relation
In mathematics, a recurrence relation is an equation according to which the nth term of a sequence of numbers is equal to some combination of the previous terms. Often, only k previous terms of the sequence appear in the equation, for a parameter ...
s, the exact number of moves that this solution requires can be calculated by: . This result is obtained by noting that steps 1 and 3 take moves, and step 2 takes one move, giving .
Recursive implementation
The following Python code demonstrates the recursive solution., 2, 1
The comma is a punctuation mark that appears in several variants in different languages. It has the same shape as an apostrophe or single closing quotation mark () in many typefaces, but it differs from them in being placed on the baseline o ...
B = []
C = []
def move(n, source, target, auxiliary):
if n > 0:
# Move n - 1 disks from source to auxiliary, so they are out of the way
move(n - 1, source, auxiliary, target)
# Move the nth disk from source to target
target.append(source.pop())
# Display our progress
print(A, B, C, '##############', sep='\n')
# Move the n - 1 disks that we left on auxiliary onto target
move(n - 1, auxiliary, target, source)
# Initiate call from source A to target C with auxiliary B
move(3, A, C, B)
Non-recursive solution
The list of moves for a tower being carried from one peg onto another one, as produced by the recursive algorithm, has many regularities. When counting the moves starting from 1, the ordinal of the disk to be moved during move ''m'' is the number of times ''m'' can be divided by 2. Hence every odd move involves the smallest disk. It can also be observed that the smallest disk traverses the pegs ''f'', ''t'', ''r'', ''f'', ''t'', ''r'', etc. for odd height of the tower and traverses the pegs ''f'', ''r'', ''t'', ''f'', ''r'', ''t'', etc. for even height of the tower. This provides the following algorithm, which is easier, carried out by hand, than the recursive algorithm. In alternate moves: * Move the smallest disk to the peg it has not recently come from. * Move another disk legally (there will be only one possibility). For the very first move, the smallest disk goes to peg ''t'' if ''h'' is odd and to peg ''r'' if ''h'' is even. Also observe that: * Disks whose ordinals have even parity move in the same sense as the smallest disk. * Disks whose ordinals have odd parity move in opposite sense. * If ''h'' is even, the remaining third peg during successive moves is ''t'', ''r'', ''f'', ''t'', ''r'', ''f'', etc. * If ''h'' is odd, the remaining third peg during successive moves is ''r'', ''t'', ''f'', ''r'', ''t'', ''f'', etc. With this knowledge, a set of disks in the middle of an optimal solution can be recovered with no more state information than the positions of each disk: * Call the moves detailed above a disk's "natural" move. * Examine the smallest top disk that is not disk 0, and note what its only (legal) move would be: if there is no such disk, then we are either at the first or last move. * If that move is the disk's "natural" move, then the disk has not been moved since the last disk 0 move, and that move should be taken. * If that move is not the disk's "natural" move, then move disk 0.Binary solution
Disk positions may be determined more directly from the binary (base-2) representation of the move number (the initial state being move #0, with all digits 0, and the final state being with all digits 1), using the following rules: * There is one binary digit ( bit) for each disk. * The most significant (leftmost) bit represents the largest disk. A value of 0 indicates that the largest disk is on the initial peg, while a 1 indicates that it's on the final peg (right peg if number of disks is odd and middle peg otherwise). * The bitstring is read from left to right, and each bit can be used to determine the location of the corresponding disk. * A bit with the same value as the previous one means that the corresponding disk is stacked on top of the previous disk on the same peg. *: (That is to say: a straight sequence of 1s or 0s means that the corresponding disks are all on the same peg.) * A bit with a different value to the previous one means that the corresponding disk is one position to the left or right of the previous one. Whether it is left or right is determined by this rule: ** Assume that the initial peg is on the left. ** Also assume "wrapping" – so the right peg counts as one peg "left" of the left peg, and vice versa. ** Let ''n'' be the number of greater disks that are located on the same peg as their first greater disk and add 1 if the largest disk is on the left peg. If ''n'' is even, the disk is located one peg to the right, if ''n'' is odd, the disk located one peg to the left (in case of even number of disks and vice versa otherwise). For example, in an 8-disk Hanoi: * Move 0 = 00000000. ** The largest disk is 0, so it is on the left (initial) peg. ** All other disks are 0 as well, so they are stacked on top of it. Hence all disks are on the initial peg. * Move 28 − 1 = 11111111. ** The largest disk is 1, so it is on the middle (final) peg. ** All other disks are 1 as well, so they are stacked on top of it. Hence all disks are on the final peg and the puzzle is complete. * Move 21610 = 11011000. ** The largest disk is 1, so it is on the middle (final) peg. ** Disk two is also 1, so it is stacked on top of it, on the middle peg. ** Disk three is 0, so it is on another peg. Since ''n'' is odd (''n'' = 1), it is one peg to the left, i.e. on the left peg. ** Disk four is 1, so it is on another peg. Since ''n'' is odd (''n'' = 1), it is one peg to the left, i.e. on the right peg. ** Disk five is also 1, so it is stacked on top of it, on the right peg. ** Disk six is 0, so it is on another peg. Since ''n'' is even (''n'' = 2), the disk is one peg to the right, i.e. on the left peg. ** Disks seven and eight are also 0, so they are stacked on top of it, on the left peg. The source and destination pegs for the ''m''th move can also be found elegantly from the binary representation of ''m'' usingbitwise operation
In computer programming, a bitwise operation operates on a bit string, a bit array or a binary numeral (considered as a bit string) at the level of its individual bits. It is a fast and simple action, basic to the higher-level arithmetic oper ...
s. To use the syntax of the C programming language
''The C Programming Language'' (sometimes termed ''K&R'', after its authors' initials) is a computer programming book written by Brian Kernighan and Dennis Ritchie, the latter of whom originally designed and implemented the language, as well a ...
, move ''m'' is from peg (m & m - 1) % 3 to peg ((m , m - 1) + 1) % 3, where the disks begin on peg 0 and finish on peg 1 or 2 according as whether the number of disks is even or odd. Another formulation is from peg (m - (m & -m)) % 3 to peg (m + (m & -m)) % 3.
Furthermore, the disk to be moved is determined by the number of times the move count (''m'') can be divided by 2 (i.e. the number of zero bits at the right), counting the first move as 1 and identifying the disks by the numbers 0, 1, 2, etc. in order of increasing size. This permits a very fast non-recursive computer implementation to find the positions of the disks after m moves without reference to any previous move or distribution of disks.
The operation, which counts the number of consecutive zeros at the end of a binary number, gives a simple solution to the problem: the disks are numbered from zero, and at move ''m'', disk number count trailing zeros is moved the minimal possible distance to the right (circling back around to the left as needed).
Gray-code solution
The binary numeral system ofGray code
The reflected binary code (RBC), also known as reflected binary (RB) or Gray code after Frank Gray, is an ordering of the binary numeral system such that two successive values differ in only one bit (binary digit).
For example, the representa ...
s gives an alternative way of solving the puzzle. In the Gray system, numbers are expressed in a binary combination of 0s and 1s, but rather than being a standard positional numeral system
Positional notation (or place-value notation, or positional numeral system) usually denotes the extension to any base of the Hindu–Arabic numeral system (or decimal system). More generally, a positional system is a numeral system in which th ...
, the Gray code operates on the premise that each value differs from its predecessor by only one (and exactly one) bit changed.
If one counts in Gray code of a bit size equal to the number of disks in a particular Tower of Hanoi, begins at zero and counts up, then the bit changed each move corresponds to the disk to move, where the least-significant bit is the smallest disk, and the most-significant bit is the largest.
:Counting moves from 1 and identifying the disks by numbers starting from 0 in order of increasing size, the ordinal of the disk to be moved during move ''m'' is the number of times ''m'' can be divided by 2.
This technique identifies which disk to move, but not where to move it to. For the smallest disk, there are always two possibilities. For the other disks there is always one possibility, except when all disks are on the same peg, but in that case either it is the smallest disk that must be moved or the objective has already been achieved. Luckily, there is a rule that does say where to move the smallest disk to. Let ''f'' be the starting peg, ''t'' the destination peg, and ''r'' the remaining third peg. If the number of disks is odd, the smallest disk cycles along the pegs in the order ''f'' → ''t'' → ''r'' → ''f'' → ''t'' → ''r'', etc. If the number of disks is even, this must be reversed: ''f'' → ''r'' → ''t'' → ''f'' → ''r'' → ''t'', etc.
The position of the bit change in the Gray code solution gives the size of the disk moved at each step: 1, 2, 1, 3, 1, 2, 1, 4, 1, 2, 1, 3, 1, 2, 1, ... , a sequence also known as the ruler function
In number theory, the ruler function of an integer n can be either of two closely-related functions. One of these functions counts the number of times n can be evenly divided by two, which for the numbers 1, 2, 3, ... is
Alternatively, the ruler f ...
, or one more than the power of 2 within the move number. In the Wolfram Language
The Wolfram Language ( ) is a general multi-paradigm programming language developed by Wolfram Research. It emphasizes symbolic computation, functional programming, and rule-based programming and can employ arbitrary structures and data. It ...
, IntegerExponent ange[2^8_-_1_2.html"_;"title="^8_-_1.html"_;"title="ange[2^8_-_1">ange[2^8_-_1_2">^8_-_1.html"_;"title="ange[2^8_-_1">ange[2^8_-_1_2+_1_gives_moves_for_the_8-disk_puzzle.
__Graphical_representation_
The_game_can_be_represented_by_an_ ange[2^8_-_1_2.html"_;"title="^8_-_1.html"_;"title="ange[2^8_-_1">ange[2^8_-_1_2">^8_-_1.html"_;"title="ange[2^8_-_1">ange[2^8_-_1_2+_1_gives_moves_for_the_8-disk_puzzle.__Graphical_representation_
The_game_can_be_represented_by_an_Graph_(discrete_mathematics)#Undirected_graph">undirected_graphGraphical representation
The game can be represented by an Graph (discrete mathematics)#Undirected graph">undirected graph In discrete mathematics, and more specifically in graph theory, a graph is a structure amounting to a set of objects in which some pairs of the objects are in some sense "related". The objects correspond to mathematical abstractions called '' ve ...fractal
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as ill ...
figure, the Sierpiński triangle. It is clear that the great majority of positions in the puzzle will never be reached when using the shortest possible solution; indeed, if the priests of the legend are using the longest possible solution (without re-visiting any position), it will take them 364 − 1 moves, or more than 1023 years.
The longest non-repetitive way for three disks can be visualized by erasing the unused edges:
lang=pa, 400px, center
Incidentally, this longest non-repetitive path can be obtained by forbidding all moves from ''a'' to ''c''.
The Hamiltonian cycle
In the mathematical field of graph theory, a Hamiltonian path (or traceable path) is a path in an undirected or directed graph that visits each vertex exactly once. A Hamiltonian cycle (or Hamiltonian circuit) is a cycle that visits each vertex ...
for three disks is:
lang=cy, 400px, center
The graphs clearly show that:
* From every arbitrary distribution of disks, there is exactly one shortest way to move all disks onto one of the three pegs.
* Between every pair of arbitrary distributions of disks there are one or two different shortest paths.
* From every arbitrary distribution of disks, there are one or two different longest non selfcrossing paths to move all disks to one of the three pegs.
* Between every pair of arbitrary distributions of disks there are one or two different longest non self-crossing paths.
* Let ''N''''h'' be the number of non-self-crossing paths for moving a tower of ''h'' disks from one peg to another one. Then:
** ''N''1 = 2
** ''N''''h''+1 = (''N''''h'')2 + (''N''''h'')3
This gives ''N''''h'' to be 2, 12, 1872, 6563711232, ...
Variations
Adjacent pegs
If all moves must be between adjacent pegs (i.e. given pegs A, B, C, one cannot move directly between pegs A and C), then moving a stack of ''n'' disks from peg A to peg C takes 3''n'' − 1 moves. The solution uses all 3n valid positions, always taking the unique move that does not undo the previous move. The position with all disks at peg B is reached halfway, i.e. after (3''n'' − 1) / 2 moves.Cyclic Hanoi
In Cyclic Hanoi, we are given three pegs (A, B, C), which are arranged as a circle with the clockwise and the counterclockwise directions being defined as A – B – C – A and A – C – B – A respectively. The moving direction of the disk must be clockwise. It suffices to represent the sequence of disks to be moved. The solution can be found using two mutually recursive procedures: To move ''n'' disks counterclockwise to the neighbouring target peg: # move ''n'' − 1 disks counterclockwise to the target peg # move disk #''n'' one step clockwise # move ''n'' − 1 disks clockwise to the start peg # move disk #''n'' one step clockwise # move ''n'' − 1 disks counterclockwise to the target peg To move ''n'' disks clockwise to the neighbouring target peg: # move ''n'' − 1 disks counterclockwise to a spare peg # move disk #''n'' one step clockwise # move ''n'' − 1 disks counterclockwise to the target peg Let C(n) and A(n) represent moving n disks clockwise and counterclockwise, then we can write down both formulas: C(n) = A(n-1) n A(n-1) and A(n) = A(n-1) n C(n-1) n A(n-1). Thus C(1) = 1 and A(1) = 1 1, C(2) = 1 1 2 1 1 and A(2) = 1 1 2 1 2 1 1. The solution for the Cyclic Hanoi has some interesting properties: 1)The move-patterns of transferring a tower of disks from a peg to another peg are symmetric with respect to the center points. 2)The smallest disk is the first and last disk to move. 3)Groups of the smallest disk moves alternate with single moves of other disks. 4)The number of disks moves specified by C(n) and A(n) are minimal.With four pegs and beyond
Although the three-peg version has a simple recursive solution long been known, the optimal solution for the Tower of Hanoi problem with four pegs (called Reve's puzzle) was not verified until 2014, by Bousch. However, in case of four or more pegs, the Frame–Stewart algorithm is known without proof of optimality since 1941. For the formal derivation of the exact number of minimal moves required to solve the problem by applying the Frame–Stewart algorithm (and other equivalent methods), see the following paper. For other variants of the four-peg Tower of Hanoi problem, see Paul Stockmeyer's survey paper. The so-called Towers of Bucharest and Towers of Klagenfurt game configurations yield ternary and pentary Gray codes.Frame–Stewart algorithm
The Frame–Stewart algorithm is described below: * Let be the number of disks. * Let be the number of pegs. * Define to be the minimum number of moves required to transfer n disks using r pegs. The algorithm can be described recursively: # For some , , transfer the top disks to a single peg other than the start or destination pegs, taking moves. # Without disturbing the peg that now contains the top disks, transfer the remaining disks to the destination peg, using only the remaining pegs, taking moves. # Finally, transfer the top disks to the destination peg, taking moves. The entire process takes moves. Therefore, the count should be picked for which this quantity is minimum. In the 4-peg case, the optimal equals , where is thenearest integer function
Rounding means replacing a number with an approximate value that has a shorter, simpler, or more explicit representation. For example, replacing $ with $, the fraction 312/937 with 1/3, or the expression with .
Rounding is often done to obt ...
. For example, in the UPenn CIS 194 course on Haskell, the first assignment page lists the optimal solution for the 15-disk and 4-peg case as 129 steps, which is obtained for the above value of ''k''.
This algorithm is presumed to be optimal for any number of pegs; its number of moves is 2 Θ(''n''1/(''r''−2)) (for fixed ''r'').
General shortest paths and the number 466/885
A curious generalization of the original goal of the puzzle is to start from a given configuration of the disks where all disks are not necessarily on the same peg and to arrive in a minimal number of moves at another given configuration. In general, it can be quite difficult to compute a shortest sequence of moves to solve this problem. A solution was proposed by Andreas Hinz and is based on the observation that in a shortest sequence of moves, the largest disk that needs to be moved (obviously one may ignore all of the largest disks that will occupy the same peg in both the initial and final configurations) will move either exactly once or exactly twice. The mathematics related to this generalized problem becomes even more interesting when one considers the ''average'' number of moves in a shortest sequence of moves between two initial and final disk configurations that are chosen at random. Hinz and Chan Tat-Hung independently discovered (see also ) that the average number of moves in an n-disk Tower is given by the following exact formula: : For large enough ''n'', only the first and second terms do not converge to zero, so we get an asymptotic expression: , as . Thus intuitively, we could interpret the fraction of as representing the ratio of the labor one has to perform when going from a randomly chosen configuration to another randomly chosen configuration, relative to the difficulty of having to cross the "most difficult" path of length which involves moving all the disks from one peg to another. An alternative explanation for the appearance of the constant 466/885, as well as a new and somewhat improved algorithm for computing the shortest path, was given by Romik.Magnetic Hanoi
In Magnetic Tower of Hanoi, each disk has two distinct sides North and South (typically colored "red" and "blue"). Disks must not be placed with the similar poles together—magnets in each disk prevent this illegal move. Also, each disk must be flipped as it is moved.
Bicolor Towers of Hanoi
This variation of the famous Tower of Hanoi puzzle was offered to grade 3–6 students at ''2ème Championnat de France des Jeux Mathématiques et Logiques'' held in July 1988. The rules of the puzzle are essentially the same: disks are transferred between pegs one at a time. At no time may a bigger disk be placed on top of a smaller one. The difference is that now for every size there are two disks: one black and one white. Also, there are now two towers of disks of alternating colors. The goal of the puzzle is to make the towers monochrome (same color). The biggest disks at the bottom of the towers are assumed to swap positions.
The rules of the puzzle are essentially the same: disks are transferred between pegs one at a time. At no time may a bigger disk be placed on top of a smaller one. The difference is that now for every size there are two disks: one black and one white. Also, there are now two towers of disks of alternating colors. The goal of the puzzle is to make the towers monochrome (same color). The biggest disks at the bottom of the towers are assumed to swap positions.
Tower of Hanoy
A variation of the puzzle has been adapted as a solitaire game with nine playing cards under the nameTower of Hanoy
Tower of Hanoy is a solitaire card game which only uses 9 playing cards. It is based on the actual Tower of Hanoi game, where the object is to transfer discs from one peg to another without disturbing their order. The origin of the spelling is unc ...
. It is not known whether the altered spelling of the original name is deliberate or accidental.
Applications
problem-solving
Problem solving is the process of achieving a goal by overcoming obstacles, a frequent part of most activities. Problems in need of solutions range from simple personal tasks (e.g. how to turn on an appliance) to complex issues in business an ...
. There also exists a variant of this task called Tower of London
The Tower of London, officially His Majesty's Royal Palace and Fortress of the Tower of London, is a historic castle on the north bank of the River Thames in central London. It lies within the London Borough of Tower Hamlets, which is sep ...
for neuropsychological diagnosis and treatment of executive functions.
Zhang and Norman used several isomorphic (equivalent) representations of the game to study the impact of representational effect in task design. They demonstrated an impact on user performance by changing the way that the rules of the game are represented, using variations in the physical design of the game components. This knowledge has impacted on the development of the TURF framework for the representation of human–computer interaction
Human–computer interaction (HCI) is research in the design and the use of computer technology, which focuses on the interfaces between people (users) and computers. HCI researchers observe the ways humans interact with computers and design te ...
.
The Tower of Hanoi is also used as a backup rotation scheme
A backup rotation scheme is a system of backing up data to computer media (such as tapes) that minimizes, by re-use, the number of media used. The scheme determines how and when each piece of removable storage is used for a backup job and how lo ...
when performing computer data backups
In information technology, a backup, or data backup is a copy of computer data taken and stored elsewhere so that it may be used to restore the original after a data loss event. The verb form, referring to the process of doing so, is "back up", ...
where multiple tapes/media are involved.
As mentioned above, the Tower of Hanoi is popular for teaching recursive algorithms to beginning programming students. A pictorial version of this puzzle is programmed into the emacs
Emacs , originally named EMACS (an acronym for "Editor MACroS"), is a family of text editors that are characterized by their extensibility. The manual for the most widely used variant, GNU Emacs, describes it as "the extensible, customizable, ...
editor, accessed by typing M-x hanoi. There is also a sample algorithm written in Prolog
Prolog is a logic programming language associated with artificial intelligence and computational linguistics.
Prolog has its roots in first-order logic, a formal logic, and unlike many other programming languages, Prolog is intended primarily ...
.
The Tower of Hanoi is also used as a test by neuropsychologists trying to evaluate frontal lobe
The frontal lobe is the largest of the four major lobes of the brain in mammals, and is located at the front of each cerebral hemisphere (in front of the parietal lobe and the temporal lobe). It is parted from the parietal lobe by a groove be ...
deficits.
In 2010, researchers published the results of an experiment that found that the ant species ''Linepithema humile
The Argentine ant (''Linepithema humile''), formerly ''Iridomyrmex humilis'', is an ant native to northern Argentina, Uruguay, Paraguay, Bolivia and southern Brazil. It is an invasive species that has been established in many Mediterranean clima ...
'' were successfully able to solve the 3-disk version of the Tower of Hanoi problem through non-linear dynamics and pheromone signals.
In 2014, scientists synthesized multilayered palladium nanosheets with a Tower of Hanoi like structure.
In popular culture
In the science fiction story "Now Inhale", by Eric Frank Russell, a human is held prisoner on a planet where the local custom is to make the prisoner play a game until it is won or lost before his execution. The protagonist knows that a rescue ship might take a year or more to arrive, so he chooses to play Towers of Hanoi with 64 disks. This story makes reference to the legend about the Buddhist monks playing the game until the end of the world. In the 1966 ''Doctor Who
''Doctor Who'' is a British science fiction television series broadcast by the BBC since 1963. The series depicts the adventures of a Time Lord called the Doctor, an extraterrestrial being who appears to be human. The Doctor explores the ...
'' story ''The Celestial Toymaker
''The Celestial Toymaker'' is the mostly missing sixth serial of the third season in the British science fiction television programme ''Doctor Who'', which was first broadcast in four weekly parts from 2 to 23 April 1966.
In this serial, th ...
'', the eponym
An eponym is a person, a place, or a thing after whom or which someone or something is, or is believed to be, named. The adjectives which are derived from the word eponym include ''eponymous'' and ''eponymic''.
Usage of the word
The term ''epon ...
ous villain forces the Doctor to play a ten-piece 1,023-move Tower of Hanoi game entitled The Trilogic Game with the pieces forming a pyramid shape when stacked.
In 2007, the concept of the Towers Of Hanoi problem was used in '' Professor Layton and the Diabolical Box'' in puzzles 6, 83, and 84, but the disks had been changed to pancakes. The puzzle was based around a dilemma where the chef of a restaurant had to move a pile of pancakes from one plate to the other with the basic principles of the original puzzle (i.e. three plates that the pancakes could be moved onto, not being able to put a larger pancake onto a smaller one, etc.)
In the film '' Rise of the Planet of the Apes'' (2011), this puzzle, called in the film the "Lucas Tower", is used as a test to study the intelligence of apes.
The puzzle is featured regularly in adventure
An adventure is an exciting experience or undertaking that is typically bold, sometimes risky. Adventures may be activities with danger such as traveling, exploring, skydiving, mountain climbing, scuba diving, river rafting, or other extreme ...
and puzzle
A puzzle is a game, problem, or toy that tests a person's ingenuity or knowledge. In a puzzle, the solver is expected to put pieces together ( or take them apart) in a logical way, in order to arrive at the correct or fun solution of the puzzl ...
games. Since it is easy to implement, and easily recognised, it is well-suited to use as a puzzle in a larger graphical game (e.g. '' Star Wars: Knights of the Old Republic'' and ''Mass Effect
''Mass Effect'' is a military science fiction media franchise created by Casey Hudson, Drew Karpyshyn and Preston Watamaniuk. The franchise depicts a distant future where humanity and several alien civilizations have colonized the known unive ...
''). Some implementations use straight disks, but others disguise the puzzle in some other form. There is an arcade version by Sega
is a Japanese multinational video game and entertainment company headquartered in Shinagawa, Tokyo. Its international branches, Sega of America and Sega Europe, are headquartered in Irvine, California and London, respectively. Its division ...
.
A 15-disk version of the puzzle appears in the game '' Sunless Sea'' as a lock to a tomb. The player has the option to click through each move of the puzzle in order to solve it, but the game notes that it will take 32767 moves to complete. If an especially dedicated player does click through to the end of the puzzle, it is revealed that completing the puzzle does not unlock the door.
In ''Yu-Gi-Oh! VRAINS
is a Japanese anime series animated by Gallop. It is the sixth main anime series in the ''Yu-Gi-Oh!'' franchise. The series aired in Japan on TV Tokyo from May 10, 2017 to September 25, 2019. It was simulcast outside of Asia by Crunchyroll ...
'', a hacking group called "Knight of Hanoi" create a structure named "Tower of Hanoi" within the eponymous VRAINS virtual reality network.
This was first used as a challenge in ''Survivor'' Thailand in 2002 but rather than rings, the pieces were made to resemble a temple. Sook Jai threw the challenge to get rid of Jed even though Shii-Ann knew full well how to complete the puzzle.
The problem is featured as part of a reward challenge in a 2011 episode of the American version of the ''Survivor'' TV series. Both players (Ozzy Lusth
Ozcar "Ozzy" Lusth (born August 23, 1981) is a Mexican-born American reality show veteran contestant who has appeared on several shows, including '' Survivor: Cook Islands''; '' Survivor: Micronesia;'' and '' Survivor: South Pacific''. He also com ...
and Benjamin "Coach" Wade
Benjamin "Coach" Wade (born September 18, 1971) is an American reality television personality best known for being a contestant on '' Survivor: Tocantins'', '' Survivor: Heroes vs. Villains'', and '' Survivor: South Pacific''. He grew up in Kno ...
) struggled to understand how to solve the puzzle and are aided by their fellow tribe members.
See also
*ABACABA pattern
The ABACABA pattern is a recursive fractal pattern that shows up in many places in the real world (such as in geometry, art, music, poetry, number systems, literature and higher dimensions). Patterns often show a DABACABA type subset. ''AA'', ' ...
* Backup rotation scheme
A backup rotation scheme is a system of backing up data to computer media (such as tapes) that minimizes, by re-use, the number of media used. The scheme determines how and when each piece of removable storage is used for a backup job and how lo ...
, a TOH application
* Baguenaudier
Baguenaudier (; French for "time-waster"), also known as the Chinese rings, Cardan's suspension, Cardano's rings, Devil's needle or five pillars puzzle, is a disentanglement puzzle featuring a loop which must be disentangled from a sequence of ...
* Recursion (computer science)
In computer science, recursion is a method of solving a computational problem where the solution depends on solutions to smaller instances of the same problem. Recursion solves such recursive problems by using functions that call themselves ...
Notes
External links
* {{mathworld, title=Tower of Hanoi, urlname=TowerofHanoi Mechanical puzzles Mathematical puzzles Articles with example Python (programming language) code