Theorems In The Foundations Of Mathematics

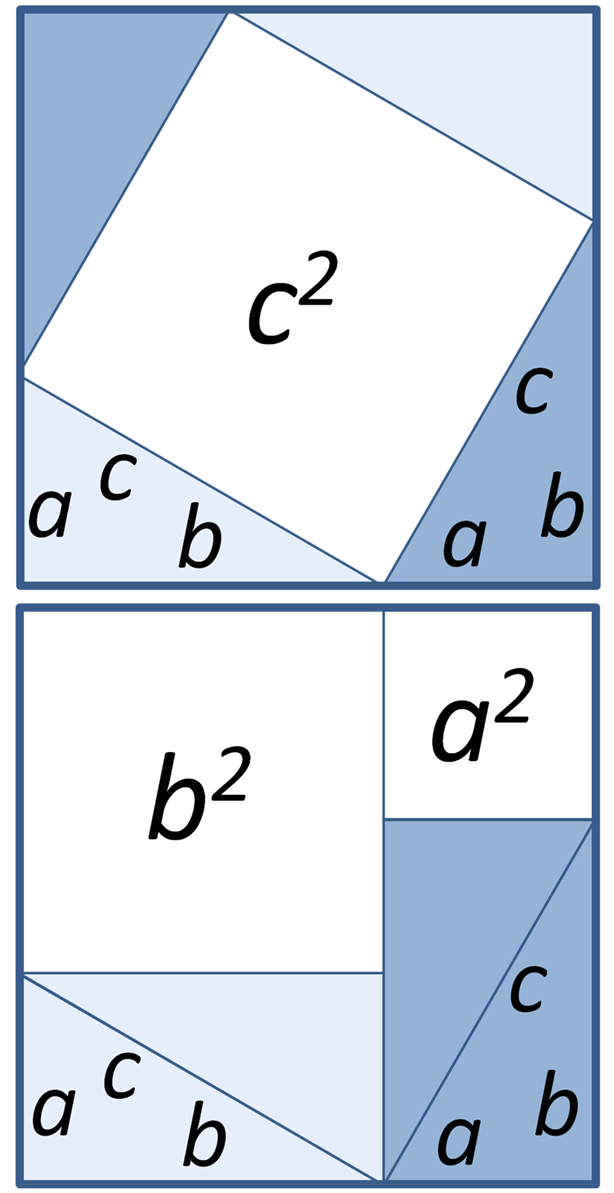In mathematics, a theorem is a statement that has been proved, or can be proved. The ''proof'' of a theorem is a logical argument that uses the inference rules of a deductive system to establish that the theorem is a logical consequence of the axioms and previously proved theorems.

In the mainstream of mathematics, the axioms and the inference rules are commonly left implicit, and, in this case, they are almost always those of Zermelo–Fraenkel set theory with the axiom of choice, or of a less powerful theory, such as Peano arithmetic. A notable exception is Wiles's proof of Fermat's Last Theorem, which involves the Grothendieck universes whose existence requires the addition of a new axiom to the set theory. Generally, an assertion that is explicitly called a theorem is a proved result that is not an immediate consequence of other known theorems. Moreover, many authors qualify as ''theorems'' only the most important results, and use the terms ''lemma'', ''proposition'' and ''corollary'' for less important theorems.

In mathematical logic, the concepts of theorems and proofs have been formalized in order to allow mathematical reasoning about them. In this context, statements become well-formed formulas of some formal language. A theory consists of some basis statements called ''axioms'', and some ''deducing rules'' (sometimes included in the axioms). The theorems of the theory are the statements that can be derived from the axioms by using the deducing rules. This formalization led to proof theory, which allows proving general theorems about theorems and proofs. In particular, Gödel's incompleteness theorems show that every consistent theory containing the natural numbers has true statements on natural numbers that are not theorems of the theory (that is they cannot be proved inside the theory).

As the axioms are often abstractions of properties of the physical world, theorems may be considered as expressing some truth, but in contrast to the notion of a scientific law, which is '' experimental'', the justification of the truth of a theorem is purely deductive.

Theoremhood and truth

Until the end of the 19th century and the foundational crisis of mathematics, all mathematical theories were built from a few basic properties that were considered as self-evident; for example, the facts that every natural number has a successor, and that there is exactly one line that passes through two given distinct points. These basic properties that were considered as absolutely evident were called postulates or axioms; for example Euclid's postulates. All theorems were proved by using implicitly or explicitly these basic properties, and, because of the evidence of these basic properties, a proved theorem was considered as a definitive truth, unless there was an error in the proof. For example, the sum of the interior angles of a triangle equals 180°, and this was considered as an undoubtful fact.

One aspect of the foundational crisis of mathematics was the discovery of non-Euclidean geometries that do not lead to any contradiction, although, in such geometries, the sum of the angles of a triangle is different from 180°. So, the property ''"the sum of the angles of a triangle equals 180°"'' is either true or false, depending whether Euclid's fifth postulate is assumed or denied. Similarly, the use of "evident" basic properties of sets leads to the contradiction of Russel's paradox. This has been resolved by elaborating the rules that are allowed for manipulating sets.

This crisis has been resolved by revisiting the foundations of mathematics to make them more rigorous. In these new foundations, a theorem is a well-formed formula of a mathematical theory that can be proved from the axioms and inference rules of the theory. So, the above theorem on the sum of the angles of a triangle becomes: ''Under the axioms and inference rules of Euclidean geometry, the sum of the interior angles of a triangle equals 180°''. Similarly, Russel's paradox disappears because, in an axiomatized set theory, the ''set of all sets'' cannot be expressed with a well-formed formula. More precisely, if the set of all sets can be expressed with a well-formed formula, this implies that the theory is inconsistent, and every well-formed assertion, as well as its negation, is a theorem.

In this context, the validity of a theorem depends only on the correctness of its proof. It is independent from the truth, or even the significance of the axioms. This does not mean that the significance of the axioms is uninteresting, but only that the validity of a theorem is independent from the significance of the axioms. This independence may be useful by allowing the use of results of some area of mathematics in apparently unrelated areas.

An important consequence of this way of thinking about mathematics is that it allows defining mathematical theories and theorems as mathematical objects, and to prove theorems about them. Examples are Gödel's incompleteness theorems. In particular, there are well-formed assertions than can be proved to not be a theorem of the ambient theory, although they can be proved in a wider theory. An example is Goodstein's theorem, which can be stated in Peano arithmetic, but is proved to be not provable in Peano arithmetic. However, it is provable in some more general theories, such as Zermelo–Fraenkel set theory.

Epistemological considerations

Many mathematical theorems are conditional statements, whose proofs deduce conclusions from conditions known as hypotheses or premises. In light of the interpretation of proof as justification of truth, the conclusion is often viewed as a necessary consequence of the hypotheses. Namely, that the conclusion is true in case the hypotheses are true—without any further assumptions. However, the conditional could also be interpreted differently in certain deductive systems, depending on the meanings assigned to the derivation rules and the conditional symbol (e.g., non-classical logic).

Although theorems can be written in a completely symbolic form (e.g., as propositions in propositional calculus), they are often expressed informally in a natural language such as English for better readability. The same is true of proofs, which are often expressed as logically organized and clearly worded informal arguments, intended to convince readers of the truth of the statement of the theorem beyond any doubt, and from which a formal symbolic proof can in principle be constructed.

In addition to the better readability, informal arguments are typically easier to check than purely symbolic ones—indeed, many mathematicians would express a preference for a proof that not only demonstrates the validity of a theorem, but also explains in some way ''why'' it is obviously true. In some cases, one might even be able to substantiate a theorem by using a picture as its proof.

Because theorems lie at the core of mathematics, they are also central to its aesthetics. Theorems are often described as being "trivial", or "difficult", or "deep", or even "beautiful". These subjective judgments vary not only from person to person, but also with time and culture: for example, as a proof is obtained, simplified or better understood, a theorem that was once difficult may become trivial. On the other hand, a deep theorem may be stated simply, but its proof may involve surprising and subtle connections between disparate areas of mathematics. Fermat's Last Theorem is a particularly well-known example of such a theorem.

Informal account of theorems

Logically, many theorems are of the form of an indicative conditional: ''If A, then B''. Such a theorem does not assert ''B'' — only that ''B'' is a necessary consequence of ''A''. In this case, ''A'' is called the ''hypothesis'' of the theorem ("hypothesis" here means something very different from a conjecture), and ''B'' the ''conclusion'' of the theorem. The two together (without the proof) are called the ''proposition'' or ''statement'' of the theorem (e.g. "''If A, then B''" is the ''proposition''). Alternatively, ''A'' and ''B'' can be also termed the '' antecedent'' and the ''consequent'', respectively. The theorem "If ''n'' is an even natural number, then ''n''/2 is a natural number" is a typical example in which the hypothesis is "''n'' is an even natural number", and the conclusion is "''n''/2 is also a natural number".

In order for a theorem be proved, it must be in principle expressible as a precise, formal statement. However, theorems are usually expressed in natural language rather than in a completely symbolic form—with the presumption that a formal statement can be derived from the informal one.

It is common in mathematics to choose a number of hypotheses within a given language and declare that the theory consists of all statements provable from these hypotheses. These hypotheses form the foundational basis of the theory and are called axioms or postulates. The field of mathematics known as proof theory studies formal languages, axioms and the structure of proofs.

Some theorems are "trivial", in the sense that they follow from definitions, axioms, and other theorems in obvious ways and do not contain any surprising insights. Some, on the other hand, may be called "deep", because their proofs may be long and difficult, involve areas of mathematics superficially distinct from the statement of the theorem itself, or show surprising connections between disparate areas of mathematics. A theorem might be simple to state and yet be deep. An excellent example is Fermat's Last Theorem, and there are many other examples of simple yet deep theorems in number theory and combinatorics, among other areas.

Other theorems have a known proof that cannot easily be written down. The most prominent examples are the four color theorem and the Kepler conjecture. Both of these theorems are only known to be true by reducing them to a computational search that is then verified by a computer program. Initially, many mathematicians did not accept this form of proof, but it has become more widely accepted. The mathematician Doron Zeilberger has even gone so far as to claim that these are possibly the only nontrivial results that mathematicians have ever proved. Many mathematical theorems can be reduced to more straightforward computation, including polynomial identities, trigonometric identities and hypergeometric identities.

Relation with scientific theories

Theorems in mathematics and theories in science are fundamentally different in their epistemology. A scientific theory cannot be proved; its key attribute is that it is falsifiable, that is, it makes predictions about the natural world that are testable by experiments. Any disagreement between prediction and experiment demonstrates the incorrectness of the scientific theory, or at least limits its accuracy or domain of validity. Mathematical theorems, on the other hand, are purely abstract formal statements: the proof of a theorem cannot involve experiments or other empirical evidence in the same way such evidence is used to support scientific theories.

Nonetheless, there is some degree of empiricism and data collection involved in the discovery of mathematical theorems. By establishing a pattern, sometimes with the use of a powerful computer, mathematicians may have an idea of what to prove, and in some cases even a plan for how to set about doing the proof. It is also possible to find a single counter-example and so establish the impossibility of a proof for the proposition as-stated, and possibly suggest restricted forms of the original proposition that might have feasible proofs.

For example, both the Collatz conjecture and the Riemann hypothesis are well-known unsolved problems; they have been extensively studied through empirical checks, but remain unproven. The Collatz conjecture has been verified for start values up to about 2.88 × 10¹⁸. The Riemann hypothesis has been verified to hold for the first 10 trillion non-trivial zeroes of the zeta function. Although most mathematicians can tolerate supposing that the conjecture and the hypothesis are true, neither of these propositions is considered proved.

Such evidence does not constitute proof. For example, the Mertens conjecture is a statement about natural numbers that is now known to be false, but no explicit counterexample (i.e., a natural number ''n'' for which the Mertens function ''M''(''n'') equals or exceeds the square root of ''n'') is known: all numbers less than 10¹⁴ have the Mertens property, and the smallest number that does not have this property is only known to be less than the exponential of 1.59 × 10⁴⁰, which is approximately 10 to the power 4.3 × 10³⁹. Since the number of particles in the universe is generally considered less than 10 to the power 100 (a googol), there is no hope to find an explicit counterexample by exhaustive search.

The word "theory" also exists in mathematics, to denote a body of mathematical axioms, definitions and theorems, as in, for example, group theory (see mathematical theory). There are also "theorems" in science, particularly physics, and in engineering, but they often have statements and proofs in which physical assumptions and intuition play an important role; the physical axioms on which such "theorems" are based are themselves falsifiable.

Terminology

A number of different terms for mathematical statements exist; these terms indicate the role statements play in a particular subject. The distinction between different terms is sometimes rather arbitrary, and the usage of some terms has evolved over time.
* An ''axiom'' or ''postulate'' is a fundamental assumption regarding the object of study, that is accepted without proof. A related concept is that of a '' definition'', which gives the meaning of a word or a phrase in terms of known concepts. Classical geometry discerns between axioms, which are general statements; and postulates, which are statements about geometrical objects. Historically, axioms were regarded as "self-evident"; today they are merely ''assumed'' to be true.
* A ''conjecture'' is an unproved statement that is believed to be true. Conjectures are usually made in public, and named after their maker (for example, Goldbach's conjecture and Collatz conjecture). The term ''hypothesis'' is also used in this sense (for example, Riemann hypothesis), which should not be confused with "hypothesis" as the premise of a proof. Other terms are also used on occasion, for example ''problem'' when people are not sure whether the statement should be believed to be true. Fermat's Last Theorem was historically called a theorem, although, for centuries, it was only a conjecture.

* A ''theorem'' is a statement that has been proven to be true based on axioms and other theorems.
* A ''proposition'' is a theorem of lesser importance, or one that is considered so elementary or immediately obvious, that it may be stated without proof. This should not be confused with "proposition" as used in propositional logic. In classical geometry the term "proposition" was used differently: in Euclid's ''Elements'' (), all theorems and geometric constructions were called "propositions" regardless of their importance.
* A ''lemma'' is an "accessory proposition" - a proposition with little applicability outside its use in a particular proof. Over time a lemma may gain in importance and be considered a ''theorem'', though the term "lemma" is usually kept as part of its name (e.g. Gauss's lemma, Zorn's lemma, and the fundamental lemma).
* A ''corollary'' is a proposition that follows immediately from another theorem or axiom, with little or no required proof. A corollary may also be a restatement of a theorem in a simpler form, or for a special case: for example, the theorem "all internal angles in a rectangle are right angles" has a corollary that "all internal angles in a ''square'' are right angles" - a square being a special case of a rectangle.
* A ''generalization'' of a theorem is a theorem with a similar statement but a broader scope, from which the original theorem can be deduced as a special case (a ''corollary'').

Other terms may also be used for historical or customary reasons, for example:

* An '' identity'' is a theorem stating an equality between two expressions, that holds for any value within its domain (e.g. Bézout's identity and Vandermonde's identity).
* A ''rule'' is a theorem that establishes a useful formula (e.g. Bayes' rule and Cramer's rule).
* A ''law'' or ''principle'' is a theorem with wide applicability (e.g. the law of large numbers, law of cosines, Kolmogorov's zero–one law, Harnack's principle, the least-upper-bound principle, and the pigeonhole principle).

A few well-known theorems have even more idiosyncratic names, for example, the division algorithm, Euler's formula, and the Banach–Tarski paradox.

Layout

A theorem and its proof are typically laid out as follows:

:''Theorem'' (name of the person who proved it, along with year of discovery or publication of the proof)
:''Statement of theorem (sometimes called the ''proposition'')''
:''Proof''
:''Description of proof''
:''End''

The end of the proof may be signaled by the letters Q.E.D. (''quod erat demonstrandum'') or by one of the tombstone marks, such as "□" or "∎", meaning "end of proof", introduced by Paul Halmos following their use in magazines to mark the end of an article.

The exact style depends on the author or publication. Many publications provide instructions or macros for typesetting in the house style.

It is common for a theorem to be preceded by definitions describing the exact meaning of the terms used in the theorem. It is also common for a theorem to be preceded by a number of propositions or lemmas which are then used in the proof. However, lemmas are sometimes embedded in the proof of a theorem, either with nested proofs, or with their proofs presented after the proof of the theorem.

Corollaries to a theorem are either presented between the theorem and the proof, or directly after the proof. Sometimes, corollaries have proofs of their own that explain why they follow from the theorem.

Lore

It has been estimated that over a quarter of a million theorems are proved every year.

The well-known aphorism, "A mathematician is a device for turning coffee into theorems", is probably due to Alfréd Rényi, although it is often attributed to Rényi's colleague Paul Erdős (and Rényi may have been thinking of Erdős), who was famous for the many theorems he produced, the number of his collaborations, and his coffee drinking.

The classification of finite simple groups is regarded by some to be the longest proof of a theorem. It comprises tens of thousands of pages in 500 journal articles by some 100 authors. These papers are together believed to give a complete proof, and several ongoing projects hope to shorten and simplify this proof. Another theorem of this type is the four color theorem whose computer generated proof is too long for a human to read. It is among the longest known proofs of a theorem whose statement can be easily understood by a layman.

Theorems in logic

In mathematical logic, a formal theory is a set of sentences within a formal language. A sentence is a well-formed formula with no free variables. A sentence that is a member of a theory is one of its theorems, and the theory is the set of its theorems. Usually a theory is understood to be closed under the relation of logical consequence. Some accounts define a theory to be closed under the semantic consequence relation ($\models$), while others define it to be closed under the syntactic consequence, or derivability relation ($\vdash$).van Dalen, p. 104.

For a theory to be closed under a derivability relation, it must be associated with a deductive system that specifies how the theorems are derived. The deductive system may be stated explicitly, or it may be clear from the context. The closure of the empty set under the relation of logical consequence yields the set that contains just those sentences that are the theorems of the deductive system.

In the broad sense in which the term is used within logic, a theorem does not have to be true, since the theory that contains it may be unsound relative to a given semantics, or relative to the standard interpretation of the underlying language. A theory that is inconsistent has all sentences as theorems.

The definition of theorems as sentences of a formal language is useful within proof theory, which is a branch of mathematics that studies the structure of formal proofs and the structure of provable formulas. It is also important in model theory, which is concerned with the relationship between formal theories and structures that are able to provide a semantics for them through interpretation.

Although theorems may be uninterpreted sentences, in practice mathematicians are more interested in the meanings of the sentences, i.e. in the propositions they express. What makes formal theorems useful and interesting is that they may be interpreted as true propositions and their derivations may be interpreted as a proof of their truth. A theorem whose interpretation is a true statement ''about'' a formal system (as opposed to ''within'' a formal system) is called a '' metatheorem''.

Some important theorems in mathematical logic are:

* Compactness of first-order logic
* Completeness of first-order logic
* Gödel's incompleteness theorems of first-order arithmetic
* Consistency of first-order arithmetic
* Tarski's undefinability theorem
* Church-Turing theorem of undecidability
* Löb's theorem
* Löwenheim–Skolem theorem
* Lindström's theorem
* Craig's theorem
* Cut-elimination theorem

Syntax and semantics

The concept of a formal theorem is fundamentally syntactic, in contrast to the notion of a ''true proposition,'' which introduces semantics. Different deductive systems can yield other interpretations, depending on the presumptions of the derivation rules (i.e. belief, justification or other modalities). The soundness of a formal system depends on whether or not all of its theorems are also validities. A validity is a formula that is true under any possible interpretation (for example, in classical propositional logic, validities are tautologies). A formal system is considered semantically complete when all of its theorems are also tautologies.

Interpretation of a formal theorem

Theorems and theories

See also

* List of theorems
*List of theorems called fundamental
*Formula
*Inference
* Toy theorem

Notes

References

References

*
*
*
*
*
*
*
*
*
*
*
*
*
*
*

External links

*
*
Theorem of the Day

{{Authority control

Logical consequence
Logical expressions
Mathematical proofs
Mathematical terminology
Statements

de:Theorem