Tensor derivative (continuum mechanics)

The derivatives of scalars, vectors, and second-order tensors with respect to second-order tensors are of considerable use in continuum mechanics. These derivatives are used in the theories of nonlinear elasticity and plasticity, particularly in the design of algorithms for numerical simulations.J. C. Simo and T. J. R. Hughes, 1998, ''Computational Inelasticity'', Springer

The directional derivative provides a systematic way of finding these derivatives.J. E. Marsden and T. J. R. Hughes, 2000, ''Mathematical Foundations of Elasticity'', Dover.

Derivatives with respect to vectors and second-order tensors

The definitions of directional derivatives for various situations are given below. It is assumed that the functions are sufficiently smooth that derivatives can be taken.

Derivatives of scalar valued functions of vectors

Let ''f''(v) be a real valued function of the vector v. Then the derivative of ''f''(v) with respect to v (or at v) is the vector defined through its dot product with any vector u being

\frac\cdot\mathbf = Df(\mathbf) mathbf= \left frac~f(\mathbf + \alpha~\mathbf)\right

for all vectors u. The above dot product yields a scalar, and if u is a unit vector gives the directional derivative of ''f'' at v, in the u direction.

Properties:
# If $f(\mathbf) = f_1(\mathbf) + f_2(\mathbf)$ then $\frac\cdot\mathbf = \left(\frac + \frac\right)\cdot\mathbf$
# If $f(\mathbf) = f_1(\mathbf)~ f_2(\mathbf)$ then $\frac\cdot\mathbf = \left(\frac \cdot \mathbf \right)~f_2(\mathbf) + f_1(\mathbf)~\left(\frac\cdot\mathbf \right)$
# If $f(\mathbf) = f_1(f_2(\mathbf))$ then $\frac\cdot\mathbf = \frac~\frac\cdot\mathbf$

Derivatives of vector valued functions of vectors

Let f(v) be a vector valued function of the vector v. Then the derivative of f(v) with respect to v (or at v) is the second order tensor defined through its dot product with any vector u being

\frac\cdot\mathbf = D\mathbf(\mathbf) mathbf= \left frac~\mathbf(\mathbf + \alpha~\mathbf ) \right

for all vectors u. The above dot product yields a vector, and if u is a unit vector gives the direction derivative of f at v, in the directional u.

Properties:
# If $\mathbf(\mathbf) = \mathbf_1(\mathbf) + \mathbf_2(\mathbf)$ then $\frac\cdot\mathbf = \left(\frac + \frac\right)\cdot\mathbf$
# If $\mathbf(\mathbf) = \mathbf_1(\mathbf)\times\mathbf_2(\mathbf)$ then $\frac\cdot\mathbf = \left(\frac\cdot\mathbf\right)\times\mathbf_2(\mathbf) + \mathbf_1(\mathbf)\times\left(\frac\cdot\mathbf \right)$
# If $\mathbf(\mathbf) = \mathbf_1(\mathbf_2(\mathbf))$ then $\frac\cdot\mathbf = \frac\cdot\left(\frac\cdot\mathbf \right)$

Derivatives of scalar valued functions of second-order tensors

Let $f(\boldsymbol)$ be a real valued function of the second order tensor $\boldsymbol$. Then the derivative of $f(\boldsymbol)$ with respect to $\boldsymbol$ (or at $\boldsymbol$) in the direction $\boldsymbol$ is the second order tensor defined as
\frac:\boldsymbol = Df(\boldsymbol) boldsymbol= \left frac~f(\boldsymbol + \alpha~\boldsymbol)\right
for all second order tensors $\boldsymbol$.

Properties:
# If $f(\boldsymbol) = f_1(\boldsymbol) + f_2(\boldsymbol)$ then $\frac:\boldsymbol = \left(\frac + \frac\right):\boldsymbol$
# If $f(\boldsymbol) = f_1(\boldsymbol)~ f_2(\boldsymbol)$ then $\frac:\boldsymbol = \left(\frac:\boldsymbol\right)~f_2(\boldsymbol) + f_1(\boldsymbol)~\left(\frac:\boldsymbol \right)$
# If $f(\boldsymbol) = f_1(f_2(\boldsymbol))$ then $\frac:\boldsymbol = \frac~\left(\frac:\boldsymbol \right)$

Derivatives of tensor valued functions of second-order tensors

Let $\boldsymbol(\boldsymbol)$ be a second order tensor valued function of the second order tensor $\boldsymbol$. Then the derivative of $\boldsymbol(\boldsymbol)$ with respect to $\boldsymbol$ (or at $\boldsymbol$) in the direction $\boldsymbol$ is the fourth order tensor defined as
\frac:\boldsymbol = D\boldsymbol(\boldsymbol) boldsymbol= \left frac~\boldsymbol(\boldsymbol + \alpha~\boldsymbol)\right
for all second order tensors $\boldsymbol$.

Properties:
# If $\boldsymbol(\boldsymbol) = \boldsymbol_1(\boldsymbol) + \boldsymbol_2(\boldsymbol)$ then $\frac:\boldsymbol = \left(\frac + \frac\right):\boldsymbol$
# If $\boldsymbol(\boldsymbol) = \boldsymbol_1(\boldsymbol)\cdot\boldsymbol_2(\boldsymbol)$ then $\frac:\boldsymbol = \left(\frac:\boldsymbol\right)\cdot\boldsymbol_2(\boldsymbol) + \boldsymbol_1 (\boldsymbol) \cdot\left(\frac:\boldsymbol \right)$
# If $\boldsymbol(\boldsymbol) = \boldsymbol_1(\boldsymbol_2(\boldsymbol))$ then $\frac:\boldsymbol = \frac:\left(\frac:\boldsymbol \right)$
# If $f(\boldsymbol) = f_1(\boldsymbol_2(\boldsymbol))$ then $\frac:\boldsymbol = \frac:\left(\frac:\boldsymbol \right)$

Gradient of a tensor field

The gradient, $\boldsymbol\boldsymbol$, of a tensor field $\boldsymbol(\mathbf)$ in the direction of an arbitrary constant vector c is defined as:
$\boldsymbol\boldsymbol\cdot\mathbf = \lim_ \quad \cfrac~\boldsymbol(\mathbf+\alpha\mathbf)$
The gradient of a tensor field of order ''n'' is a tensor field of order ''n''+1.

Cartesian coordinates

If $\mathbf_1,\mathbf_2,\mathbf_3$ are the basis vectors in a Cartesian coordinate system, with coordinates of points denoted by ($x_1, x_2, x_3$), then the gradient of the tensor field $\boldsymbol$ is given by
$\boldsymbol\boldsymbol = \cfrac \otimes \mathbf_i$

Since the basis vectors do not vary in a Cartesian coordinate system we have the following relations for the gradients of a scalar field $\phi$, a vector field v, and a second-order tensor field $\boldsymbol$.
$\begin \boldsymbol\phi & = \cfrac~\mathbf_i = \phi_ ~\mathbf_i \\ \boldsymbol\mathbf & = \cfrac\otimes\mathbf_i = \cfrac~\mathbf_j\otimes\mathbf_i = v_~\mathbf_j\otimes\mathbf_i \\ \boldsymbol\boldsymbol & = \cfrac\otimes\mathbf_i = \cfrac~\mathbf_j\otimes\mathbf_k\otimes\mathbf_i = S_~\mathbf_j\otimes\mathbf_k\otimes\mathbf_i \end$

Curvilinear coordinates

If $\mathbf^1,\mathbf^2,\mathbf^3$ are the contravariant basis vectors in a curvilinear coordinate system, with coordinates of points denoted by ($\xi^1, \xi^2, \xi^3$), then the gradient of the tensor field $\boldsymbol$ is given by (see Ogden, R. W., 2000, Nonlinear Elastic Deformations, Dover. for a proof.)
$\boldsymbol\boldsymbol = \frac\otimes\mathbf^i$

From this definition we have the following relations for the gradients of a scalar field $\phi$, a vector field v, and a second-order tensor field $\boldsymbol$.
$\begin \boldsymbol\phi & = \frac~\mathbf^i \\ \boldsymbol\mathbf & = \frac\otimes\mathbf^i = \left(\frac + v^k~\Gamma_^j\right)~\mathbf_j\otimes\mathbf^i = \left(\frac - v_k~\Gamma_^k\right)~\mathbf^j\otimes\mathbf^i \\ \boldsymbol\boldsymbol & = \frac\otimes\mathbf^i = \left(\frac - S_~\Gamma_^l - S_~\Gamma_^l\right)~\mathbf^j\otimes\mathbf^k\otimes\mathbf^i \end$

where the Christoffel symbol $\Gamma_^k$ is defined using
$\Gamma_^k~\mathbf_k = \frac \quad \implies \quad \Gamma_^k = \frac\cdot\mathbf^k = -\mathbf_i\cdot\frac$

Cylindrical polar coordinates

In cylindrical coordinates, the gradient is given by
\begin
\boldsymbol\phi =\quad
&\frac~\mathbf_r
+ \frac~\frac~\mathbf_\theta
+ \frac~\mathbf_z \\

\boldsymbol\mathbf =\quad
&\frac~\mathbf_r \otimes \mathbf_r
+ \frac\left(\frac - v_\theta\right)~\mathbf_r \otimes \mathbf_\theta
+ \frac~\mathbf_r \otimes \mathbf_z \\
+ &\frac~\mathbf_\theta \otimes \mathbf_r
+ \frac\left(\frac + v_r\right)~\mathbf_\theta \otimes \mathbf_\theta
+ \frac~\mathbf_\theta \otimes \mathbf_z \\
+ &\frac~\mathbf_z\otimes\mathbf_r
+ \frac\frac~\mathbf_z \otimes\mathbf_\theta
+ \frac~\mathbf_z\otimes\mathbf_z \\

\boldsymbol\boldsymbol =\quad
&\frac~\mathbf_r\otimes\mathbf_r\otimes\mathbf_r
+ \frac~\mathbf_r \otimes \mathbf_r \otimes \mathbf_z
+ \frac\left frac - (S_ + S_)\right\mathbf_r \otimes \mathbf_r\otimes\mathbf_\theta \\
+ &\frac~\mathbf_r \otimes \mathbf_\theta \otimes \mathbf_r
+ \frac~\mathbf_r \otimes \mathbf_\theta \otimes \mathbf_z
+ \frac\left frac + (S_ - S_)\right\mathbf_r \otimes \mathbf_\theta \otimes \mathbf_\theta \\
+ &\frac~\mathbf_r \otimes \mathbf_z \otimes \mathbf_r
+ \frac~\mathbf_r \otimes \mathbf_z \otimes \mathbf_z
+ \frac\left frac - S_\right\mathbf_r \otimes \mathbf_z \otimes \mathbf_\theta \\
+ &\frac~\mathbf_\theta \otimes \mathbf_r \otimes \mathbf_r
+ \frac~\mathbf_\theta \otimes \mathbf_r \otimes \mathbf_z
+ \frac\left frac + (S_ - S_)\right\mathbf_\theta \otimes \mathbf_r \otimes \mathbf_\theta \\
+ &\frac~\mathbf_\theta \otimes \mathbf_\theta \otimes \mathbf_r
+ \frac~\mathbf_\theta \otimes \mathbf_\theta \otimes \mathbf_z
+ \frac\left frac + (S_ + S_)\right\mathbf_\theta \otimes \mathbf_\theta \otimes \mathbf_\theta \\
+ &\frac~\mathbf_\theta \otimes \mathbf_z \otimes \mathbf_r
+ \frac~\mathbf_\theta \otimes \mathbf_z \otimes \mathbf_z
+ \frac\left frac + S_\right\mathbf_\theta \otimes \mathbf_z \otimes \mathbf_\theta \\
+ &\frac~\mathbf_z \otimes \mathbf_r \otimes \mathbf_r
+ \frac~\mathbf_z \otimes \mathbf_r \otimes \mathbf_z
+ \frac\left frac - S_\right\mathbf_z \otimes \mathbf_r \otimes \mathbf_\theta \\
+ &\frac~\mathbf_z \otimes \mathbf_\theta \otimes \mathbf_r
+ \frac~\mathbf_z \otimes \mathbf_\theta \otimes \mathbf_z
+ \frac\left frac + S_\right\mathbf_z \otimes \mathbf_\theta \otimes \mathbf_\theta \\
+ &\frac~\mathbf_z \otimes \mathbf_z \otimes \mathbf_r
+ \frac~\mathbf_z \otimes \mathbf_z \otimes \mathbf_z
+ \frac~\frac~ \mathbf_z \otimes \mathbf_z \otimes \mathbf_\theta
\end

Divergence of a tensor field

The divergence of a tensor field $\boldsymbol(\mathbf)$ is defined using the recursive relation
$(\boldsymbol\cdot\boldsymbol)\cdot\mathbf = \boldsymbol\cdot\left(\mathbf\cdot\boldsymbol^\textsf\right) ~;\qquad \boldsymbol\cdot\mathbf = \text(\boldsymbol\mathbf)$

where c is an arbitrary constant vector and v is a vector field. If $\boldsymbol$ is a tensor field of order ''n'' > 1 then the divergence of the field is a tensor of order ''n''− 1.

Cartesian coordinates

In a Cartesian coordinate system we have the following relations for a vector field v and a second-order tensor field $\boldsymbol$.
$\begin \boldsymbol\cdot\mathbf &= \frac = v_ \\ \boldsymbol\cdot\boldsymbol &= \frac~\mathbf_k = S_~\mathbf_k \end$

where tensor index notation for partial derivatives is used in the rightmost expressions. Note that
$\boldsymbol\cdot\boldsymbol \neq \boldsymbol\cdot\boldsymbol^\textsf.$

For a symmetric second-order tensor, the divergence is also often written as

$\begin \boldsymbol\cdot\boldsymbol &= \cfrac~\mathbf_k = S_~\mathbf_k \end$

The above expression is sometimes used as the definition of
$\boldsymbol\cdot\boldsymbol$ in Cartesian component form (often also written as
$\operatorname\boldsymbol$). Note that such a definition is not consistent with the rest of this article (see the section on curvilinear co-ordinates).

The difference stems from whether the differentiation is performed with respect to the rows or columns of $\boldsymbol$, and is conventional. This is demonstrated by an example. In a Cartesian coordinate system the second order tensor (matrix) $\mathbf$ is the gradient of a vector function $\mathbf$.

\begin
\boldsymbol \cdot \left( \boldsymbol \mathbf \right) &=
\boldsymbol \cdot \left( v_ ~\mathbf_i \otimes \mathbf_j \right) =
v_ ~\mathbf_i \cdot \mathbf_i \otimes \mathbf_j =
\left( \boldsymbol \cdot \mathbf \right)_ ~\mathbf_j =
\boldsymbol \left( \boldsymbol \cdot \mathbf \right) \\

\boldsymbol \cdot \left \left( \boldsymbol \mathbf \right)^\textsf \right&=
\boldsymbol \cdot \left( v_ ~\mathbf_i \otimes \mathbf_j \right) =
v_ ~\mathbf_i \cdot \mathbf_i \otimes \mathbf_j =
\boldsymbol^ v_ ~\mathbf_j =
\boldsymbol^ \mathbf
\end

The last equation is equivalent to the alternative definition / interpretation

$\begin \left( \boldsymbol \cdot \right)_\text \left( \boldsymbol \mathbf \right) = \left( \boldsymbol \cdot \right)_\text \left( v_ ~\mathbf_i \otimes \mathbf_j \right) = v_ ~\mathbf_i \otimes \mathbf_j \cdot \mathbf_j = \boldsymbol^2 v_i ~\mathbf_i = \boldsymbol^2 \mathbf \end$

Curvilinear coordinates

In curvilinear coordinates, the divergences of a vector field v and a second-order tensor field $\boldsymbol$ are
$\begin \boldsymbol\cdot\mathbf &= \left(\cfrac + v^k~\Gamma_^i\right)\\ \boldsymbol\cdot\boldsymbol &= \left(\cfrac- S_~\Gamma_^l - S_~\Gamma_^l\right)~\mathbf^k \end$

More generally,
\begin
\boldsymbol\cdot\boldsymbol & = \left cfrac - \Gamma^l_~S_ - \Gamma^l_~S_\rightg^~\mathbf^j \\ pt & = \left cfrac + \Gamma^i_~S^ + \Gamma^j_~S^\right\mathbf_j \\ pt & = \left cfrac + \Gamma^i_~S^l_ - \Gamma^l_~S^i_\right\mathbf^j \\ pt & = \left cfrac - \Gamma^l_~S_l^ + \Gamma^j_~S_i^\rightg^~\mathbf_j
\end

Cylindrical polar coordinates

In cylindrical polar coordinates
\begin
\boldsymbol\cdot\mathbf =\quad
&\frac
+ \frac\left(\frac + v_r \right)
+ \frac\\

\boldsymbol\cdot\boldsymbol =\quad
&\frac~\mathbf_r
+ \frac~\mathbf_\theta
+ \frac~\mathbf_z \\

+ &\frac\left frac
+ (S_ - S_)\right\mathbf_r
+ \frac\left frac
+ (S_ + S_)\right\mathbf_\theta
+ \frac\left frac + S_\right\mathbf_z \\

+ &\frac~\mathbf_r
+ \frac~\mathbf_\theta
+ \frac~\mathbf_z
\end

Curl of a tensor field

The curl of an order-''n'' > 1 tensor field $\boldsymbol(\mathbf)$ is also defined using the recursive relation
$(\boldsymbol\times\boldsymbol)\cdot\mathbf = \boldsymbol\times(\mathbf\cdot\boldsymbol) ~;\qquad (\boldsymbol\times\mathbf)\cdot\mathbf = \boldsymbol\cdot(\mathbf\times\mathbf)$
where c is an arbitrary constant vector and v is a vector field.

Curl of a first-order tensor (vector) field

Consider a vector field v and an arbitrary constant vector c. In index notation, the cross product is given by
$\mathbf \times \mathbf = \varepsilon_~v_j~c_k~\mathbf_i$
where $\varepsilon_$ is the permutation symbol, otherwise known as the Levi-Civita symbol. Then,
$\boldsymbol\cdot(\mathbf \times \mathbf) = \varepsilon_~v_~c_k = (\varepsilon_~v_~\mathbf_k)\cdot\mathbf = (\boldsymbol\times\mathbf)\cdot\mathbf$
Therefore,
$\boldsymbol\times\mathbf = \varepsilon_~v_~\mathbf_k$

Curl of a second-order tensor field

For a second-order tensor $\boldsymbol$
$\mathbf\cdot\boldsymbol = c_m~S_~\mathbf_j$
Hence, using the definition of the curl of a first-order tensor field,
$\boldsymbol\times(\mathbf\cdot\boldsymbol) = \varepsilon_~c_m~S_~\mathbf_k = (\varepsilon_~S_~\mathbf_k\otimes\mathbf_m)\cdot\mathbf = (\boldsymbol\times\boldsymbol) \cdot \mathbf$
Therefore, we have
$\boldsymbol\times\boldsymbol = \varepsilon_~S_~\mathbf_k\otimes\mathbf_m$

Identities involving the curl of a tensor field

The most commonly used identity involving the curl of a tensor field, $\boldsymbol$, is
$\boldsymbol\times(\boldsymbol\boldsymbol) = \boldsymbol$
This identity holds for tensor fields of all orders. For the important case of a second-order tensor, $\boldsymbol$, this identity implies that
$\boldsymbol\times(\boldsymbol\boldsymbol) = \boldsymbol \quad \implies \quad S_ - S_ = 0$

Derivative of the determinant of a second-order tensor

The derivative of the determinant of a second order tensor $\boldsymbol$ is given by

\frac\det(\boldsymbol) = \det(\boldsymbol)~\left boldsymbol^\right\textsf ~.

In an orthonormal basis, the components of $\boldsymbol$ can be written as a matrix A. In that case, the right hand side corresponds the cofactors of the matrix.

Derivatives of the invariants of a second-order tensor

The principal invariants of a second order tensor are

\begin
I_1(\boldsymbol) & = \text \\
I_2(\boldsymbol) & = \frac \left (\text)^2 - \text \right\\
I_3(\boldsymbol) & = \det(\boldsymbol)
\end

The derivatives of these three invariants with respect to $\boldsymbol$ are

\begin
\frac & = \boldsymbol \\ pt \frac & = I_1~\boldsymbol - \boldsymbol^\textsf \\ pt \frac & = \det(\boldsymbol)~\left boldsymbol^\right\textsf
= I_2~\boldsymbol - \boldsymbol^\textsf~\left(I_1~\boldsymbol - \boldsymbol^\textsf\right)
= \left(\boldsymbol^2 - I_1~\boldsymbol + I_2~\boldsymbol\right)^\textsf
\end

= \det(\boldsymbol)~\left boldsymbol^\right\textsf ~.

For the derivatives of the other two invariants, let us go back to the characteristic equation
$\det(\lambda~\boldsymbol + \boldsymbol) = \lambda^3 + I_1(\boldsymbol)~\lambda^2 + I_2(\boldsymbol)~\lambda + I_3(\boldsymbol) ~.$

Using the same approach as for the determinant of a tensor, we can show that

\frac\det(\lambda~\boldsymbol + \boldsymbol) =
\det(\lambda~\boldsymbol + \boldsymbol)~\left \lambda~\boldsymbol + \boldsymbol)^\right\textsf ~.

Now the left hand side can be expanded as

\begin
\frac\det(\lambda~\boldsymbol + \boldsymbol) & =
\frac\left \lambda^3 + I_1(\boldsymbol)~\lambda^2 + I_2(\boldsymbol)~\lambda + I_3(\boldsymbol) \right\\
& =
\frac~\lambda^2 + \frac~\lambda +
\frac~.
\end

Hence

\frac~\lambda^2 + \frac~\lambda +
\frac =
\det(\lambda~\boldsymbol + \boldsymbol)~\left \lambda~\boldsymbol + \boldsymbol)^\right\textsf

or,

(\lambda~\boldsymbol + \boldsymbol)^\textsf\cdot\left \frac~\lambda^2 + \frac~\lambda +
\frac\right=
\det(\lambda~\boldsymbol + \boldsymbol)~\boldsymbol ~.

Expanding the right hand side and separating terms on the left hand side gives

\left(\lambda~\boldsymbol +\boldsymbol^\textsf\right)\cdot\left \frac~\lambda^2 + \frac~\lambda +
\frac\right=
\left lambda^3 + I_1~\lambda^2 + I_2~\lambda + I_3\right \boldsymbol

or,

\begin
\left frac~\lambda^3 \right.&
\left.+ \frac~\lambda^2 +
\frac~\lambda\rightboldsymbol +
\boldsymbol^\textsf\cdot\frac~\lambda^2 +
\boldsymbol^\textsf\cdot\frac~\lambda +
\boldsymbol^\textsf\cdot\frac \\
& =
\left lambda^3 + I_1~\lambda^2 + I_2~\lambda + I_3\right \boldsymbol ~.
\end

If we define $I_0 := 1$ and $I_4 := 0$, we can write the above as

\begin
\left frac~\lambda^3 \right.&
\left.+ \frac~\lambda^2 +
\frac~\lambda + \frac\rightboldsymbol +
\boldsymbol^\textsf\cdot\frac~\lambda^3 +
\boldsymbol^\textsf\cdot\frac~\lambda^2 +
\boldsymbol^\textsf\cdot\frac~\lambda +
\boldsymbol^\textsf\cdot\frac \\
&=
\left _0~\lambda^3 + I_1~\lambda^2 + I_2~\lambda + I_3\right \boldsymbol ~.
\end

Collecting terms containing various powers of λ, we get
$\begin \lambda^3&\left(I_0~\boldsymbol - \frac~\boldsymbol - \boldsymbol^\textsf\cdot\frac\right) + \lambda^2\left(I_1~\boldsymbol - \frac~\boldsymbol - \boldsymbol^\textsf\cdot\frac\right) + \\ &\qquad \qquad\lambda\left(I_2~\boldsymbol - \frac~\boldsymbol - \boldsymbol^\textsf\cdot\frac\right) + \left(I_3~\boldsymbol - \frac~\boldsymbol - \boldsymbol^\textsf\cdot\frac\right) = 0 ~. \end$

Then, invoking the arbitrariness of λ, we have
$\begin I_0~\boldsymbol - \frac~\boldsymbol - \boldsymbol^\textsf\cdot\frac & = 0 \\ I_1~\boldsymbol - \frac~\boldsymbol - I_2~\boldsymbol - \frac~\boldsymbol - \boldsymbol^\textsf\cdot\frac & = 0 \\ I_3~\boldsymbol - \frac~\boldsymbol - \boldsymbol^\textsf\cdot\frac & = 0 ~. \end$

This implies that
$\begin \frac &= \boldsymbol \\ \frac & = I_1~\boldsymbol - \boldsymbol^\textsf \\ \frac & = I_2~\boldsymbol - \boldsymbol^\textsf~\left(I_1~\boldsymbol - \boldsymbol^\textsf\right) = \left(\boldsymbol^2 -I_1~\boldsymbol + I_2~\boldsymbol\right)^\textsf \end$

Derivative of the second-order identity tensor

Let $\boldsymbol$ be the second order identity tensor. Then the derivative of this tensor with respect to a second order tensor $\boldsymbol$ is given by
$\frac:\boldsymbol = \boldsymbol:\boldsymbol = \boldsymbol$
This is because $\boldsymbol$ is independent of $\boldsymbol$.

Derivative of a second-order tensor with respect to itself

Let $\boldsymbol$ be a second order tensor. Then

\frac:\boldsymbol =
\left frac (\boldsymbol + \alpha~\boldsymbol)\right =
\boldsymbol =
\boldsymbol:\boldsymbol

Therefore,
$\frac = \boldsymbol$

Here $\boldsymbol$ is the fourth order identity tensor. In index notation with respect to an orthonormal basis
$\boldsymbol = \delta_~\delta_~\mathbf_i\otimes\mathbf_j\otimes\mathbf_k\otimes\mathbf_l$

This result implies that
$\frac:\boldsymbol = \boldsymbol^\textsf:\boldsymbol = \boldsymbol^\textsf$
where
$\boldsymbol^\textsf = \delta_~\delta_~\mathbf_i\otimes\mathbf_j\otimes\mathbf_k\otimes\mathbf_l$

Therefore, if the tensor $\boldsymbol$ is symmetric, then the derivative is also symmetric and we get
$\frac = \boldsymbol^ = \frac~\left(\boldsymbol + \boldsymbol^\textsf\right)$
where the symmetric fourth order identity tensor is
$\boldsymbol^ = \frac~(\delta_~\delta_ + \delta_~\delta_) ~\mathbf_i\otimes\mathbf_j\otimes\mathbf_k\otimes\mathbf_l$

Derivative of the inverse of a second-order tensor

Let $\boldsymbol$ and $\boldsymbol$ be two second order tensors, then
$\frac \left(\boldsymbol^\right) : \boldsymbol = - \boldsymbol^\cdot\boldsymbol\cdot\boldsymbol^$
In index notation with respect to an orthonormal basis
$\frac~T_ = - A^_~T_~A^_ \implies \frac = - A^_~A^_$
We also have
$\frac \left(\boldsymbol^\right) : \boldsymbol = - \boldsymbol^\cdot\boldsymbol^\textsf\cdot\boldsymbol^$
In index notation
$\frac~T_ = - A^_~T_~A^_ \implies \frac = - A^_~A^_$
If the tensor $\boldsymbol$ is symmetric then
$\frac = -\cfrac\left(A^_~A^_ + A^_~A^_\right)$

}:\boldsymbol = \boldsymbol

Since $\boldsymbol^\cdot\boldsymbol = \boldsymbol$, we can write
$\frac\left(\boldsymbol^\cdot\boldsymbol\right):\boldsymbol = \boldsymbol$

Using the product rule for second order tensors

\frac boldsymbol_1(\boldsymbol)\cdot\boldsymbol_2(\boldsymbol)\boldsymbol =
\left(\frac:\boldsymbol\right)\cdot\boldsymbol_2 +
\boldsymbol_1\cdot\left(\frac:\boldsymbol\right)

we get
$\frac(\boldsymbol^\cdot\boldsymbol):\boldsymbol = \left(\frac:\boldsymbol\right)\cdot\boldsymbol + \boldsymbol^\cdot\left(\frac:\boldsymbol\right) = \boldsymbol$
or,
$\left(\frac:\boldsymbol\right)\cdot\boldsymbol = - \boldsymbol^\cdot\boldsymbol$

Therefore,
$\frac \left(\boldsymbol^\right) : \boldsymbol = - \boldsymbol^\cdot\boldsymbol\cdot\boldsymbol^$

Integration by parts

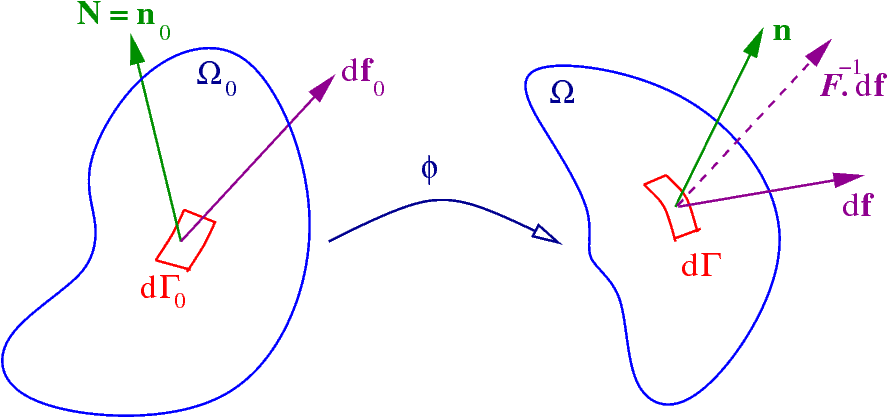
Another important operation related to tensor derivatives in continuum mechanics is integration by parts. The formula for integration by parts can be written as
$\int_ \boldsymbol\otimes\boldsymbol\boldsymbol\,d\Omega = \int_ \mathbf \otimes (\boldsymbol\otimes\boldsymbol)\,d\Gamma - \int_ \boldsymbol\otimes\boldsymbol\boldsymbol\,d\Omega$

where $\boldsymbol$ and $\boldsymbol$ are differentiable tensor fields of arbitrary order, $\mathbf$ is the unit outward normal to the domain over which the tensor fields are defined, $\otimes$ represents a generalized tensor product operator, and $\boldsymbol$ is a generalized gradient operator. When $\boldsymbol$ is equal to the identity tensor, we get the divergence theorem
$\int_\boldsymbol\boldsymbol\,d\Omega = \int_ \mathbf\otimes\boldsymbol\,d\Gamma \,.$

We can express the formula for integration by parts in Cartesian index notation as
$\int_ F_\,G_\,d\Omega = \int_ n_p\,F_\,G_\,d\Gamma - \int_ G_\,F_\,d\Omega \,.$

For the special case where the tensor product operation is a contraction of one index and the gradient operation is a divergence, and both $\boldsymbol$ and $\boldsymbol$ are second order tensors, we have
$\int_ \boldsymbol\cdot(\boldsymbol\cdot\boldsymbol)\,d\Omega = \int_ \mathbf\cdot\left(\boldsymbol\cdot\boldsymbol^\textsf\right)\,d\Gamma - \int_ (\boldsymbol\boldsymbol):\boldsymbol^\textsf\,d\Omega \,.$

In index notation,
$\int_ F_\,G_\,d\Omega = \int_ n_p\,F_\,G_\,d\Gamma - \int_ G_\,F_\,d\Omega \,.$

See also

* Covariant derivative
* Ricci calculus

References

{{Reflist

Solid mechanics
Mechanics