Tunstall Coding on:
[Wikipedia]
[Google]
[Amazon]
In
Study of Tunstall's algorithm from EPFL's Information Theory department
 We then take the leaf of highest probability (here, ), and convert it to yet another tree of leaves, one for each character.
We re-compute the probabilities of those leaves. For instance, the sequence of two letters L happens once.
Given that there are three occurrences of letters followed by an L, the resulting probability is .
We obtain 17 words, which can each be encoded into a fixed-sized output of bits.
We then take the leaf of highest probability (here, ), and convert it to yet another tree of leaves, one for each character.
We re-compute the probabilities of those leaves. For instance, the sequence of two letters L happens once.
Given that there are three occurrences of letters followed by an L, the resulting probability is .
We obtain 17 words, which can each be encoded into a fixed-sized output of bits.
 Note that we could iterate further, increasing the number of words by every time.
Note that we could iterate further, increasing the number of words by every time.
 This is an example of a Tunstall code being used to read ( for transmit ) any data that is scrambled, e.g. by polynomial scrambling. This particular example helps to modify the base of the data from 2 to 3 in a stream therefore avoiding expensive base modification routines. With base modification we are particularly bound by 'efficiency' of reads, where ideally bits are used at an average to read the code. This ensures that upon use of the new base, which is duty bound to use at best bits per code, our reads do not result in lesser margin of efficiency of transmission for which we are employing the base modification in the first place. We can therefore then employ the read-to-modify-base mechanism for efficiently transmitting the data across channels that have a different base. eg. transmitting binary data across say MLT-3 channels with increased efficiency when compared to mapping codes ( with large number of unused codes ).
We are essentially reading perfectly scrambled binary data or 'implied data' for the purpose of transmitting it using base-3 channels. Please see leaf nodes in the Ternary Tunstall Tree. As we can see, the read will result in the first digit being 'B' - 25% of the time as it has an implied probability of 25%, being of length 2 trying to read from implied data. A 'B' such read does not read any further, but with 75% probability we read 'A' or 'C', requiring another code. Thus the efficiency of the read is 2.75 ( average length of the size 7 Huffman code ) / 1.75 ( average length of the 1 or 2-digit base - 3 Tunstall code ) = which is as per requirement very close to which calculates to an efficiency of . We can then transmit the symbols using base-3 channels efficiently.
This is an example of a Tunstall code being used to read ( for transmit ) any data that is scrambled, e.g. by polynomial scrambling. This particular example helps to modify the base of the data from 2 to 3 in a stream therefore avoiding expensive base modification routines. With base modification we are particularly bound by 'efficiency' of reads, where ideally bits are used at an average to read the code. This ensures that upon use of the new base, which is duty bound to use at best bits per code, our reads do not result in lesser margin of efficiency of transmission for which we are employing the base modification in the first place. We can therefore then employ the read-to-modify-base mechanism for efficiently transmitting the data across channels that have a different base. eg. transmitting binary data across say MLT-3 channels with increased efficiency when compared to mapping codes ( with large number of unused codes ).
We are essentially reading perfectly scrambled binary data or 'implied data' for the purpose of transmitting it using base-3 channels. Please see leaf nodes in the Ternary Tunstall Tree. As we can see, the read will result in the first digit being 'B' - 25% of the time as it has an implied probability of 25%, being of length 2 trying to read from implied data. A 'B' such read does not read any further, but with 75% probability we read 'A' or 'C', requiring another code. Thus the efficiency of the read is 2.75 ( average length of the size 7 Huffman code ) / 1.75 ( average length of the 1 or 2-digit base - 3 Tunstall code ) = which is as per requirement very close to which calculates to an efficiency of . We can then transmit the symbols using base-3 channels efficiently.
computer science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ...
and information theory
Information theory is the mathematical study of the quantification (science), quantification, Data storage, storage, and telecommunications, communication of information. The field was established and formalized by Claude Shannon in the 1940s, ...
, Tunstall coding is a form of entropy coding
In information theory, an entropy coding (or entropy encoding) is any lossless data compression method that attempts to approach the lower bound declared by Shannon's source coding theorem, which states that any lossless data compression method ...
used for lossless data compression
Lossless compression is a class of data compression that allows the original data to be perfectly reconstructed from the compressed data with no loss of information. Lossless compression is possible because most real-world data exhibits Redundanc ...
.
History
Tunstall coding was the subject of Brian Parker Tunstall's PhD thesis in 1967, while at Georgia Institute of Technology. The subject of that thesis was "Synthesis of noiseless compression codes" Its design is a precursor toLempel–Ziv
LZ77 and LZ78 are the two lossless data compression algorithms published in papers by Abraham Lempel and Jacob Ziv in 1977 and 1978.
They are also known as Lempel-Ziv 1 (LZ1) and Lempel-Ziv 2 (LZ2) respectively. These two algorithms form the bas ...
.
Properties
Unlikevariable-length code
In coding theory, a variable-length code is a code which maps source symbols to a ''variable'' number of bits. The equivalent concept in computer science is '' bit string''.
Variable-length codes can allow sources to be compressed and decompr ...
s, which include Huffman and Lempel–Ziv coding
LZ77 and LZ78 are the two lossless data compression algorithms published in papers by Abraham Lempel and Jacob Ziv in 1977 and 1978.
They are also known as Lempel-Ziv 1 (LZ1) and Lempel-Ziv 2 (LZ2) respectively. These two algorithms form the basis ...
,
Tunstall coding is a code
In communications and information processing, code is a system of rules to convert information—such as a letter, word, sound, image, or gesture—into another form, sometimes shortened or secret, for communication through a communicati ...
which maps source symbols to a fixed number of bits.
Both Tunstall codes and Lempel–Ziv codes represent variable-length words by fixed-length codes.
Unlike typical set encoding, Tunstall coding parses a stochastic source with codewords of variable length.
It can be shown that, for a large enough dictionary, the number of bits per source letter can be arbitrarily close to , the entropy
Entropy is a scientific concept, most commonly associated with states of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the micros ...
of the source.Study of Tunstall's algorithm from EPFL's Information Theory department
Algorithm
The algorithm requires as input an input alphabet , along with a distribution of probabilities for each word input. It also requires an arbitrary constant , which is an upper bound to the size of the dictionary that it will compute. The dictionary in question, , is constructed as a tree of probabilities, in which each edge is associated to a letter from the input alphabet. The algorithm goes like this: D := tree of leaves, one for each letter in . While : Convert most probable leaf to tree with leaves.Example
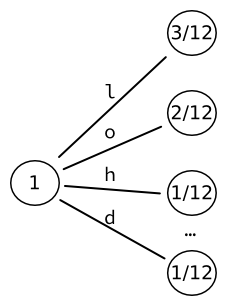
Let's imagine that we wish to encode the string "hello, world". Let's further assume (somewhat unrealistically) that the input alphabet contains only characters from the string "hello, world" — that is, 'h', 'e', 'l', ',', ' ', 'w', 'o', 'r', 'd'. We can therefore compute the probability of each character based on its statistical appearance in the input string. For instance, the letter L appears thrice in a string of 12 characters: its probability is . We initialize the tree, starting with a tree of leaves. Each word is therefore directly associated to a letter of the alphabet. The 9 words that we thus obtain can be encoded into a fixed-sized output of bits. We then take the leaf of highest probability (here, ), and convert it to yet another tree of leaves, one for each character.
We re-compute the probabilities of those leaves. For instance, the sequence of two letters L happens once.
Given that there are three occurrences of letters followed by an L, the resulting probability is .
We obtain 17 words, which can each be encoded into a fixed-sized output of bits.
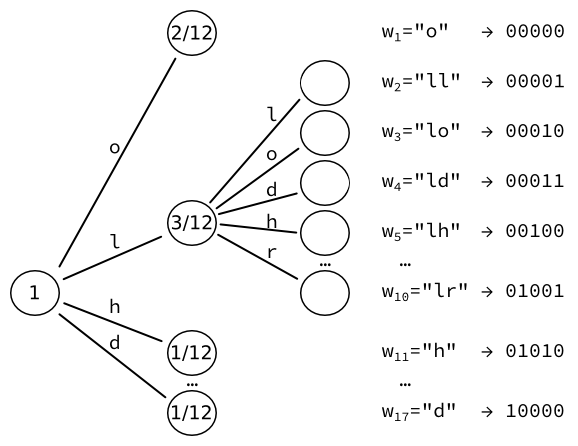
We then take the leaf of highest probability (here, ), and convert it to yet another tree of leaves, one for each character.
We re-compute the probabilities of those leaves. For instance, the sequence of two letters L happens once.
Given that there are three occurrences of letters followed by an L, the resulting probability is .
We obtain 17 words, which can each be encoded into a fixed-sized output of bits.
 Note that we could iterate further, increasing the number of words by every time.
Note that we could iterate further, increasing the number of words by every time.
Limitations
Tunstall coding requires the algorithm to know, prior to the parsing operation, what the distribution of probabilities for each letter of the alphabet is. This issue is shared withHuffman coding
In computer science and information theory, a Huffman code is a particular type of optimal prefix code that is commonly used for lossless data compression. The process of finding or using such a code is Huffman coding, an algorithm developed by ...
.
Its requiring a fixed-length block output makes it lesser than Lempel–Ziv
LZ77 and LZ78 are the two lossless data compression algorithms published in papers by Abraham Lempel and Jacob Ziv in 1977 and 1978.
They are also known as Lempel-Ziv 1 (LZ1) and Lempel-Ziv 2 (LZ2) respectively. These two algorithms form the bas ...
, which has a similar dictionary-based design, but with a variable-sized block output.
Implied Read for base modification
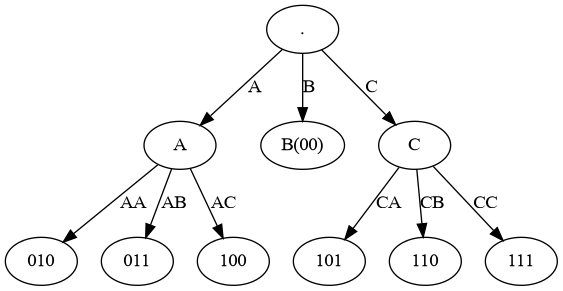
 This is an example of a Tunstall code being used to read ( for transmit ) any data that is scrambled, e.g. by polynomial scrambling. This particular example helps to modify the base of the data from 2 to 3 in a stream therefore avoiding expensive base modification routines. With base modification we are particularly bound by 'efficiency' of reads, where ideally bits are used at an average to read the code. This ensures that upon use of the new base, which is duty bound to use at best bits per code, our reads do not result in lesser margin of efficiency of transmission for which we are employing the base modification in the first place. We can therefore then employ the read-to-modify-base mechanism for efficiently transmitting the data across channels that have a different base. eg. transmitting binary data across say MLT-3 channels with increased efficiency when compared to mapping codes ( with large number of unused codes ).
We are essentially reading perfectly scrambled binary data or 'implied data' for the purpose of transmitting it using base-3 channels. Please see leaf nodes in the Ternary Tunstall Tree. As we can see, the read will result in the first digit being 'B' - 25% of the time as it has an implied probability of 25%, being of length 2 trying to read from implied data. A 'B' such read does not read any further, but with 75% probability we read 'A' or 'C', requiring another code. Thus the efficiency of the read is 2.75 ( average length of the size 7 Huffman code ) / 1.75 ( average length of the 1 or 2-digit base - 3 Tunstall code ) = which is as per requirement very close to which calculates to an efficiency of . We can then transmit the symbols using base-3 channels efficiently.
This is an example of a Tunstall code being used to read ( for transmit ) any data that is scrambled, e.g. by polynomial scrambling. This particular example helps to modify the base of the data from 2 to 3 in a stream therefore avoiding expensive base modification routines. With base modification we are particularly bound by 'efficiency' of reads, where ideally bits are used at an average to read the code. This ensures that upon use of the new base, which is duty bound to use at best bits per code, our reads do not result in lesser margin of efficiency of transmission for which we are employing the base modification in the first place. We can therefore then employ the read-to-modify-base mechanism for efficiently transmitting the data across channels that have a different base. eg. transmitting binary data across say MLT-3 channels with increased efficiency when compared to mapping codes ( with large number of unused codes ).
We are essentially reading perfectly scrambled binary data or 'implied data' for the purpose of transmitting it using base-3 channels. Please see leaf nodes in the Ternary Tunstall Tree. As we can see, the read will result in the first digit being 'B' - 25% of the time as it has an implied probability of 25%, being of length 2 trying to read from implied data. A 'B' such read does not read any further, but with 75% probability we read 'A' or 'C', requiring another code. Thus the efficiency of the read is 2.75 ( average length of the size 7 Huffman code ) / 1.75 ( average length of the 1 or 2-digit base - 3 Tunstall code ) = which is as per requirement very close to which calculates to an efficiency of . We can then transmit the symbols using base-3 channels efficiently.
References
{{Compression methods Lossless compression algorithms Data compression