Truncated cube

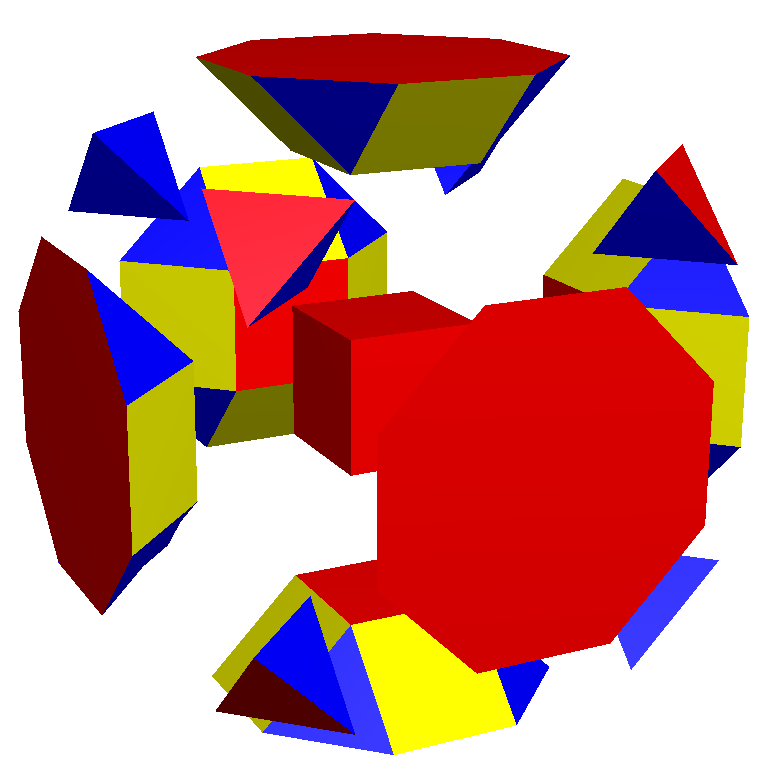In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces (6 octagonal and 8 triangular), 36 edges, and 24 vertices.

If the truncated cube has unit edge length, its dual triakis octahedron has edges of lengths and ,
where ''δ_S'' is the silver ratio, +1.

Area and volume

The area ''A'' and the volume ''V'' of a truncated cube of edge length ''a'' are:
:$\begin A &= 2\left(6+6\sqrt+\sqrt\right)a^2 &&\approx 32.434\,6644a^2 \\ V &= \fraca^3 &&\approx 13.599\,6633a^3. \end$

Orthogonal projections

The ''truncated cube'' has five special orthogonal projections, centered, on a vertex, on two types of edges, and two types of faces: triangles, and octagons. The last two correspond to the B₂ and A₂ Coxeter planes.

Spherical tiling

The truncated cube can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.

Cartesian coordinates

Cartesian coordinates for the vertices of a truncated hexahedron centered at the origin with edge length 2 are all the permutations of

:(±, ±1, ±1),

where δ_S=+1.

If we let a parameter ''ξ''= , in the case of a Regular Truncated Cube, then the parameter ''ξ'' can be varied between ±1. A value of 1 produces a cube, 0 produces a cuboctahedron, and negative values produces self-intersecting octagrammic faces.
:

If the self-intersected portions of the octagrams are removed, leaving squares, and truncating the triangles into hexagons, truncated octahedra are produced, and the sequence ends with the central squares being reduced to a point, and creating an octahedron.

Dissection

The truncated cube can be dissected into a central cube, with six square cupolae around each of the cube's faces, and 8 regular tetrahedra in the corners. This dissection can also be seen within the runcic cubic honeycomb, with cube, tetrahedron, and rhombicuboctahedron cells.

This dissection can be used to create a Stewart toroid with all regular faces by removing two square cupolae and the central cube. This excavated cube has 16 triangles, 12 squares, and 4 octagons.
:

Vertex arrangement

It shares the vertex arrangement with three nonconvex uniform polyhedra:

Related polyhedra

The truncated cube is related to other polyhedra and tilings in symmetry.

The truncated cube is one of a family of uniform polyhedra related to the cube and regular octahedron.

Symmetry mutations

This polyhedron is topologically related as a part of sequence of uniform truncated polyhedra with vertex configurations (3.2''n''.2''n''), and 'n'',3Coxeter group symmetry, and a series of polyhedra and tilings ''n''.8.8.

Alternated truncation

Truncating alternating vertices of the cube gives the chamfered tetrahedron, i.e. the edge truncation of the tetrahedron.

The truncated triangular trapezohedron is another polyhedron which can be formed from cube edge truncation.

Related polytopes

The '' truncated cube'', is second in a sequence of truncated hypercubes:

Truncated cubical graph

In the mathematical field of graph theory, a truncated cubical graph is the graph of vertices and edges of the ''truncated cube'', one of the Archimedean solids. It has 24 vertices and 36 edges, and is a cubic Archimedean graph.

See also

* Spinning truncated cube
* Cube-connected cycles, a family of graphs that includes the skeleton of the truncated cube
* Chamfered cube, obtained by replacing the edges of a cube with non-uniform hexagons

References

* (Section 3-9)
* Cromwell, P. ''Polyhedra'', CUP hbk (1997), pbk. (1999). Ch.2 p. 79-86 ''Archimedean solids''

External links

*
**
*
Editable printable net of a truncated cube with interactive 3D viewThe Uniform Polyhedra
www.georgehart.com: The Encyclopedia of Polyhedra
** VRMLbr>model


Try: "tC"

{{Polyhedron navigator

Uniform polyhedra
Archimedean solids
Truncated tilings