Thermal Pressure

In thermodynamics, thermal pressure (also known as the thermal pressure coefficient) is a measure of the relative pressure change of a fluid or a solid as a response to a temperature change at constant volume. The concept is related to the Pressure-Temperature Law, also known as Amontons's law or Gay-Lussac's law.

In general pressure, ($P$) can be written as the following sum: $P_\text(V,T) = P_\text(V,T) + \Delta P_\text(V,T)$.

$P_\text$ is the pressure required to compress the material from its volume $V_0$ to volume $V$ at a constant temperature $T_0$. The second term expresses the change in thermal pressure $\Delta P_$ . This is the pressure change at constant volume due to the temperature difference between $T_0$ and $T$. Thus, it is the pressure change along an isochore of the material.

The thermal pressure $\gamma_v$ is customarily expressed in its simple form as $\gamma_v =\left( \frac \right)_.$

Thermodynamic definition

Because of the equivalences between many properties and derivatives within thermodynamics (e.g., see Maxwell Relations), there are many formulations of the thermal pressure coefficient, which are equally valid, leading to distinct yet correct interpretations of its meaning.
Some formulations for the thermal pressure coefficient include:

$\left( \frac \right)_ = \alpha\kappa_T = \fracC_V = \frac$

Where $\alpha$ is the volume thermal expansion, $\kappa_T$ the isothermal bulk modulus, $\gamma$ the Grüneisen parameter, $\beta_T$ the compressibility and $C_V$the constant-volume heat capacity. J.M.Haile (2002). "Lectures in Thermodynamics,Volume1".Macatea Productions, Central, South Carolina, 53-67 177-184.

Details of the calculation:

$\left( \frac \right)_ = -\left( \frac \right)_\left( \frac \right)_ = - (V\alpha) \left(\frac\right) = \alpha\kappa_T$

$\left( \frac \right)_ = \frac = \frac$

The utility of the thermal pressure

The thermal pressure coefficient can be considered as a fundamental property; it is closely related to various properties such as internal pressure, sonic velocity, the entropy of melting, isothermal compressibility, isobaric expansibility, phase transition, etc. Thus, the study of the thermal pressure coefficient provides a useful basis for understanding the nature of liquid and solid. Since it is normally difficult to obtain the properties by thermodynamic and statistical mechanics methods due to complex interactions among molecules, experimental methods attract much attention.
The thermal pressure coefficient is used to calculate results that are applied widely in industry, and they would further accelerate the development of thermodynamic theory.
Commonly the thermal pressure coefficient may be expressed as functions of temperature and volume. There are two main types of calculation of the thermal pressure coefficient: one is the Virial theorem and its derivatives; the other is the Van der Waals type and its derivatives. Gilbert Newton Lewi (1900). "A New Conception of Thermal Pressure and a Theory of Solutions". American Academy of Arts & Sciences. .

Thermal pressure at high temperature

As mentioned above, $\alpha\kappa_T$ is one of the most common formulations for the thermal pressure coefficient.
Both $\alpha$ and $\kappa_T$ are affected by temperature changes, but the value of $\alpha$ and $\kappa_T$ of a solid much less sensitive to temperature change above its Debye temperature. Thus, the thermal pressure of a solid due to moderate temperature change above the Debye temperature can be approximated by assuming a constant value of $\alpha$ and $\kappa_T$. Angel, Ross J., Miozzi Francesca, and Alvaro Matteo (2019). "Limits to the Validity of Thermal-Pressure Equations of State". MDPI.

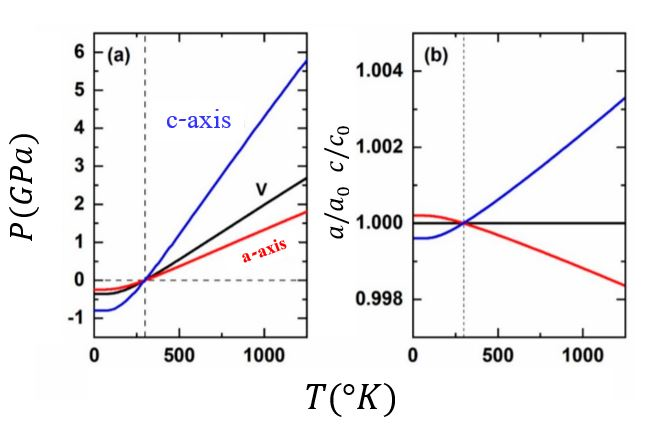
Thermal pressure in a crystal

The thermal pressure of a crystal defines how the unit-cell parameters change as a function of pressure and temperature. Therefore, it also controls how the cell parameters change along an isochore, namely as a function of $\left( \frac \right)_$. Usually, Mie-Grüneisen-Debye and other Quasi harmonic approximation (QHA) based state functions are being used to estimate volumes and densities of mineral phases in diverse applications such as thermodynamic, deep-Earth geophysical models and other planetary bodies. In the case of isotropic (or approximately isotropic) thermal pressure, the unit cell parameter remains constant along the isochore and the QHA is valid. But when the thermal pressure is anisotropic, the unit cell parameter changes so, the frequencies of vibrational modes also change even in constant volume and the QHA is no longer valid.

The combined effect of a change in pressure and temperature is described by the strain tensor $\varepsilon_$:$\varepsilon_= \alpha_ dT- \beta_ dP$

Where $\alpha_$ is the volume thermal expansion tensor and $\beta_$ is the compressibility tensor. The line in the P-T space which indicates that the strain $\epsilon_$ is constant in a particular direction within the crystal is defined as:$\left( \frac \right)_=\frac$

Which is an equivalent definition of the isotropic degree of thermal pressure.

See also

* Isochoric process
* Pressure
* Hydrostatic equilibrium

References

Thermodynamics

{{Improve categories, date=September 2020