Tetrakaidecagon on:
[Wikipedia]
[Google]
[Amazon]
In geometry, a tetradecagon or tetrakaidecagon or 14-gon is a fourteen-sided polygon.
/ref> as shown in the following two examples.
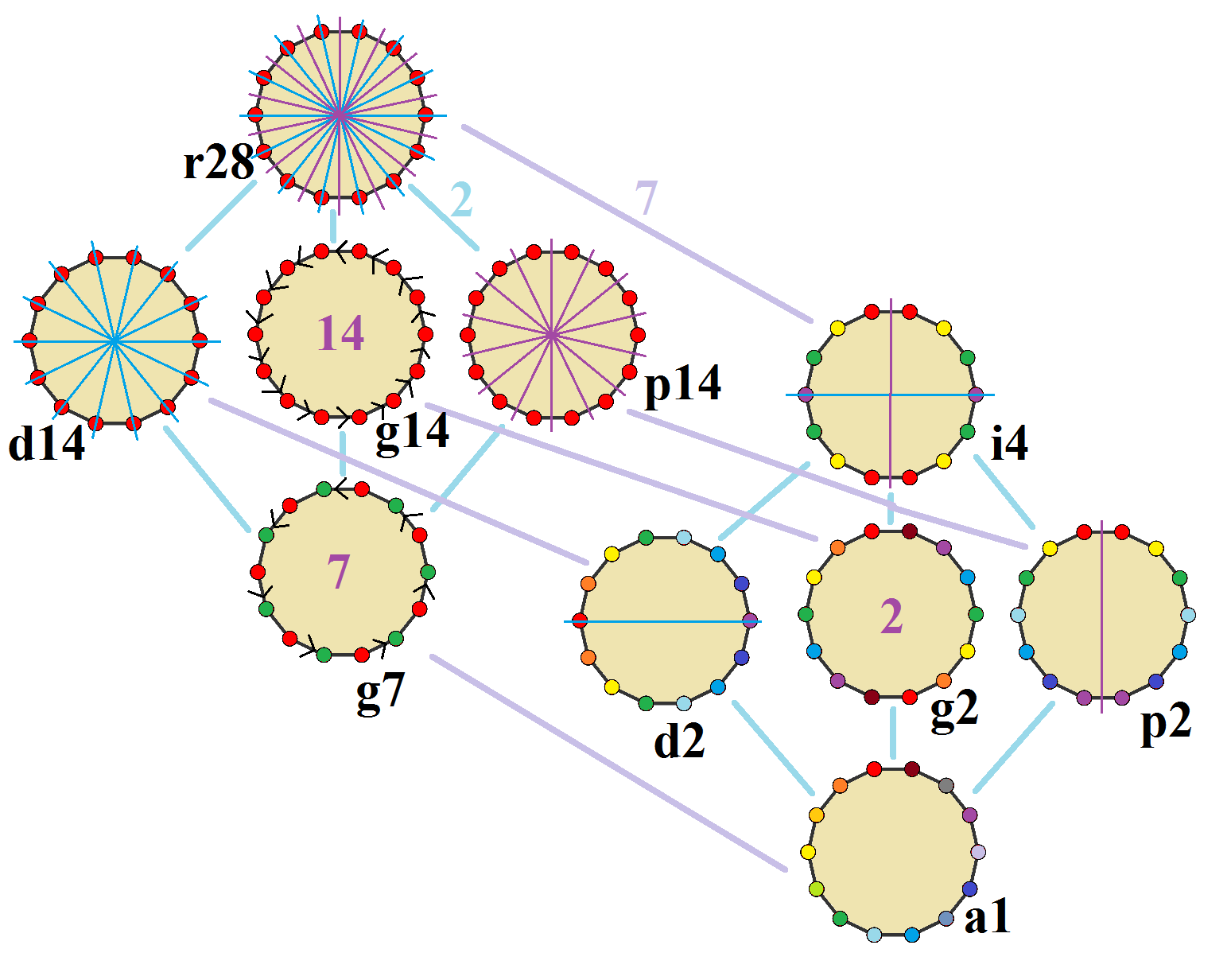 The ''regular tetradecagon'' has Dih14 symmetry, order 28. There are 3 subgroup dihedral symmetries: Dih7, Dih2, and Dih1, and 4 cyclic group symmetries: Z14, Z7, Z2, and Z1.
These 8 symmetries can be seen in 10 distinct symmetries on the tetradecagon, a larger number because the lines of reflections can either pass through vertices or edges. John Conway labels these by a letter and group order. Full symmetry of the regular form is r28 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries in the middle column are labeled as g for their central gyration orders.
Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g14 subgroup has no degrees of freedom but can seen as directed edges.
The highest symmetry irregular tetradecagons are d14, an isogonal tetradecagon constructed by seven mirrors which can alternate long and short edges, and p14, an
The ''regular tetradecagon'' has Dih14 symmetry, order 28. There are 3 subgroup dihedral symmetries: Dih7, Dih2, and Dih1, and 4 cyclic group symmetries: Z14, Z7, Z2, and Z1.
These 8 symmetries can be seen in 10 distinct symmetries on the tetradecagon, a larger number because the lines of reflections can either pass through vertices or edges. John Conway labels these by a letter and group order. Full symmetry of the regular form is r28 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries in the middle column are labeled as g for their central gyration orders.
Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g14 subgroup has no degrees of freedom but can seen as directed edges.
The highest symmetry irregular tetradecagons are d14, an isogonal tetradecagon constructed by seven mirrors which can alternate long and short edges, and p14, an
 A tetradecagram is a 14-sided star polygon, represented by symbol . There are two regular
A tetradecagram is a 14-sided star polygon, represented by symbol . There are two regular
Regular tetradecagon
A ''regular
The term regular can mean normal or in accordance with rules. It may refer to:
People
* Moses Regular (born 1971), America football player
Arts, entertainment, and media Music
* "Regular" (Badfinger song)
* Regular tunings of stringed instrum ...
tetradecagon'' has Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more ...
and can be constructed as a quasiregular truncated heptagon, t, which alternates two types of edges.
The area of a regular
The term regular can mean normal or in accordance with rules. It may refer to:
People
* Moses Regular (born 1971), America football player
Arts, entertainment, and media Music
* "Regular" (Badfinger song)
* Regular tunings of stringed instrum ...
tetradecagon of side length ''a'' is given by
:
Construction
As 14 = 2 × 7, a regular tetradecagon cannot be constructed using acompass and straightedge
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an ideali ...
. However, it is constructible using neusis
In geometry, the neusis (; ; plural: grc, νεύσεις, neuseis, label=none) is a geometric construction method that was used in antiquity by Greek mathematicians.
Geometric construction
The neusis construction consists of fitting a line e ...
with use of the angle trisector, or with a marked ruler,Weisstein, Eric W. "Heptagon." From MathWorld, A Wolfram Web Resource./ref> as shown in the following two examples.

Symmetry
 The ''regular tetradecagon'' has Dih14 symmetry, order 28. There are 3 subgroup dihedral symmetries: Dih7, Dih2, and Dih1, and 4 cyclic group symmetries: Z14, Z7, Z2, and Z1.
These 8 symmetries can be seen in 10 distinct symmetries on the tetradecagon, a larger number because the lines of reflections can either pass through vertices or edges. John Conway labels these by a letter and group order. Full symmetry of the regular form is r28 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries in the middle column are labeled as g for their central gyration orders.
Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g14 subgroup has no degrees of freedom but can seen as directed edges.
The highest symmetry irregular tetradecagons are d14, an isogonal tetradecagon constructed by seven mirrors which can alternate long and short edges, and p14, an
The ''regular tetradecagon'' has Dih14 symmetry, order 28. There are 3 subgroup dihedral symmetries: Dih7, Dih2, and Dih1, and 4 cyclic group symmetries: Z14, Z7, Z2, and Z1.
These 8 symmetries can be seen in 10 distinct symmetries on the tetradecagon, a larger number because the lines of reflections can either pass through vertices or edges. John Conway labels these by a letter and group order. Full symmetry of the regular form is r28 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries in the middle column are labeled as g for their central gyration orders.
Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g14 subgroup has no degrees of freedom but can seen as directed edges.
The highest symmetry irregular tetradecagons are d14, an isogonal tetradecagon constructed by seven mirrors which can alternate long and short edges, and p14, an isotoxal
In geometry, a polytope (for example, a polygon or a polyhedron) or a tiling is isotoxal () or edge-transitive if its symmetries act transitively on its edges. Informally, this means that there is only one type of edge to the object: given two ...
tetradecagon, constructed with equal edge lengths, but vertices alternating two different internal angles. These two forms are duals of each other and have half the symmetry order of the regular tetradecagon.
Dissection
Coxeter states that every zonogon (a 2''m''-gon whose opposite sides are parallel and of equal length) can be dissected into ''m''(''m''-1)/2 parallelograms. In particular this is true for regular polygons with evenly many sides, in which case the parallelograms are all rhombi. For the ''regular tetradecagon'', ''m''=7, and it can be divided into 21: 3 sets of 7 rhombs. This decomposition is based on a Petrie polygon projection of a 7-cube, with 21 of 672 faces. The list defines the number of solutions as 24698, including up to 14-fold rotations and chiral forms in reflection.Numismatic use
The regular tetradecagon is used as the shape of some commemorative gold and silver Malaysian coins, the number of sides representing the 14 states of the Malaysian Federation.Related figures
star polygon
In geometry, a star polygon is a type of non-convex polygon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, certain notable ones can arise through truncation operations ...
s: and , using the same vertices, but connecting every third or fifth points. There are also three compounds: is reduced to 2 as two heptagons, while and are reduced to 2 and 2 as two different heptagrams, and finally is reduced to seven digons.
A notable application of a fourteen-pointed star is in the flag of Malaysia, which incorporates a yellow tetradecagram in the top-right corner, representing the unity of the thirteen states with the federal government
A federation (also known as a federal state) is a political entity characterized by a union of partially self-governing provinces, states, or other regions under a central federal government (federalism). In a federation, the self-governin ...
.
Deeper truncations of the regular heptagon and heptagrams can produce isogonal ( vertex-transitive) intermediate tetradecagram forms with equally spaced vertices and two edge lengths. Other truncations can form double covering polygons 2, namely: t2, t2, and t2.The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), ''Metamorphoses of polygons'', Branko Grünbaum
Isotoxal forms
Anisotoxal polygon
In geometry, a polytope (for example, a polygon or a polyhedron) or a tiling is isotoxal () or edge-transitive if its symmetries act transitively on its edges. Informally, this means that there is only one type of edge to the object: given two ...
can be labeled as with outer most internal angle α, and a star polygon , with ''q'' is a winding number, and gcd(''p'',''q'')=1, ''q''<''p''. Isotoxal tetradecagons have ''p''=7, and since 7 is prime all solutions, q=1..6, are polygons.
Petrie polygons
Regular skew tetradecagons exist as Petrie polygon for many higher-dimensional polytopes, shown in these skew orthogonal projections, including:References
External links
* {{Polygons Polygons by the number of sides