Tautochrone Problem on:
[Wikipedia]
[Google]
[Amazon]
 A tautochrone or isochrone curve (from Greek prefixes tauto- meaning ''same'' or iso- ''equal'', and
A tautochrone or isochrone curve (from Greek prefixes tauto- meaning ''same'' or iso- ''equal'', and
 The tautochrone problem, the attempt to identify this curve, was solved by
The tautochrone problem, the attempt to identify this curve, was solved by 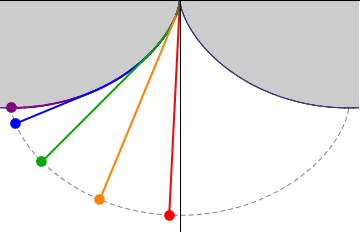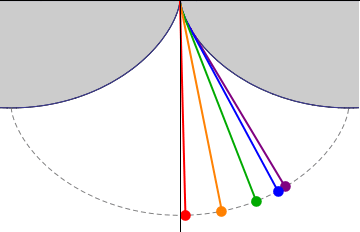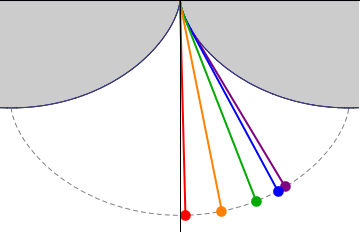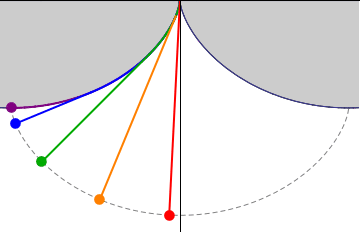 This solution was later used to solve the problem of the
This solution was later used to solve the problem of the 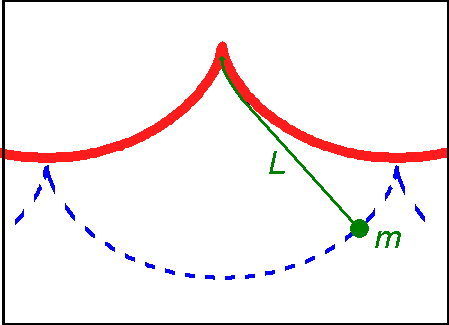 The tautochrone problem was studied by Huygens more closely when it was realized that a pendulum, which follows a circular path, was not
The tautochrone problem was studied by Huygens more closely when it was realized that a pendulum, which follows a circular path, was not
Mathworld
Plane curves Mechanics de:Zykloide#Die Tautochronie der Zykloide
 A tautochrone or isochrone curve (from Greek prefixes tauto- meaning ''same'' or iso- ''equal'', and
A tautochrone or isochrone curve (from Greek prefixes tauto- meaning ''same'' or iso- ''equal'', and chrono
Chrono may refer to:
Prefix
''chrono-'' a Greek combining form relating to time
*chronometry
Chronometry (from Ancient Greek, Greek χρόνος ''chronos'', "time" and μέτρον ''metron'', "measure") is the science of the measurement of t ...
''time'') is the curve for which the time taken by an object sliding without friction in uniform gravity
In physics, gravity () is a fundamental interaction which causes mutual attraction between all things with mass or energy. Gravity is, by far, the weakest of the four fundamental interactions, approximately 1038 times weaker than the str ...
to its lowest point is independent of its starting point on the curve. The curve is a cycloid
In geometry, a cycloid is the curve traced by a point on a circle as it rolls along a straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette, a curve generated by a curve rolling on another ...
, and the time is equal to π times the square root
In mathematics, a square root of a number is a number such that ; in other words, a number whose ''square'' (the result of multiplying the number by itself, or ⋅ ) is . For example, 4 and −4 are square roots of 16, because .
...
of the radius (of the circle which generates the cycloid) over the acceleration of gravity. The tautochrone curve is related to the brachistochrone curve
In physics and mathematics, a brachistochrone curve (), or curve of fastest descent, is the one lying on the plane between a point ''A'' and a lower point ''B'', where ''B'' is not directly below ''A'', on which a bead slides frictionlessly unde ...
, which is also a cycloid
In geometry, a cycloid is the curve traced by a point on a circle as it rolls along a straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette, a curve generated by a curve rolling on another ...
.
The tautochrone problem
 The tautochrone problem, the attempt to identify this curve, was solved by
The tautochrone problem, the attempt to identify this curve, was solved by Christiaan Huygens
Christiaan Huygens, Lord of Zeelhem, ( , , ; also spelled Huyghens; la, Hugenius; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor, who is regarded as one of the greatest scientists ...
in 1659. He proved geometrically in his ''Horologium Oscillatorium
( English: ''The Pendulum Clock: or Geometrical Demonstrations Concerning the Motion of Pendula as Applied to Clocks'') is a book published by Dutch physicist Christiaan Huygens in 1673 and his major work on pendulums and horology. It is regard ...
'', originally published in 1673, that the curve is a cycloid
In geometry, a cycloid is the curve traced by a point on a circle as it rolls along a straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette, a curve generated by a curve rolling on another ...
.
The cycloid is given by a point on a circle of radius tracing a curve as the circle rolls along the axis, as:
Huygens also proved that the time of descent is equal to the time a body takes to fall vertically the same distance as diameter of the circle that generates the cycloid, multiplied by . In modern terms, this means that the time of descent is , where is the radius of the circle which generates the cycloid, and is the gravity of Earth
The gravity of Earth, denoted by , is the net acceleration that is imparted to objects due to the combined effect of gravitation (from mass distribution within Earth) and the centrifugal force (from the Earth's rotation).
It is a vector quan ...
, or more accurately, the earth's gravitational acceleration.
 This solution was later used to solve the problem of the
This solution was later used to solve the problem of the brachistochrone curve
In physics and mathematics, a brachistochrone curve (), or curve of fastest descent, is the one lying on the plane between a point ''A'' and a lower point ''B'', where ''B'' is not directly below ''A'', on which a bead slides frictionlessly unde ...
. Johann Bernoulli
Johann Bernoulli (also known as Jean or John; – 1 January 1748) was a Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family. He is known for his contributions to infinitesimal calculus and educating ...
solved the problem in a paper (''Acta Eruditorum
(from Latin: ''Acts of the Erudite'') was the first scientific journal of the German-speaking lands of Europe, published from 1682 to 1782.
History
''Acta Eruditorum'' was founded in 1682 in Leipzig by Otto Mencke, who became its first editor, ...
'', 1697).
 The tautochrone problem was studied by Huygens more closely when it was realized that a pendulum, which follows a circular path, was not
The tautochrone problem was studied by Huygens more closely when it was realized that a pendulum, which follows a circular path, was not isochronous
A sequence of events is isochronous if the events occur regularly, or at equal time intervals. The term ''isochronous'' is used in several technical contexts, but usually refers to the primary subject maintaining a constant period or interval ...
and thus his pendulum clock
A pendulum clock is a clock that uses a pendulum, a swinging weight, as its timekeeping element. The advantage of a pendulum for timekeeping is that it is a harmonic oscillator: It swings back and forth in a precise time interval dependent on i ...
would keep different time depending on how far the pendulum swung. After determining the correct path, Christiaan Huygens attempted to create pendulum clocks that used a string to suspend the bob and curb cheeks near the top of the string to change the path to the tautochrone curve. These attempts proved unhelpful for a number of reasons. First, the bending of the string causes friction, changing the timing. Second, there were much more significant sources of timing errors that overwhelmed any theoretical improvements that traveling on the tautochrone curve helps. Finally, the "circular error" of a pendulum decreases as length of the swing decreases, so better clock escapement
An escapement is a mechanical linkage in mechanical watches and clocks that gives impulses to the timekeeping element and periodically releases the gear train to move forward, advancing the clock's hands. The impulse action transfers energy to ...
s could greatly reduce this source of inaccuracy.
Later, the mathematicians Joseph Louis Lagrange
Joseph-Louis Lagrange (born Giuseppe Luigi LagrangiaLeonhard Euler
Leonhard Euler ( , ; 15 April 170718 September 1783) was a Swiss mathematician, physicist, astronomer, geographer, logician and engineer who founded the studies of graph theory and topology and made pioneering and influential discoveries in ma ...
provided an analytical solution to the problem.
Lagrangian solution
If the particle's position is parametrized by the arclength from the lowest point, the kinetic energy is proportional to The potential energy is proportional to the height . One way the curve can be an isochrone is if the Lagrangian is that of asimple harmonic oscillator
In mechanics and physics, simple harmonic motion (sometimes abbreviated ) is a special type of periodic motion of a body resulting from a dynamic equilibrium between an inertial force, proportional to the acceleration of the body away from the ...
: the height of the curve must be proportional to the arclength squared.
where the constant of proportionality has been set to 1 by changing units of length.
The differential form of this relation is
which eliminates , and leaves a differential equation for and . To find the solution, integrate for in terms of :
where . This integral is the area under a circle, which can be naturally cut into a triangle and a circular wedge:
To see that this is a strangely parametrized cycloid
In geometry, a cycloid is the curve traced by a point on a circle as it rolls along a straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette, a curve generated by a curve rolling on another ...
, change variables to disentangle the transcendental and algebraic parts by defining the angle . This yields
which is the standard parametrization, except for the scale of and .
"Virtual gravity" solution
The simplest solution to the tautochrone problem is to note a direct relation between the angle of an incline and the gravity felt by a particle on the incline. A particle on a 90° vertical incline undergoes full gravitational acceleration , while a particle on a horizontal plane undergoes zero gravitational acceleration. At intermediate angles, the acceleration due to "virtual gravity" by the particle is . Note that is measured between the tangent to the curve and the horizontal, with angles above the horizontal being treated as positive angles. Thus, varies from to . The position of a mass measured along a tautochrone curve, , must obey the following differential equation: which, along with the initial conditions and , has solution: It can be easily verified both that this solution solves the differential equation and that a particle will reach at time from any starting position . The problem is now to construct a curve that will cause the mass to obey the above motion.Newton's second law
Newton's laws of motion are three basic Scientific law, laws of classical mechanics that describe the relationship between the motion of an object and the forces acting on it. These laws can be paraphrased as follows:
# A body remains at re ...
shows that the force of gravity and the acceleration of the mass are related by:
The explicit appearance of the distance, , is troublesome, but we can differentiate to obtain a more manageable form:
This equation relates the change in the curve's angle to the change in the distance along the curve. We now use trigonometry
Trigonometry () is a branch of mathematics that studies relationships between side lengths and angles of triangles. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. ...
to relate the angle to the differential lengths , and :
Replacing with in the above equation lets us solve for in terms of :
Likewise, we can also express in terms of and solve for in terms of :
Substituting and , we see that these parametric equations
Parametric may refer to:
Mathematics
*Parametric equation, a representation of a curve through equations, as functions of a variable
* Parametric statistics, a branch of statistics that assumes data has come from a type of probability distribu ...
for and are those of a point on a circle of radius rolling along a horizontal line (a cycloid
In geometry, a cycloid is the curve traced by a point on a circle as it rolls along a straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette, a curve generated by a curve rolling on another ...
), with the circle center at the coordinates :
Note that ranges from . It is typical to set and so that the lowest point on the curve coincides with the origin. Therefore:
Solving for and remembering that is the time required for descent, being a quarter of a whole cycle, we find the descent time in terms of the radius :
(Based loosely on ''Proctor'', pp. 135–139)
Abel's solution
Niels Henrik Abel
Niels Henrik Abel ( , ; 5 August 1802 – 6 April 1829) was a Norwegian mathematician who made pioneering contributions in a variety of fields. His most famous single result is the first complete proof demonstrating the impossibility of solvin ...
attacked a generalized version of the tautochrone problem (''Abel's mechanical problem''), namely, given a function that specifies the total time of descent for a given starting height, find an equation of the curve that yields this result. The tautochrone problem is a special case of Abel's mechanical problem when is a constant.
Abel's solution begins with the principle of conservation of energy
In physics and chemistry, the law of conservation of energy states that the total energy of an isolated system remains constant; it is said to be ''conserved'' over time. This law, first proposed and tested by Émilie du Châtelet, means tha ...
– since the particle is frictionless, and thus loses no energy to heat
In thermodynamics, heat is defined as the form of energy crossing the boundary of a thermodynamic system by virtue of a temperature difference across the boundary. A thermodynamic system does not ''contain'' heat. Nevertheless, the term is ...
, its kinetic energy
In physics, the kinetic energy of an object is the energy that it possesses due to its motion.
It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its a ...
at any point is exactly equal to the difference in gravitational potential energy
Gravitational energy or gravitational potential energy is the potential energy a massive object has in relation to another massive object due to gravity. It is the potential energy associated with the gravitational field, which is released (conv ...
from its starting point. The kinetic energy is , and since the particle is constrained to move along a curve, its velocity is simply , where is the distance measured along the curve. Likewise, the gravitational potential energy gained in falling from an initial height to a height is , thus:
In the last equation, we have anticipated writing the distance remaining along the curve as a function of height (, recognized that the distance remaining must decrease as time increases (thus the minus sign), and used the chain rule
In calculus, the chain rule is a formula that expresses the derivative of the Function composition, composition of two differentiable functions and in terms of the derivatives of and . More precisely, if h=f\circ g is the function such that h(x) ...
in the form .
Now we integrate from to to get the total time required for the particle to fall:
This is called Abel's integral equation and allows us to compute the total time required for a particle to fall along a given curve (for which would be easy to calculate). But Abel's mechanical problem requires the converse – given , we wish to find , from which an equation for the curve would follow in a straightforward manner. To proceed, we note that the integral on the right is the convolution
In mathematics (in particular, functional analysis), convolution is a mathematical operation on two functions ( and ) that produces a third function (f*g) that expresses how the shape of one is modified by the other. The term ''convolution' ...
of with and thus take the Laplace transform
In mathematics, the Laplace transform, named after its discoverer Pierre-Simon Laplace (), is an integral transform that converts a function of a real variable (usually t, in the ''time domain'') to a function of a complex variable s (in the ...
of both sides with respect to variable :
where . Since , we now have an expression for the Laplace transform of in terms of the Laplace transform of :
This is as far as we can go without specifying . Once is known, we can compute its Laplace transform, calculate the Laplace transform of and then take the inverse transform (or try to) to find .
For the tautochrone problem, is constant. Since the Laplace transform of 1 is , i.e., , we find the shape function :
Making use again of the Laplace transform above, we invert the transform and conclude:
It can be shown that the cycloid obeys this equation. It needs one step further to do the integral with respect to to obtain the expression of the path shape.
(''Simmons'', Section 54).
See also
*Beltrami identity Beltrami may refer to:
Places in the United States
*Beltrami County, Minnesota
*Beltrami, Minnesota
* Beltrami, Minneapolis, a neighborhood in Minneapolis, Minnesota
Other uses
*Beltrami (surname) Beltrami is an Italian surname. Notable people wit ...
* Brachistochrone curve
In physics and mathematics, a brachistochrone curve (), or curve of fastest descent, is the one lying on the plane between a point ''A'' and a lower point ''B'', where ''B'' is not directly below ''A'', on which a bead slides frictionlessly unde ...
* Calculus of variations
The calculus of variations (or Variational Calculus) is a field of mathematical analysis that uses variations, which are small changes in functions
and functionals, to find maxima and minima of functionals: mappings from a set of functions t ...
* Catenary
In physics and geometry, a catenary (, ) is the curve that an idealized hanging chain or cable assumes under its own weight when supported only at its ends in a uniform gravitational field.
The catenary curve has a U-like shape, superficia ...
* Cycloid
In geometry, a cycloid is the curve traced by a point on a circle as it rolls along a straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette, a curve generated by a curve rolling on another ...
* Uniformly accelerated motion
References
Bibliography
* * {{cite book , url=https://books.google.com/books?id=6UIZBvs0diIC , title=A Treatise on the Cycloid and All Forms of Cycloidal Curves, and on the Use of Such Curves in Dealing with the Motions of Planets, Comets, etc., and of Matter Projected from the Sun , last1=Proctor , first1=Richard Anthony , year=1878External links
Mathworld
Plane curves Mechanics de:Zykloide#Die Tautochronie der Zykloide