Symmetrization methods on:
[Wikipedia]
[Google]
[Amazon]
In mathematics the symmetrization methods are algorithms of transforming a set to a ball with equal volume and centered at the origin. ''B'' is called the symmetrized version of ''A'', usually denoted . These algorithms show up in solving the classical
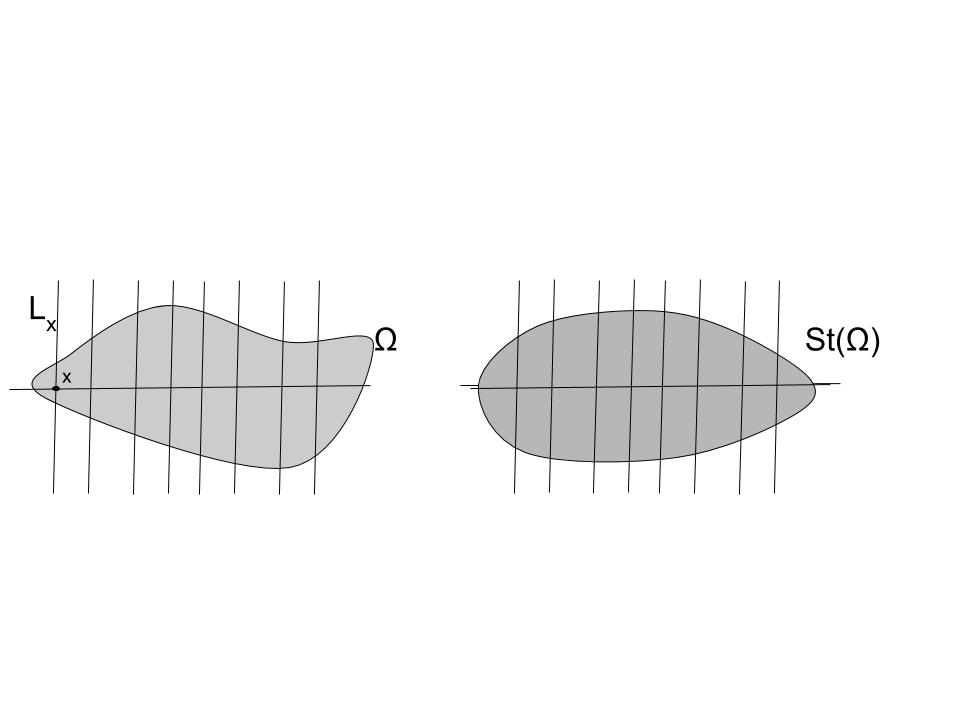 Steiner symmetrization was introduced by Steiner (1838) to solve the isoperimetric theorem stated above. Let be a
Steiner symmetrization was introduced by Steiner (1838) to solve the isoperimetric theorem stated above. Let be a
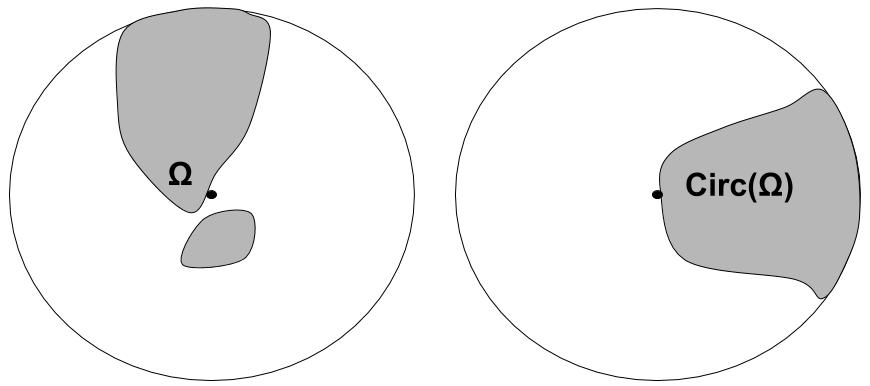 A popular method for symmetrization in the plane is Polya's circular symmetrization. After, its generalization will be described to higher dimensions. Let be a domain; then its circular symmetrization with regard to the positive real axis is defined as follows: Let
i.e. contain the arcs of radius t contained in . So it is defined
* If is the full circle, then .
* If the length is , then .
* iff .
In higher dimensions , its spherical symmetrization wrt to positive axis of is defined as follows: Let
i.e. contain the caps of radius r contained in . Also, for the first coordinate let if . So as above
* If is the full cap, then .
* If the surface area is , then where is picked so that its surface area is . In words, is a cap symmetric around the positive axis with the same area as the intersection .
* iff .
A popular method for symmetrization in the plane is Polya's circular symmetrization. After, its generalization will be described to higher dimensions. Let be a domain; then its circular symmetrization with regard to the positive real axis is defined as follows: Let
i.e. contain the arcs of radius t contained in . So it is defined
* If is the full circle, then .
* If the length is , then .
* iff .
In higher dimensions , its spherical symmetrization wrt to positive axis of is defined as follows: Let
i.e. contain the caps of radius r contained in . Also, for the first coordinate let if . So as above
* If is the full cap, then .
* If the surface area is , then where is picked so that its surface area is . In words, is a cap symmetric around the positive axis with the same area as the intersection .
* iff .
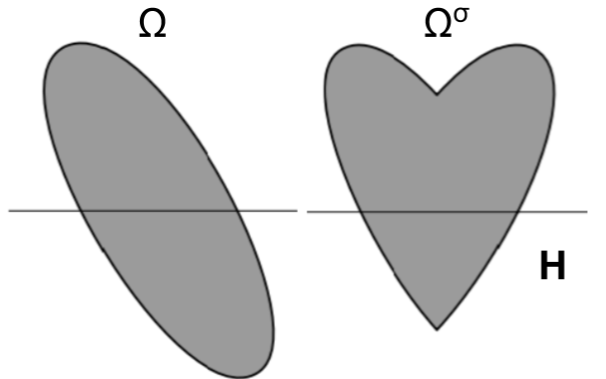 Let be a domain and be a hyperplane through the origin. Denote the reflection across that plane to the positive halfspace as or just when it is clear from the context. Also, the reflected across hyperplane H is defined as . Then, the polarized is denoted as and defined as follows
* If , then .
* If , then .
* If , then .
In words, is simply reflected to the halfspace . It turns out that this transformation can approximate the above ones (in the
Let be a domain and be a hyperplane through the origin. Denote the reflection across that plane to the positive halfspace as or just when it is clear from the context. Also, the reflected across hyperplane H is defined as . Then, the polarized is denoted as and defined as follows
* If , then .
* If , then .
* If , then .
In words, is simply reflected to the halfspace . It turns out that this transformation can approximate the above ones (in the
isoperimetric inequality
In mathematics, the isoperimetric inequality is a geometric inequality involving the perimeter of a set and its volume. In n-dimensional space \R^n the inequality lower bounds the surface area or perimeter \operatorname(S) of a set S\subset\R^n ...
problem, which asks: Given all two-dimensional shapes of a given area, which of them has the minimal perimeter
A perimeter is a closed path that encompasses, surrounds, or outlines either a two dimensional shape or a one-dimensional length. The perimeter of a circle or an ellipse is called its circumference.
Calculating the perimeter has several pr ...
(for details see Isoperimetric inequality
In mathematics, the isoperimetric inequality is a geometric inequality involving the perimeter of a set and its volume. In n-dimensional space \R^n the inequality lower bounds the surface area or perimeter \operatorname(S) of a set S\subset\R^n ...
). The conjectured answer was the disk and Steiner in 1838 showed this to be true using the Steiner symmetrization method (described below). From this many other isoperimetric problems sprung and other symmetrization algorithms. For example, Rayleigh's conjecture is that the first eigenvalue
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denot ...
of the Dirichlet problem
In mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation (PDE) in the interior of a given region that takes prescribed values on the boundary of the region.
The Dirichlet pro ...
is minimized for the ball (see Rayleigh–Faber–Krahn inequality In spectral geometry, the Rayleigh–Faber–Krahn inequality, named after its conjecturer, Lord Rayleigh, and two individuals who independently proved the conjecture, G. Faber and Edgar Krahn, is an inequality concerning the lowest Dirichlet eig ...
for details). Another problem is that the Newtonian capacity of a set In mathematics, the capacity of a set in Euclidean space is a measure of the "size" of that set. Unlike, say, Lebesgue measure, which measures a set's volume or physical extent, capacity is a mathematical analogue of a set's ability to hold electri ...
A is minimized by and this was proved by Polya and G. Szego (1951) using circular symmetrization (described below).
Symmetrization
If is measurable, then it is denoted by the symmetrized version of i.e. a ball such that . We denote by the symmetric decreasing rearrangement of nonnegative measurable function f and define it as , where is the symmetrized version of preimage set . The methods described below have been proved to transform to i.e. given a sequence of symmetrization transformations there is , where is theHausdorff distance In mathematics, the Hausdorff distance, or Hausdorff metric, also called Pompeiu–Hausdorff distance, measures how far two subsets of a metric space are from each other. It turns the set of non-empty compact subsets of a metric space into a metri ...
(for discussion and proofs see )
Steiner symmetrization
 Steiner symmetrization was introduced by Steiner (1838) to solve the isoperimetric theorem stated above. Let be a
Steiner symmetrization was introduced by Steiner (1838) to solve the isoperimetric theorem stated above. Let be a hyperplane
In geometry, a hyperplane is a subspace whose dimension is one less than that of its '' ambient space''. For example, if a space is 3-dimensional then its hyperplanes are the 2-dimensional planes, while if the space is 2-dimensional, its hype ...
through the origin. Rotate space so that is the ( is the ''n''th coordinate in ) hyperplane. For each let the perpendicular line through be . Then by replacing each by a line centered at H and with length we obtain the Steiner symmetrized version.
:
It is denoted by the Steiner symmetrization wrt to hyperplane of nonnegative measurable function and for fixed define it as
:
Properties
* It preserves convexity: if is convex, then is also convex. *It is linear: . *Super-additive: .Circular symmetrization
 A popular method for symmetrization in the plane is Polya's circular symmetrization. After, its generalization will be described to higher dimensions. Let be a domain; then its circular symmetrization with regard to the positive real axis is defined as follows: Let
i.e. contain the arcs of radius t contained in . So it is defined
* If is the full circle, then .
* If the length is , then .
* iff .
In higher dimensions , its spherical symmetrization wrt to positive axis of is defined as follows: Let
i.e. contain the caps of radius r contained in . Also, for the first coordinate let if . So as above
* If is the full cap, then .
* If the surface area is , then where is picked so that its surface area is . In words, is a cap symmetric around the positive axis with the same area as the intersection .
* iff .
A popular method for symmetrization in the plane is Polya's circular symmetrization. After, its generalization will be described to higher dimensions. Let be a domain; then its circular symmetrization with regard to the positive real axis is defined as follows: Let
i.e. contain the arcs of radius t contained in . So it is defined
* If is the full circle, then .
* If the length is , then .
* iff .
In higher dimensions , its spherical symmetrization wrt to positive axis of is defined as follows: Let
i.e. contain the caps of radius r contained in . Also, for the first coordinate let if . So as above
* If is the full cap, then .
* If the surface area is , then where is picked so that its surface area is . In words, is a cap symmetric around the positive axis with the same area as the intersection .
* iff .
Polarization
 Let be a domain and be a hyperplane through the origin. Denote the reflection across that plane to the positive halfspace as or just when it is clear from the context. Also, the reflected across hyperplane H is defined as . Then, the polarized is denoted as and defined as follows
* If , then .
* If , then .
* If , then .
In words, is simply reflected to the halfspace . It turns out that this transformation can approximate the above ones (in the
Let be a domain and be a hyperplane through the origin. Denote the reflection across that plane to the positive halfspace as or just when it is clear from the context. Also, the reflected across hyperplane H is defined as . Then, the polarized is denoted as and defined as follows
* If , then .
* If , then .
* If , then .
In words, is simply reflected to the halfspace . It turns out that this transformation can approximate the above ones (in the Hausdorff distance In mathematics, the Hausdorff distance, or Hausdorff metric, also called Pompeiu–Hausdorff distance, measures how far two subsets of a metric space are from each other. It turns the set of non-empty compact subsets of a metric space into a metri ...
) (see ).
References
* * * *{{Cite web , last = Morgan , first = Frank , title = Symmetrization , year = 2009 , url=http://math.williams.edu/symmmetrization/ , ref=Mor09 , access-date = 1 November 2015 Geometric inequalities Geometric algorithms