surjective homomorphism

In algebra, a homomorphism is a structure-preserving map between two algebraic structures of the same type (such as two groups, two rings, or two vector spaces). The word ''homomorphism'' comes from the Ancient Greek language: () meaning "same" and () meaning "form" or "shape". However, the word was apparently introduced to mathematics due to a (mis)translation of German meaning "similar" to meaning "same". The term "homomorphism" appeared as early as 1892, when it was attributed to the German mathematician Felix Klein (1849–1925).

Homomorphisms of vector spaces are also called linear maps, and their study is the subject of linear algebra.

The concept of homomorphism has been generalized, under the name of morphism, to many other structures that either do not have an underlying set, or are not algebraic. This generalization is the starting point of category theory.

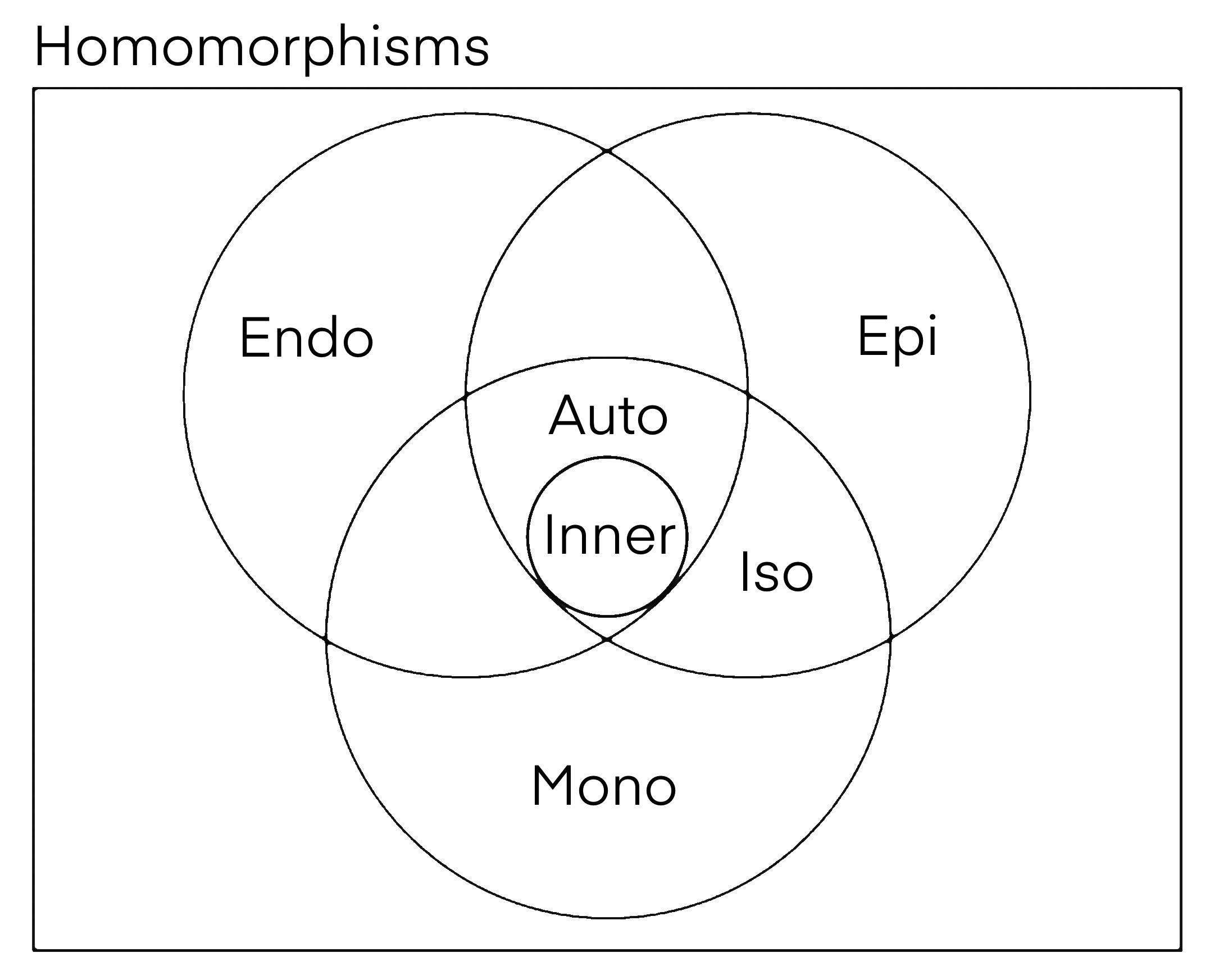
A homomorphism may also be an isomorphism, an endomorphism, an automorphism, etc. (see below). Each of those can be defined in a way that may be generalized to any class of morphisms.

Definition

A homomorphism is a map between two algebraic structures of the same type (that is of the same name), that preserves the operations of the structures. This means a map $f: A \to B$ between two sets $A$, $B$ equipped with the same structure such that, if $\cdot$ is an operation of the structure (supposed here, for simplification, to be a binary operation), then
:$f(x\cdot y)=f(x)\cdot f(y)$
for every pair $x$, $y$ of elements of $A$.As it is often the case, but not always, the same symbol for the operation of both $A$ and $B$ was used here. One says often that $f$ preserves the operation or is compatible with the operation.

Formally, a map $f: A\to B$ preserves an operation $\mu$ of arity ''k'', defined on both $A$ and $B$ if
:$f(\mu_A(a_1, \ldots, a_k)) = \mu_B(f(a_1), \ldots, f(a_k)),$
for all elements $a_1, ..., a_k$ in $A$.

The operations that must be preserved by a homomorphism include 0-ary operations, that is the constants. In particular, when an identity element is required by the type of structure, the identity element of the first structure must be mapped to the corresponding identity element of the second structure.

For example:

* A semigroup homomorphism is a map between semigroups that preserves the semigroup operation.
* A monoid homomorphism is a map between monoids that preserves the monoid operation and maps the identity element of the first monoid to that of the second monoid (the identity element is a 0-ary operation).
* A group homomorphism is a map between groups that preserves the group operation. This implies that the group homomorphism maps the identity element of the first group to the identity element of the second group, and maps the inverse of an element of the first group to the inverse of the image of this element. Thus a semigroup homomorphism between groups is necessarily a group homomorphism.
* A ring homomorphism is a map between rings that preserves the ring addition, the ring multiplication, and the multiplicative identity. Whether the multiplicative identity is to be preserved depends upon the definition of ''ring'' in use. If the multiplicative identity is not preserved, one has a rng homomorphism.
* A linear map is a homomorphism of vector spaces; that is, a group homomorphism between vector spaces that preserves the abelian group structure and scalar multiplication.
* A module homomorphism, also called a linear map between modules, is defined similarly.
* An algebra homomorphism is a map that preserves the algebra operations.

An algebraic structure may have more than one operation, and a homomorphism is required to preserve each operation. Thus a map that preserves only some of the operations is not a homomorphism of the structure, but only a homomorphism of the substructure obtained by considering only the preserved operations. For example, a map between monoids that preserves the monoid operation and not the identity element, is not a monoid homomorphism, but only a semigroup homomorphism.

The notation for the operations does not need to be the same in the source and the target of a homomorphism. For example, the real numbers form a group for addition, and the positive real numbers form a group for multiplication. The exponential function
:$x\mapsto e^x$
satisfies
:$e^ = e^xe^y,$
and is thus a homomorphism between these two groups. It is even an isomorphism (see below), as its inverse function, the natural logarithm, satisfies
:$\ln(xy)=\ln(x)+\ln(y),$
and is also a group homomorphism.

Examples

The real numbers are a ring, having both addition and multiplication. The set of all 2×2 matrices is also a ring, under matrix addition and matrix multiplication. If we define a function between these rings as follows:
:$f(r) = \begin r & 0 \\ 0 & r \end$
where is a real number, then is a homomorphism of rings, since preserves both addition:
:$f(r+s) = \begin r+s & 0 \\ 0 & r+s \end = \begin r & 0 \\ 0 & r \end + \begin s & 0 \\ 0 & s \end = f(r) + f(s)$
and multiplication:
:$f(rs) = \begin rs & 0 \\ 0 & rs \end = \begin r & 0 \\ 0 & r \end \begin s & 0 \\ 0 & s \end = f(r)\,f(s).$

For another example, the nonzero complex numbers form a group under the operation of multiplication, as do the nonzero real numbers. (Zero must be excluded from both groups since it does not have a multiplicative inverse, which is required for elements of a group.) Define a function $f$ from the nonzero complex numbers to the nonzero real numbers by
:$f(z) = , z, .$
That is, $f$ is the absolute value (or modulus) of the complex number $z$. Then $f$ is a homomorphism of groups, since it preserves multiplication:
:$f(z_1 z_2) = , z_1 z_2, = , z_1, , z_2, = f(z_1) f(z_2).$
Note that cannot be extended to a homomorphism of rings (from the complex numbers to the real numbers), since it does not preserve addition:
:$, z_1 + z_2, \ne , z_1, + , z_2, .$

As another example, the diagram shows a monoid homomorphism $f$ from the monoid $(\mathbb, +, 0)$ to the monoid $(\mathbb, \times, 1)$. Due to the different names of corresponding operations, the structure preservation properties satisfied by $f$ amount to $f(x+y) = f(x) \times f(y)$ and $f(0) = 1$.

A composition algebra $A$ over a field $F$ has a quadratic form, called a ''norm'', $N: A \to F$, which is a group homomorphism from the multiplicative group of $A$ to the multiplicative group of $F$.

Special homomorphisms

Several kinds of homomorphisms have a specific name, which is also defined for general morphisms.

Isomorphism

An isomorphism between algebraic structures of the same type is commonly defined as a bijective homomorphism.

In the more general context of category theory, an isomorphism is defined as a morphism that has an inverse that is also a morphism. In the specific case of algebraic structures, the two definitions are equivalent, although they may differ for non-algebraic structures, which have an underlying set.

More precisely, if
:$f: A\to B$
is a (homo)morphism, it has an inverse if there exists a homomorphism
:$g: B\to A$
such that
:$f\circ g = \operatorname_B \qquad \text \qquad g\circ f = \operatorname_A.$

If $A$ and $B$ have underlying sets, and $f: A \to B$ has an inverse $g$, then $f$ is bijective. In fact, $f$ is injective, as $f(x) = f(y)$ implies $x = g(f(x)) = g(f(y)) = y$, and $f$ is surjective, as, for any $x$ in $B$, one has $x = f(g(x))$, and $x$ is the image of an element of $A$.

Conversely, if $f: A \to B$ is a bijective homomorphism between algebraic structures, let $g: B \to A$ be the map such that $g(y)$ is the unique element $x$ of $A$ such that $f(x) = y$. One has $f \circ g = \operatorname_B \text g \circ f = \operatorname_A,$ and it remains only to show that is a homomorphism. If $*$ is a binary operation of the structure, for every pair $x$, $y$ of elements of $B$, one has
:$g(x*_B y) = g(f(g(x))*_Bf(g(y))) = g(f(g(x)*_A g(y))) = g(x)*_A g(y),$
and $g$ is thus compatible with $*.$ As the proof is similar for any arity, this shows that $g$ is a homomorphism.

This proof does not work for non-algebraic structures. For examples, for topological spaces, a morphism is a continuous map, and the inverse of a bijective continuous map is not necessarily continuous. An isomorphism of topological spaces, called homeomorphism or bicontinuous map, is thus a bijective continuous map, whose inverse is also continuous.

Endomorphism

An endomorphism is a homomorphism whose domain equals the codomain, or, more generally, a morphism whose source is equal to its target.

The endomorphisms of an algebraic structure, or of an object of a category form a monoid under composition.

The endomorphisms of a vector space or of a module form a ring. In the case of a vector space or a free module of finite dimension, the choice of a basis induces a ring isomorphism between the ring of endomorphisms and the ring of square matrices of the same dimension.

Automorphism

An automorphism is an endomorphism that is also an isomorphism.

The automorphisms of an algebraic structure or of an object of a category form a group under composition, which is called the automorphism group of the structure.

Many groups that have received a name are automorphism groups of some algebraic structure. For example, the general linear group $\operatorname_n(k)$ is the automorphism group of a vector space of dimension $n$ over a field $k$.

The automorphism groups of fields were introduced by Évariste Galois for studying the roots of polynomials, and are the basis of Galois theory.

Monomorphism

For algebraic structures, monomorphisms are commonly defined as injective homomorphisms.

In the more general context of category theory, a monomorphism is defined as a morphism that is left cancelable. This means that a (homo)morphism $f:A \to B$ is a monomorphism if, for any pair $g$, $h$ of morphisms from any other object $C$ to $A$, then $f \circ g = f \circ h$ implies $g = h$.

These two definitions of ''monomorphism'' are equivalent for all common algebraic structures. More precisely, they are equivalent for fields, for which every homomorphism is a monomorphism, and for varieties of universal algebra, that is algebraic structures for which operations and axioms (identities) are defined without any restriction (the fields do not form a variety, as the multiplicative inverse is defined either as a unary operation or as a property of the multiplication, which are, in both cases, defined only for nonzero elements).

In particular, the two definitions of a monomorphism are equivalent for sets, magmas, semigroups, monoids, groups, rings, fields, vector spaces and modules.

A split monomorphism is a homomorphism that has a left inverse and thus it is itself a right inverse of that other homomorphism. That is, a homomorphism $f\colon A \to B$ is a split monomorphism if there exists a homomorphism $g\colon B \to A$ such that $g \circ f = \operatorname_A.$ A split monomorphism is always a monomorphism, for both meanings of ''monomorphism''. For sets and vector spaces, every monomorphism is a split monomorphism, but this property does not hold for most common algebraic structures.

''An injective homomorphism is left cancelable'': If $f\circ g = f\circ h,$ one has $f(g(x))=f(h(x))$ for every $x$ in $C$, the common source of $g$ and $h$. If $f$ is injective, then $g(x) = h(x)$, and thus $g = h$. This proof works not only for algebraic structures, but also for any category whose objects are sets and arrows are maps between these sets. For example, an injective continuous map is a monomorphism in the category of topological spaces.

For proving that, conversely, a left cancelable homomorphism is injective, it is useful to consider a ''free object on $x$''. Given a variety of algebraic structures a free object on $x$ is a pair consisting of an algebraic structure $L$ of this variety and an element $x$ of $L$ satisfying the following universal property: for every structure $S$ of the variety, and every element $s$ of $S$, there is a unique homomorphism $f: L\to S$ such that $f(x) = s$. For example, for sets, the free object on $x$ is simply $\$; for semigroups, the free object on $x$ is $\,$ which, as, a semigroup, is isomorphic to the additive semigroup of the positive integers; for monoids, the free object on $x$ is $\,$ which, as, a monoid, is isomorphic to the additive monoid of the nonnegative integers; for groups, the free object on $x$ is the infinite cyclic group $\,$ which, as, a group, is isomorphic to the additive group of the integers; for rings, the free object on $x$ is the polynomial ring \mathbb for vector spaces or modules, the free object on $x$ is the vector space or free module that has $x$ as a basis.

''If a free object over $x$ exists, then every left cancelable homomorphism is injective'': let $f\colon A \to B$ be a left cancelable homomorphism, and $a$ and $b$ be two elements of $A$ such $f(a) = f(b)$. By definition of the free object $F$, there exist homomorphisms $g$ and $h$ from $F$ to $A$ such that $g(x) = a$ and $h(x) = b$. As $f(g(x)) = f(h(x))$, one has $f \circ g = f \circ h,$ by the uniqueness in the definition of a universal property. As $f$ is left cancelable, one has $g = h$, and thus $a = b$. Therefore, $f$ is injective.

''Existence of a free object on $x$ for a variety'' (see also ): For building a free object over $x$, consider the set $W$ of the well-formed formulas built up from $x$ and the operations of the structure. Two such formulas are said equivalent if one may pass from one to the other by applying the axioms ( identities of the structure). This defines an equivalence relation, if the identities are not subject to conditions, that is if one works with a variety. Then the operations of the variety are well defined on the set of equivalence classes of $W$ for this relation. It is straightforward to show that the resulting object is a free object on $x$.

Epimorphism

In algebra, epimorphisms are often defined as surjective homomorphisms. On the other hand, in category theory, epimorphisms are defined as right cancelable morphisms. This means that a (homo)morphism $f: A \to B$ is an epimorphism if, for any pair $g$, $h$ of morphisms from $B$ to any other object $C$, the equality $g \circ f = h \circ f$ implies $g = h$.

A surjective homomorphism is always right cancelable, but the converse is not always true for algebraic structures. However, the two definitions of ''epimorphism'' are equivalent for sets, vector spaces, abelian groups, modules (see below for a proof), and groups. The importance of these structures in all mathematics, and specially in linear algebra and homological algebra, may explain the coexistence of two non-equivalent definitions.

Algebraic structures for which there exist non-surjective epimorphisms include semigroups and rings. The most basic example is the inclusion of integers into rational numbers, which is a homomorphism of rings and of multiplicative semigroups. For both structures it is a monomorphism and a non-surjective epimorphism, but not an isomorphism.

A wide generalization of this example is the localization of a ring by a multiplicative set. Every localization is a ring epimorphism, which is not, in general, surjective. As localizations are fundamental in commutative algebra and algebraic geometry, this may explain why in these areas, the definition of epimorphisms as right cancelable homomorphisms is generally preferred.

A split epimorphism is a homomorphism that has a right inverse and thus it is itself a left inverse of that other homomorphism. That is, a homomorphism $f\colon A \to B$ is a split epimorphism if there exists a homomorphism $g\colon B \to A$ such that $f\circ g = \operatorname_B.$ A split epimorphism is always an epimorphism, for both meanings of ''epimorphism''. For sets and vector spaces, every epimorphism is a split epimorphism, but this property does not hold for most common algebraic structures.

In summary, one has
:$\text \implies \text\implies \text ;$
the last implication is an equivalence for sets, vector spaces, modules and abelian groups; the first implication is an equivalence for sets and vector spaces.

Let $f\colon A \to B$ be a homomorphism. We want to prove that if it is not surjective, it is not right cancelable.

In the case of sets, let $b$ be an element of $B$ that not belongs to $f(A)$, and define $g, h\colon B \to B$ such that $g$ is the identity function, and that $h(x) = x$ for every $x \in B,$ except that $h(b)$ is any other element of $B$. Clearly $f$ is not right cancelable, as $g \neq h$ and $g \circ f = h \circ f.$

In the case of vector spaces, abelian groups and modules, the proof relies on the existence of cokernels and on the fact that the zero maps are homomorphisms: let $C$ be the cokernel of $f$, and $g\colon B \to C$ be the canonical map, such that $g(f(A)) = 0$. Let $h\colon B\to C$ be the zero map. If $f$ is not surjective, $C \neq 0$, and thus $g \neq h$ (one is a zero map, while the other is not). Thus $f$ is not cancelable, as $g \circ f = h \circ f$ (both are the zero map from $A$ to $C$).

Kernel

Any homomorphism $f: X \to Y$ defines an equivalence relation $\sim$ on $X$ by $a \sim b$ if and only if $f(a) = f(b)$. The relation $\sim$ is called the kernel of $f$. It is a congruence relation on $X$. The quotient set $X/$ can then be given a structure of the same type as $X$, in a natural way, by defining the operations of the quotient set by \ast = \ast y/math>, for each operation $\ast$ of $X$. In that case the image of $X$ in $Y$ under the homomorphism $f$ is necessarily isomorphic to $X/\!\sim$; this fact is one of the isomorphism theorems.

When the algebraic structure is a group for some operation, the equivalence class $K$ of the identity element of this operation suffices to characterize the equivalence relation. In this case, the quotient by the equivalence relation is denoted by $X/K$ (usually read as "$X$ mod $K$"). Also in this case, it is $K$, rather than $\sim$, that is called the kernel of $f$. The kernels of homomorphisms of a given type of algebraic structure are naturally equipped with some structure. This structure type of the kernels is the same as the considered structure, in the case of abelian groups, vector spaces and modules, but is different and has received a specific name in other cases, such as normal subgroup for kernels of group homomorphisms and ideals for kernels of ring homomorphisms (in the case of non-commutative rings, the kernels are the two-sided ideals).

Relational structures

In model theory, the notion of an algebraic structure is generalized to structures involving both operations and relations. Let ''L'' be a signature consisting of function and relation symbols, and ''A'', ''B'' be two ''L''-structures. Then a homomorphism from ''A'' to ''B'' is a mapping ''h'' from the domain of ''A'' to the domain of ''B'' such that
* ''h''(''F''^''A''(''a''₁,…,''a''_''n'')) = ''F''^''B''(''h''(''a''₁),…,''h''(''a''_''n'')) for each ''n''-ary function symbol ''F'' in ''L'',
* ''R''^''A''(''a''₁,…,''a''_''n'') implies ''R''^''B''(''h''(''a''₁),…,''h''(''a''_''n'')) for each ''n''-ary relation symbol ''R'' in ''L''.
In the special case with just one binary relation, we obtain the notion of a graph homomorphism.

Formal language theory

Homomorphisms are also used in the study of formal languages and are often briefly referred to as ''morphisms''. Given alphabets $\Sigma_1$ and $\Sigma_2$, a function $h \colon \Sigma_1^* \to \Sigma_2^*$ such that $h(uv) = h(u) h(v)$ for all $u,v \in \Sigma_1$ is called a ''homomorphism'' on $\Sigma_1^*$.The ∗ denotes the Kleene star operation, while Σ^∗ denotes the set of words formed from the alphabet Σ, including the empty word. Juxtaposition of terms denotes concatenation. For example, ''h''(''u'') ''h''(''v'') denotes the concatenation of ''h''(''u'') with ''h''(''v''). If $h$ is a homomorphism on $\Sigma_1^*$ and $\varepsilon$ denotes the empty string, then $h$ is called an $\varepsilon$''-free homomorphism'' when $h(x) \neq \varepsilon$ for all $x \neq \varepsilon$ in $\Sigma_1^*$.

A homomorphism $h \colon \Sigma_1^* \to \Sigma_2^*$ on $\Sigma_1^*$ that satisfies $, h(a), = k$ for all $a \in \Sigma_1$ is called a $k$''-uniform'' homomorphism. p. 287 If $, h(a), = 1$ for all $a \in \Sigma_1$ (that is, $h$ is 1-uniform), then $h$ is also called a ''coding'' or a ''projection''.

The set $\Sigma^*$ of words formed from the alphabet $\Sigma$ may be thought of as the free monoid generated by $\Sigma$. Here the monoid operation is concatenation and the identity element is the empty word. From this perspective, a language homomorphism is precisely a monoid homomorphism.We are assured that a language homomorphism ''h'' maps the empty word ''ε'' to the empty word. Since ''h''(''ε'') = ''h''(''εε'') = ''h''(''ε'')''h''(''ε''), the number ''w'' of characters in ''h''(''ε'') equals the number 2''w'' of characters in ''h''(''ε'')''h''(''ε''). Hence ''w'' = 0 and ''h''(''ε'') has null length.

See also

* Diffeomorphism
* Homomorphic encryption
* Homomorphic secret sharing – a simplistic decentralized voting protocol
* Morphism
* Quasimorphism

Notes

Citations

References

*Krieger, Dalia (2006). "On critical exponents in fixed points of non-erasing morphisms". ''Developments in Language Theory: Proceedings 10th International Conference, DLT 2006, Santa Barbara, CA, USA, June 26–29, 2006''. Oscar H. Ibarra, Zhe Dang. Springer-Verlag. pp. 280–291. ISBN  3-540-35428-X.
*
*
*

{{Authority control

Morphisms