standard error of the mean on:
[Wikipedia]
[Google]
[Amazon]
 The standard error (SE) of a
The standard error (SE) of a
'' finite population correction'' (a.k.a.: FPC):
:
which, for large ''N'':
:
to account for the added precision gained by sampling close to a larger percentage of the population. The effect of the FPC is that the error becomes zero when the sample size ''n'' is equal to the population size ''N''.
This happens in
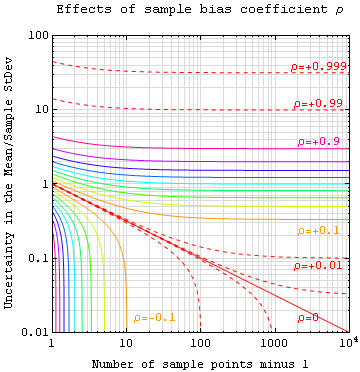 If values of the measured quantity ''A'' are not statistically independent but have been obtained from known locations in parameter space x, an unbiased estimate of the true standard error of the mean (actually a correction on the standard deviation part) may be obtained by multiplying the calculated standard error of the sample by the factor ''f'':
:
where the sample bias coefficient ρ is the widely used Prais–Winsten estimate of the
If values of the measured quantity ''A'' are not statistically independent but have been obtained from known locations in parameter space x, an unbiased estimate of the true standard error of the mean (actually a correction on the standard deviation part) may be obtained by multiplying the calculated standard error of the sample by the factor ''f'':
:
where the sample bias coefficient ρ is the widely used Prais–Winsten estimate of the
statistic
A statistic (singular) or sample statistic is any quantity computed from values in a sample which is considered for a statistical purpose. Statistical purposes include estimating a population parameter, describing a sample, or evaluating a hy ...
(usually an estimate of a parameter
A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when ...
) is the standard deviation of its sampling distribution or an estimate of that standard deviation. If the statistic is the sample mean, it is called the standard error of the mean (SEM).
The sampling distribution of a mean is generated by repeated sampling from the same population and recording of the sample means obtained. This forms a distribution of different means, and this distribution has its own mean
There are several kinds of mean in mathematics, especially in statistics. Each mean serves to summarize a given group of data, often to better understand the overall value ( magnitude and sign) of a given data set.
For a data set, the '' ari ...
and variance
In probability theory and statistics, variance is the expectation of the squared deviation of a random variable from its population mean or sample mean. Variance is a measure of dispersion, meaning it is a measure of how far a set of number ...
. Mathematically, the variance of the sampling mean distribution obtained is equal to the variance of the population divided by the sample size. This is because as the sample size increases, sample means cluster more closely around the population mean.
Therefore, the relationship between the standard error of the mean and the standard deviation is such that, for a given sample size, the standard error of the mean equals the standard deviation divided by the square root
In mathematics, a square root of a number is a number such that ; in other words, a number whose ''square'' (the result of multiplying the number by itself, or ⋅ ) is . For example, 4 and −4 are square roots of 16, because .
...
of the sample size. In other words, the standard error of the mean is a measure of the dispersion of sample means around the population mean.
In regression analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one ...
, the term "standard error" refers either to the square root of the reduced chi-squared statistic or the standard error for a particular regression coefficient (as used in, say, confidence interval
In frequentist statistics, a confidence interval (CI) is a range of estimates for an unknown parameter. A confidence interval is computed at a designated ''confidence level''; the 95% confidence level is most common, but other levels, such as ...
s).
Standard error of the sample mean
Exact value
If a statistically independent sample of observations is taken from astatistical population
In statistics, a population is a set of similar items or events which is of interest for some question or experiment. A statistical population can be a group of existing objects (e.g. the set of all stars within the Milky Way galaxy) or a hypot ...
with a standard deviation of , then the mean value calculated from the sample will have an associated ''standard error on the mean'' given by:
:.
Practically this tells us that when trying to estimate the value of a population mean, due to the factor , reducing the error on the estimate by a factor of two requires acquiring four times as many observations in the sample; reducing it by a factor of ten requires a hundred times as many observations.
Estimate
The standard deviation of the population being sampled is seldom known. Therefore, the standard error of the mean is usually estimated by replacing with thesample standard deviation
In statistics, the standard deviation is a measure of the amount of variation or dispersion of a set of values. A low standard deviation indicates that the values tend to be close to the mean (also called the expected value) of the set, while ...
instead:
:.
As this is only an estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule (the estimator), the quantity of interest (the estimand) and its result (the estimate) are distinguished. For example, the ...
for the true "standard error", it is common to see other notations here such as:
: or alternately .
A common source of confusion occurs when failing to distinguish clearly between the standard deviation of the ''population'' (), the standard deviation of the ''sample'' (), the standard deviation of the ''mean'' itself (, which is the standard error), and the ''estimator'' of the standard deviation of the mean (, which is the most often calculated quantity, and is also often colloquially called the ''standard error'').
Accuracy of the estimator
When the sample size is small, using the standard deviation of the sample instead of the true standard deviation of the population will tend to systematically underestimate the population standard deviation, and therefore also the standard error. With n = 2, the underestimate is about 25%, but for n = 6, the underestimate is only 5%. Gurland and Tripathi (1971) provide a correction and equation for this effect. Sokal and Rohlf (1981) give an equation of the correction factor for small samples of ''n'' < 20. See unbiased estimation of standard deviation for further discussion.Derivation
The standard error on the mean may be derived from thevariance
In probability theory and statistics, variance is the expectation of the squared deviation of a random variable from its population mean or sample mean. Variance is a measure of dispersion, meaning it is a measure of how far a set of number ...
of a sum of independent random variables, given the definition
A definition is a statement of the meaning of a term (a word, phrase, or other set of symbols). Definitions can be classified into two large categories: intensional definitions (which try to give the sense of a term), and extensional definitio ...
of variance and some simple properties thereof. If are independent samples from a population with mean and standard deviation , then we can define the total
:
which due to the Bienaymé formula, will have variance
:
The mean of these measurements is simply given by
:.
The variance of the mean is then
:
The standard error is, by definition, the standard deviation of which is simply the square root of the variance:
:.
For correlated random variables the sample variance needs to be computed according to the Markov chain central limit theorem.
Independent and identically distributed random variables with random sample size
There are cases when a sample is taken without knowing, in advance, how many observations will be acceptable according to some criterion. In such cases, the sample size is a random variable whose variation adds to the variation of such that, : If has a ''Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known ...
'', then with estimator . Hence the estimator of becomes , leading the following formula for standard error:
:
(since the standard deviation is the square root of the variance)
Student approximation when ''σ'' value is unknown
In many practical applications, the true value of ''σ'' is unknown. As a result, we need to use a distribution that takes into account that spread of possible ''σs. When the true underlying distribution is known to be Gaussian, although with unknown σ, then the resulting estimated distribution follows the Student t-distribution. The standard error is the standard deviation of the Student t-distribution. T-distributions are slightly different from Gaussian, and vary depending on the size of the sample. Small samples are somewhat more likely to underestimate the population standard deviation and have a mean that differs from the true population mean, and the Student t-distribution accounts for the probability of these events with somewhat heavier tails compared to a Gaussian. To estimate the standard error of a Student t-distribution it is sufficient to use the sample standard deviation "s" instead of ''σ'', and we could use this value to calculate confidence intervals. ''Note:'' The Student's probability distribution is approximated well by the Gaussian distribution when the sample size is over 100. For such samples one can use the latter distribution, which is much simpler.Assumptions and usage
An example of how is used is to make confidence intervals of the unknown population mean. If the sampling distribution isnormally distributed
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
:
f(x) = \frac e^
The parameter \mu is ...
, the sample mean, the standard error, and the quantiles of the normal distribution can be used to calculate confidence intervals for the true population mean. The following expressions can be used to calculate the upper and lower 95% confidence limits, where is equal to the sample mean, is equal to the standard error for the sample mean, and 1.96 is the approximate value of the 97.5 percentile
In statistics, a ''k''-th percentile (percentile score or centile) is a score ''below which'' a given percentage ''k'' of scores in its frequency distribution falls (exclusive definition) or a score ''at or below which'' a given percentage falls ...
point of the normal distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
:
f(x) = \frac e^
The parameter \mu i ...
:
:Upper 95% limit and
:Lower 95% limit
In particular, the standard error of a sample statistic
A statistic (singular) or sample statistic is any quantity computed from values in a sample which is considered for a statistical purpose. Statistical purposes include estimating a population parameter, describing a sample, or evaluating a hyp ...
(such as sample mean
The sample mean (or "empirical mean") and the sample covariance are statistics computed from a sample of data on one or more random variables.
The sample mean is the average value (or mean value) of a sample of numbers taken from a larger po ...
) is the actual or estimated standard deviation of the sample mean in the process by which it was generated. In other words, it is the actual or estimated standard deviation of the sampling distribution of the sample statistic. The notation for standard error can be any one of SE, SEM (for standard error of ''measurement'' or ''mean''), or SE.
Standard errors provide simple measures of uncertainty in a value and are often used because:
*in many cases, if the standard error of several individual quantities is known then the standard error of some function
Function or functionality may refer to:
Computing
* Function key, a type of key on computer keyboards
* Function model, a structured representation of processes in a system
* Function object or functor or functionoid, a concept of object-orie ...
of the quantities can be easily calculated;
*when the probability distribution
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomeno ...
of the value is known, it can be used to calculate an exact confidence interval
In frequentist statistics, a confidence interval (CI) is a range of estimates for an unknown parameter. A confidence interval is computed at a designated ''confidence level''; the 95% confidence level is most common, but other levels, such as ...
;
*when the probability distribution is unknown, Chebyshev
Pafnuty Lvovich Chebyshev ( rus, Пафну́тий Льво́вич Чебышёв, p=pɐfˈnutʲɪj ˈlʲvovʲɪtɕ tɕɪbɨˈʂof) ( – ) was a Russian mathematician and considered to be the founding father of Russian mathematics.
Chebysh ...
's or the Vysochanskiï–Petunin inequalities can be used to calculate a conservative confidence interval; and
* as the sample size
Sample size determination is the act of choosing the number of observations or replicates to include in a statistical sample. The sample size is an important feature of any empirical study in which the goal is to make inferences about a populatio ...
tends to infinity the central limit theorem
In probability theory, the central limit theorem (CLT) establishes that, in many situations, when independent random variables are summed up, their properly normalized sum tends toward a normal distribution even if the original variables thems ...
guarantees that the sampling distribution of the mean is asymptotically normal.
Standard error of mean versus standard deviation
In scientific and technical literature, experimental data are often summarized either using the mean and standard deviation of the sample data or the mean with the standard error. This often leads to confusion about their interchangeability. However, the mean and standard deviation aredescriptive statistics
A descriptive statistic (in the count noun sense) is a summary statistic that quantitatively describes or summarizes features from a collection of information, while descriptive statistics (in the mass noun sense) is the process of using and a ...
, whereas the standard error of the mean is descriptive of the random sampling process. The standard deviation of the sample data is a description of the variation in measurements, while the standard error of the mean is a probabilistic statement about how the sample size will provide a better bound on estimates of the population mean, in light of the central limit theorem.
Put simply, the standard error of the sample mean is an estimate of how far the sample mean is likely to be from the population mean, whereas the standard deviation of the sample is the degree to which individuals within the sample differ from the sample mean. If the population standard deviation is finite, the standard error of the mean of the sample will tend to zero with increasing sample size, because the estimate of the population mean will improve, while the standard deviation of the sample will tend to approximate the population standard deviation as the sample size increases.
Extensions
Finite population correction (FPC)
The formula given above for the standard error assumes that the population is infinite. Nonetheless, it is often used for finite populations when people are interested in measuring the process that created the existing finite population (this is called an analytic study). Though the above formula is not exactly correct when the population is finite, the difference between the finite- and infinite-population versions will be small whensampling fraction
In sampling theory, the sampling fraction is the ratio of sample size to population size or, in the context of stratified sampling, the ratio of the sample size to the size of the stratum.
The formula for the sampling fraction is
:f=\frac,
where ...
is small (e.g. a small proportion of a finite population is studied). In this case people often do not correct for the finite population, essentially treating it as an "approximately infinite" population.
If one is interested in measuring an existing finite population that will not change over time, then it is necessary to adjust for the population size (called an enumerative study). When the sampling fraction
In sampling theory, the sampling fraction is the ratio of sample size to population size or, in the context of stratified sampling, the ratio of the sample size to the size of the stratum.
The formula for the sampling fraction is
:f=\frac,
where ...
(often termed ''f'') is large (approximately at 5% or more) in an enumerative study, the estimate of the standard error must be corrected by multiplying by a survey methodology
Survey methodology is "the study of survey methods".
As a field of applied statistics concentrating on human-research surveys, survey methodology studies the sampling of individual units from a population and associated techniques of survey ...
when sampling without replacement. If sampling with replacement, then FPC does not come into play.
Correction for correlation in the sample
 If values of the measured quantity ''A'' are not statistically independent but have been obtained from known locations in parameter space x, an unbiased estimate of the true standard error of the mean (actually a correction on the standard deviation part) may be obtained by multiplying the calculated standard error of the sample by the factor ''f'':
:
where the sample bias coefficient ρ is the widely used Prais–Winsten estimate of the
If values of the measured quantity ''A'' are not statistically independent but have been obtained from known locations in parameter space x, an unbiased estimate of the true standard error of the mean (actually a correction on the standard deviation part) may be obtained by multiplying the calculated standard error of the sample by the factor ''f'':
:
where the sample bias coefficient ρ is the widely used Prais–Winsten estimate of the autocorrelation
Autocorrelation, sometimes known as serial correlation in the discrete time case, is the correlation of a signal with a delayed copy of itself as a function of delay. Informally, it is the similarity between observations of a random variable ...
-coefficient (a quantity between −1 and +1) for all sample point pairs. This approximate formula is for moderate to large sample sizes; the reference gives the exact formulas for any sample size, and can be applied to heavily autocorrelated time series like Wall Street stock quotes. Moreover, this formula works for positive and negative ρ alike. See also unbiased estimation of standard deviation for more discussion.
See also
* Illustration of the central limit theorem *Margin of error
The margin of error is a statistic expressing the amount of random sampling error in the results of a survey. The larger the margin of error, the less confidence one should have that a poll result would reflect the result of a census of the en ...
* Probable error In statistics, probable error defines the half-range of an interval about a central point for the distribution, such that half of the values from the distribution will lie within the interval and half outside.Dodge, Y. (2006) ''The Oxford Dictiona ...
* Standard error of the weighted mean
* Sample mean and sample covariance
The sample mean (or "empirical mean") and the sample covariance are statistics computed from a sample of data on one or more random variables.
The sample mean is the average value (or mean value) of a sample of numbers taken from a larger pop ...
* Standard error of the median
* Variance
In probability theory and statistics, variance is the expectation of the squared deviation of a random variable from its population mean or sample mean. Variance is a measure of dispersion, meaning it is a measure of how far a set of number ...
References
{{statistics, collection, state=collapsed Statistical deviation and dispersion