Stable Limit Cycle on:
[Wikipedia]
[Google]
[Amazon]
 In
In
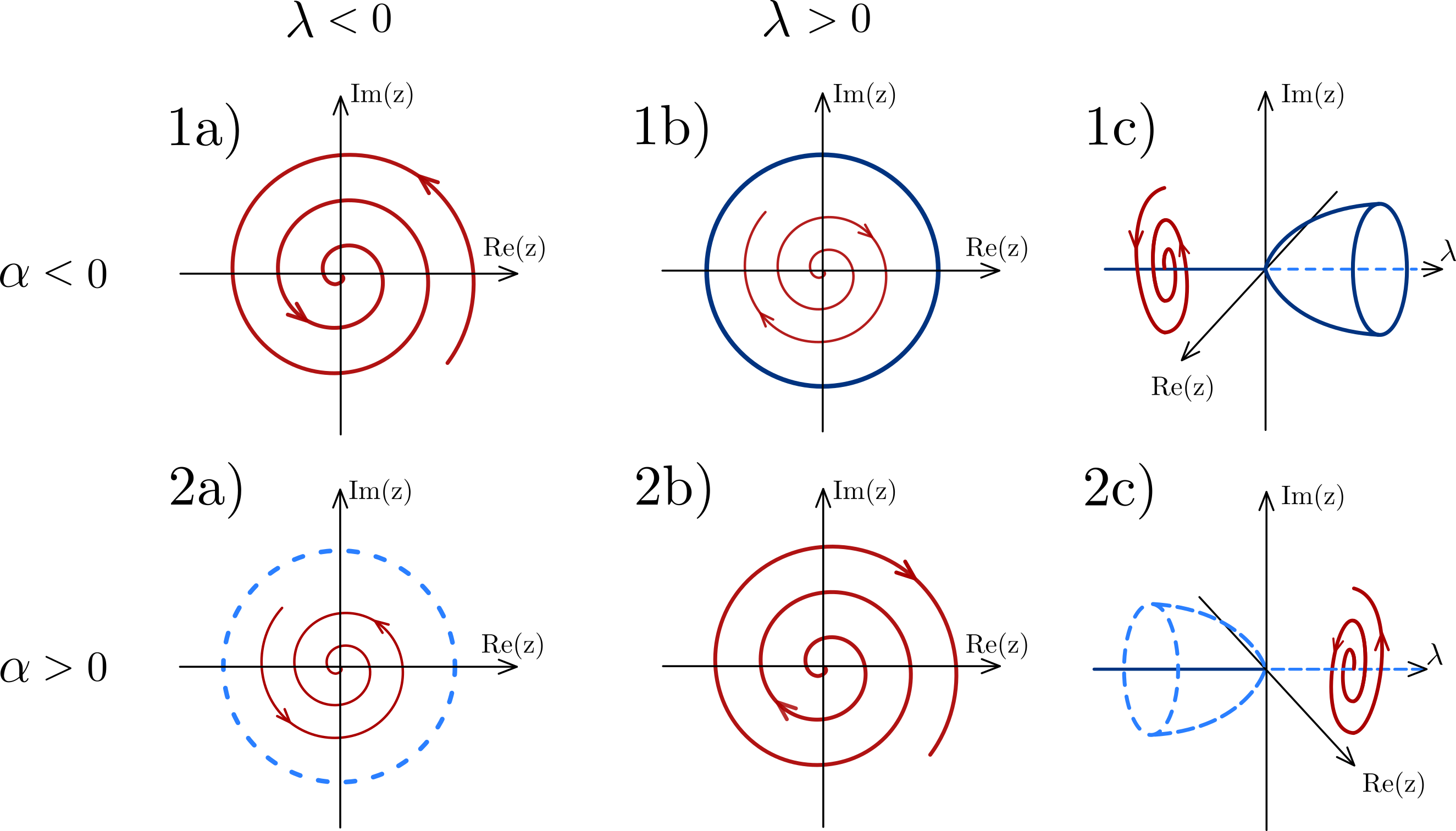 Limit cycles are important in many scientific applications where systems with self-sustained oscillations are modelled. Some examples include:
* Aerodynamic limit-cycle oscillations
* The
Limit cycles are important in many scientific applications where systems with self-sustained oscillations are modelled. Some examples include:
* Aerodynamic limit-cycle oscillations
* The
mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, in the study of dynamical systems
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a p ...
with two-dimensional phase space
In dynamical system theory, a phase space is a space in which all possible states of a system are represented, with each possible state corresponding to one unique point in the phase space. For mechanical systems, the phase space usually ...
, a limit cycle is a closed trajectory
A trajectory or flight path is the path that an object with mass in motion follows through space as a function of time. In classical mechanics, a trajectory is defined by Hamiltonian mechanics via canonical coordinates; hence, a complete traj ...
in phase space having the property that at least one other trajectory spirals into it either as time approaches infinity or as time approaches negative infinity. Such behavior is exhibited in some nonlinear systems. Limit cycles have been used to model the behavior of a great many real-world oscillatory systems. The study of limit cycles was initiated by Henri Poincaré
Jules Henri Poincaré ( S: stress final syllable ; 29 April 1854 – 17 July 1912) was a French mathematician, theoretical physicist, engineer, and philosopher of science. He is often described as a polymath, and in mathematics as "The ...
(1854–1912).
Definition
We consider a two-dimensional dynamical system of the form where is a smooth function. A ''trajectory'' of this system is some smooth function with values in which satisfies this differential equation. Such a trajectory is called ''closed'' (or ''periodic'') if it is not constant but returns to its starting point, i.e. if there exists some such that for all . Anorbit
In celestial mechanics, an orbit is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an object or position in space such as a p ...
is the image
An image is a visual representation of something. It can be two-dimensional, three-dimensional, or somehow otherwise feed into the visual system to convey information. An image can be an artifact, such as a photograph or other two-dimensiona ...
of a trajectory, a subset of . A ''closed orbit'', or ''cycle'', is the image of a closed trajectory. A ''limit cycle'' is a cycle which is the limit set of some other trajectory.
Properties
By the Jordan curve theorem, every closed trajectory divides the plane into two regions, the interior and the exterior of the curve. Given a limit cycle and a trajectory in its interior that approaches the limit cycle for time approaching , then there is a neighborhood around the limit cycle such that ''all'' trajectories in the interior that start in the neighborhood approach the limit cycle for time approaching . The corresponding statement holds for a trajectory in the interior that approaches the limit cycle for time approaching , and also for trajectories in the exterior approaching the limit cycle.Stable, unstable and semi-stable limit cycles
In the case where all the neighboring trajectories approach the limit cycle as time approaches infinity, it is called a ''stable
A stable is a building in which livestock, especially horses, are kept. It most commonly means a building that is divided into separate stalls for individual animals and livestock. There are many different types of stables in use today; the ...
'' or ''attractive'' limit cycle (ω-limit cycle). If instead, all neighboring trajectories approach it as time approaches negative infinity, then it is an ''unstable'' limit cycle (α-limit cycle). If there is a neighboring trajectory which spirals into the limit cycle as time approaches infinity, and another one which spirals into it as time approaches negative infinity, then it is a ''semi-stable'' limit cycle. There are also limit cycles that are neither stable, unstable nor semi-stable: for instance, a neighboring trajectory may approach the limit cycle from the outside, but the inside of the limit cycle is approached by a family of other cycles (which wouldn't be limit cycles).
Stable limit cycles are examples of attractors. They imply self-sustained oscillations
Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value (often a point of equilibrium) or between two or more different states. Familiar examples of oscillation include a swinging pendulum ...
: the closed trajectory describes the perfect periodic behavior of the system, and any small perturbation from this closed trajectory causes the system to return to it, making the system stick to the limit cycle.
Finding limit cycles
Every closed trajectory contains within its interior a stationary point of the system, i.e. a point where . TheBendixson–Dulac theorem In mathematics, the Bendixson–Dulac theorem on dynamical systems states that if there exists a C^1 function \varphi(x, y) (called the Dulac function) such that the expression
:\frac + \frac
has the same sign (\neq 0) almost everywhere in a ...
and the Poincaré–Bendixson theorem predict the absence or existence, respectively, of limit cycles of two-dimensional nonlinear dynamical systems.
Open problems
Finding limit cycles, in general, is a very difficult problem. The number of limit cycles of a polynomial differential equation in the plane is the main object of the second part ofHilbert's sixteenth problem
Hilbert's 16th problem was posed by David Hilbert at the Paris conference of the International Congress of Mathematicians in 1900, as part of his list of 23 problems in mathematics.
The original problem was posed as the ''Problem of the topolo ...
. It is unknown, for instance, whether there is any system in the plane where both components of are quadratic polynomials of the two variables, such that the system has more than 4 limit cycles.
Applications
 Limit cycles are important in many scientific applications where systems with self-sustained oscillations are modelled. Some examples include:
* Aerodynamic limit-cycle oscillations
* The
Limit cycles are important in many scientific applications where systems with self-sustained oscillations are modelled. Some examples include:
* Aerodynamic limit-cycle oscillations
* The Hodgkin–Huxley model
The Hodgkin–Huxley model, or conductance-based model, is a mathematical model that describes how action potentials in neurons are initiated and propagated. It is a set of nonlinear differential equations that approximates the electrical charact ...
for action potential
An action potential occurs when the membrane potential of a specific cell location rapidly rises and falls. This depolarization then causes adjacent locations to similarly depolarize. Action potentials occur in several types of animal cells, ...
s in neuron
A neuron, neurone, or nerve cell is an electrically excitable cell that communicates with other cells via specialized connections called synapses. The neuron is the main component of nervous tissue in all animals except sponges and placozoa. N ...
s.
* The Sel'kov model of glycolysis
Glycolysis is the metabolic pathway that converts glucose () into pyruvate (). The free energy released in this process is used to form the high-energy molecules adenosine triphosphate (ATP) and reduced nicotinamide adenine dinucleotide (NADH ...
.
* The daily oscillations in gene expression, hormone levels and body temperature of animals, which are part of the circadian rhythm
A circadian rhythm (), or circadian cycle, is a natural, internal process that regulates the sleep–wake cycle and repeats roughly every 24 hours. It can refer to any process that originates within an organism (i.e., Endogeny (biology), endogeno ...
, although this is contradicted by more recent evidence.
* The migration of cancer cells in confining micro-environments follows limit cycle oscillations.
* Some non-linear electrical circuits exhibit limit cycle oscillations, which inspired the original Van der Pol model.
*The control of respiration and hematopoiesis, as appearing in the Mackey-Glass equations.
See also
* Attractor *Hyperbolic set In dynamical systems theory, a subset Λ of a smooth manifold ''M'' is said to have a hyperbolic structure with respect to a smooth map ''f'' if its tangent bundle may be split into two invariant subbundles, one of which is contracting and th ...
* Periodic point
* Self-oscillation
* Stable manifold
References
Further reading
* * * Philip Hartman, "Ordinary Differential Equation", Society for Industrial and Applied Mathematics, 2002. * Witold Hurewicz, "Lectures on Ordinary Differential Equations", Dover, 2002. * Solomon Lefschetz, "Differential Equations: Geometric Theory", Dover, 2005. * Lawrence Perko, "Differential Equations and Dynamical Systems", Springer-Verlag, 2006. * Arthur Mattuck, Limit Cycles: Existence and Non-existence Criteria, MIT Open Courseware http://videolectures.net/mit1803s06_mattuck_lec32/#External links
* {{cite web , url=https://planetmath.org/limitcycle , website=planetmath.org , title=limit cycle , access-date=2019-07-06 Limit sets Nonlinear systems Dynamical systems