Squared Triangular Number on:
[Wikipedia]
[Google]
[Amazon]
 In
In
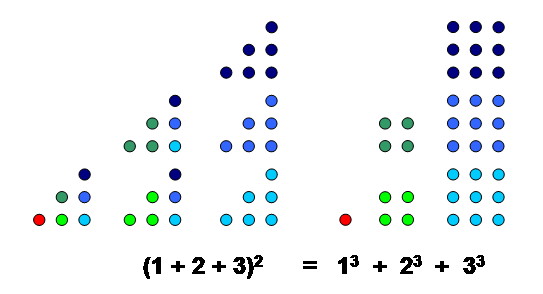 In the more recent mathematical literature, provides a proof using
In the more recent mathematical literature, provides a proof using
A visual proof of Nicomachus's theorem
{{Classes of natural numbers Number theory Integer sequences Algebraic identities Articles containing proofs Proof without words
number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. Number theorists study prime numbers as well as the properties of mathematical objects constructed from integers (for example ...
, the sum of the first cube
A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It i ...
s is the square
In geometry, a square is a regular polygon, regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal si ...
of the th triangular number
A triangular number or triangle number counts objects arranged in an equilateral triangle. Triangular numbers are a type of figurate number, other examples being square numbers and cube numbers. The th triangular number is the number of dots in ...
. That is,
:
The same equation may be written more compactly using the mathematical notation for summation
In mathematics, summation is the addition of a sequence of numbers, called ''addends'' or ''summands''; the result is their ''sum'' or ''total''. Beside numbers, other types of values can be summed as well: functions, vectors, matrices, pol ...
:
:
This identity is sometimes called Nicomachus's theorem, after Nicomachus of Gerasa
Nicomachus of Gerasa (; ) was an Ancient Greek Neopythagorean philosopher from Gerasa, in the Roman province of Syria (now Jerash, Jordan). Like many Pythagoreans, Nicomachus wrote about the mystical properties of numbers, best known for his ...
( – ).
History
Nicomachus, at the end of Chapter 20 of his ''Introduction to Arithmetic'', pointed out that if one writes a list of the odd numbers, the first is the cube of 1, the sum of the next two is the cube of 2, the sum of the next three is the cube of 3, and so on. He does not go further than this, but from this it follows that the sum of the first cubes equals the sum of the first odd numbers, that is, the odd numbers from 1 to . The average of these numbers is obviously , and there are of them, so their sum is . Many early mathematicians have studied and provided proofs of Nicomachus's theorem. claims that "every student of number theory surely must have marveled at this miraculous fact". finds references to the identity not only in the works ofNicomachus
Nicomachus of Gerasa (; ) was an Ancient Greek Neopythagorean philosopher from Gerasa, in the Roman province of Syria (now Jerash, Jordan). Like many Pythagoreans, Nicomachus wrote about the mystical properties of numbers, best known for his ...
in what is now Jordan
Jordan, officially the Hashemite Kingdom of Jordan, is a country in the Southern Levant region of West Asia. Jordan is bordered by Syria to the north, Iraq to the east, Saudi Arabia to the south, and Israel and the occupied Palestinian ter ...
in the 1st century CE, but also in those of Aryabhata
Aryabhata ( ISO: ) or Aryabhata I (476–550 CE) was the first of the major mathematician-astronomers from the classical age of Indian mathematics and Indian astronomy. His works include the '' Āryabhaṭīya'' (which mentions that in 3600 ' ...
in India
India, officially the Republic of India, is a country in South Asia. It is the List of countries and dependencies by area, seventh-largest country by area; the List of countries by population (United Nations), most populous country since ...
in the 5th century, and in those of Al-Karaji
(; c. 953 – c. 1029) was a 10th-century Persian mathematician and engineer who flourished at Baghdad. He was born in Karaj, a city near Tehran. His three principal surviving works are mathematical: ''Al-Badi' fi'l-hisab'' (''Wonderful on ...
in Persia
Iran, officially the Islamic Republic of Iran (IRI) and also known as Persia, is a country in West Asia. It borders Iraq to the west, Turkey, Azerbaijan, and Armenia to the northwest, the Caspian Sea to the north, Turkmenistan to the nort ...
. mentions several additional early mathematical works on this formula, by Al-Qabisi (10th century Arabia), Gersonides
Levi ben Gershon (1288 – 20 April 1344), better known by his Graecized name as Gersonides, or by his Latinized name Magister Leo Hebraeus, or in Hebrew by the abbreviation of first letters as ''RaLBaG'', was a medieval French Jewish philosoph ...
(, France), and Nilakantha Somayaji
Keļallur Nīlakaṇṭha Somayāji (14 June 1444 – 1544), also referred to as Keļallur Comatiri, was a mathematician and astronomer of the Kerala school of astronomy and mathematics. One of his most influential works was the comprehens ...
(, India); he reproduces Nilakantha's visual proof.
Numeric values; geometric and probabilistic interpretation
The sequence of squared triangular numbers is These numbers can be viewed as figurate numbers, a four-dimensional hyperpyramidal generalization of thetriangular number
A triangular number or triangle number counts objects arranged in an equilateral triangle. Triangular numbers are a type of figurate number, other examples being square numbers and cube numbers. The th triangular number is the number of dots in ...
s and square pyramidal numbers.
As observes, these numbers also count the number of rectangles with horizontal and vertical sides formed in an grid. For instance, the points of a grid (or a square made up of three smaller squares on a side) can form 36 different rectangles. The number of squares in a square grid is similarly counted by the square pyramidal numbers.
The identity also admits a natural probabilistic interpretation as follows. Let be four integer numbers independently and uniformly chosen at random between 1 and . Then, the probability that is the largest of the four numbers equals the probability that is at least as large as and that is at least as large as . That is, For any particular value of , the combinations of , , and that make largest form a cube so (adding the size of this cube over all choices of }) the number of combinations of for which is largest is a sum of cubes, the left hand side of the Nichomachus identity. The sets of pairs with and of pairs with form isosceles right triangles, and the set counted by the right hand side of the equation of probabilities is the Cartesian product
In mathematics, specifically set theory, the Cartesian product of two sets and , denoted , is the set of all ordered pairs where is an element of and is an element of . In terms of set-builder notation, that is
A\times B = \.
A table c ...
of these two triangles, so its size is the square of a triangular number on the right hand side of the Nichomachus identity. The probabilities themselves are respectively the left and right sides of the Nichomachus identity, normalized to make probabilities by dividing both sides
Proofs
gives a particularly simple derivation, by expanding each cube in the sum into a set of consecutive odd numbers. He begins by giving the identity That identity is related totriangular numbers
A triangular number or triangle number counts objects arranged in an equilateral triangle. Triangular numbers are a type of figurate number, other examples being square numbers and cube numbers. The th triangular number is the number of dots in ...
in the following way:
and thus the summands forming start off just after those forming all previous values up to . Applying this property, along with another well-known identity:
produces the following derivation:
obtains another proof by summing the numbers in a square multiplication table
In mathematics, a multiplication table (sometimes, less formally, a times table) is a mathematical table used to define a multiplication binary operation, operation for an algebraic system.
The decimal multiplication table was traditionally tau ...
in two different ways. The sum of the th row is times a triangular number, from which it follows that the sum of all the rows is the square of a triangular number. Alternatively, one can decompose the table into a sequence of nested gnomons, each consisting of the products in which the larger of the two terms is some fixed value. The sum within each gmonon is a cube, so the sum of the whole table is a sum of cubes.
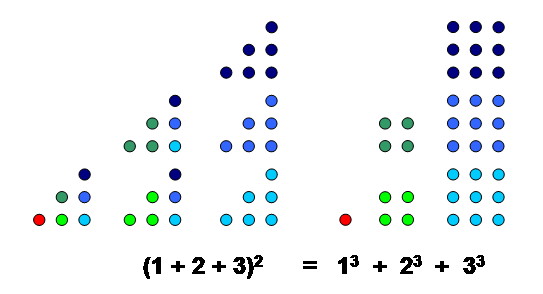 In the more recent mathematical literature, provides a proof using
In the more recent mathematical literature, provides a proof using summation by parts
In mathematics, summation by parts transforms the summation of products of sequences into other summations, often simplifying the computation or (especially) estimation of certain types of sums. It is also called Abel's lemma or Abel transformati ...
. uses the rectangle-counting interpretation of these numbers to form a geometric proof of the identity. Stein observes that it may also be proved easily (but uninformatively) by induction, and states that provides "an interesting old Arabic proof". provides a purely visual proof, provide two additional proofs, and gives seven geometric proofs.
Generalizations
A similar result to Nicomachus's theorem holds for all power sums, namely that odd power sums (sums of odd powers) are a polynomial in triangular numbers. These are called Faulhaber polynomials, of which the sum of cubes is the simplest and most elegant example. However, in no other case is one power sum a square of another. studies more general conditions under which the sum of a consecutive sequence of cubes forms a square. and study polynomial analogues of the square triangular number formula, in which series of polynomials add to the square of another polynomial.;Notes
References
*. *. *. * *. *. *. *. *. *. *. *. *. *. *.External links
*A visual proof of Nicomachus's theorem
{{Classes of natural numbers Number theory Integer sequences Algebraic identities Articles containing proofs Proof without words