spontaneously broken symmetry on:
[Wikipedia]
[Google]
[Amazon]
Spontaneous symmetry breaking is a
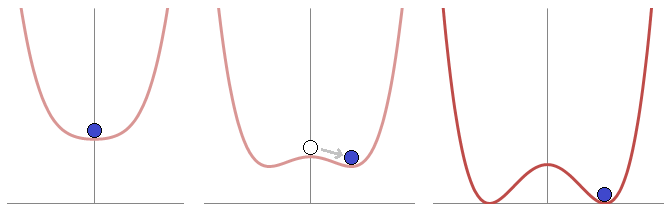 * The
* The
Spontaneous symmetry breaking
Physical Review Letters – 50th Anniversary Milestone Papers
In CERN Courier, Steven Weinberg reflects on spontaneous symmetry breaking
Englert–Brout–Higgs–Guralnik–Hagen–Kibble Mechanism on Scholarpedia
History of Englert–Brout–Higgs–Guralnik–Hagen–Kibble Mechanism on Scholarpedia
The History of the Guralnik, Hagen and Kibble development of the Theory of Spontaneous Symmetry Breaking and Gauge Particles
* [http://www.datafilehost.com/download-7d512618.html Guralnik, G S; Hagen, C R and Kibble, T W B (1967). Broken Symmetries and the Goldstone Theorem. Advances in Physics, vol. 2 Interscience Publishers, New York. pp. 567–708]
Spontaneous Symmetry Breaking in Gauge Theories: a Historical SurveyThe Royal Society Publishing: Spontaneous symmetry breaking in gauge theories
{{DEFAULTSORT:Spontaneous Symmetry Breaking Theoretical physics Quantum field theory Standard Model Quantum chromodynamics Symmetry Quantum phases
spontaneous process In thermodynamics, a spontaneous process is a process which occurs without any external input to the system. A more technical definition is the time-evolution of a system in which it releases free energy and it moves to a lower, more thermodynamic ...
of symmetry breaking
In physics, symmetry breaking is a phenomenon in which (infinitesimally) small fluctuations acting on a system crossing a critical point decide the system's fate, by determining which branch of a bifurcation is taken. To an outside observe ...
, by which a physical system in a symmetric
Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definiti ...
state spontaneously ends up in an asymmetric state. In particular, it can describe systems where the equations of motion
In physics, equations of motion are equations that describe the behavior of a physical system in terms of its motion as a function of time.''Encyclopaedia of Physics'' (second Edition), R.G. Lerner, G.L. Trigg, VHC Publishers, 1991, ISBN (Ver ...
or the Lagrangian
Lagrangian may refer to:
Mathematics
* Lagrangian function, used to solve constrained minimization problems in optimization theory; see Lagrange multiplier
** Lagrangian relaxation, the method of approximating a difficult constrained problem with ...
obey symmetries, but the lowest-energy vacuum solution
In general relativity, a vacuum solution is a Lorentzian manifold whose Einstein tensor vanishes identically. According to the Einstein field equation, this means that the stress–energy tensor also vanishes identically, so that no matter or no ...
s do not exhibit that same symmetry
Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definit ...
. When the system goes to one of those vacuum solutions, the symmetry is broken for perturbations around that vacuum even though the entire Lagrangian retains that symmetry.
Overview
By definition, spontaneous symmetry breaking requires the existence of physical laws (e.g.quantum mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, ...
) which are invariant
Invariant and invariance may refer to:
Computer science
* Invariant (computer science), an expression whose value doesn't change during program execution
** Loop invariant, a property of a program loop that is true before (and after) each iteratio ...
under a symmetry
Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definit ...
transformation (such as translation or rotation), so that any pair of outcomes differing only by that transformation have the same probability distribution. For example if measurements of an observable at any two different positions have the same probability distribution, the observable has translational symmetry.
Spontaneous symmetry breaking occurs when this relation breaks down, while the underlying physical laws remain symmetrical.
Conversely, in explicit symmetry breaking
In theoretical physics, explicit symmetry breaking is the breaking of a symmetry of a theory by terms in its defining equations of motion (most typically, to the Lagrangian or the Hamiltonian) that do not respect the symmetry. Usually this term i ...
, if two outcomes are considered, the probability distributions of a pair of outcomes can be different. For example in an electric field, the forces on a charged particle are different in different directions, so the rotational symmetry is explicitly broken by the electric field which does not have this symmetry.
Phases of matter, such as crystals, magnets, and conventional superconductors, as well as simple phase transitions can be described by spontaneous symmetry breaking. Notable exceptions include topological phases of matter like the fractional quantum Hall effect
The fractional quantum Hall effect (FQHE) is a physical phenomenon in which the Hall conductance of 2-dimensional (2D) electrons shows precisely quantized plateaus at fractional values of e^2/h. It is a property of a collective state in which elec ...
.
Typically, when spontaneous symmetry breaking occurs, the observable properties of the system change in multiple ways. For example the density, compressibility, coefficient of thermal expansion, and specific heat will be expected to change when a liquid becomes a solid.
Examples
Sombrero potential
Consider a symmetric upward dome with a trough circling the bottom. If a ball is put at the very peak of the dome, the system is symmetric with respect to a rotation around the center axis. But the ball may ''spontaneously break'' this symmetry by rolling down the dome into the trough, a point of lowest energy. Afterward, the ball has come to a rest at some fixed point on the perimeter. The dome and the ball retain their individual symmetry, but the system does not. In the simplest idealized relativistic model, the spontaneously broken symmetry is summarized through an illustrativescalar field theory
In theoretical physics, scalar field theory can refer to a relativistically invariant classical or quantum theory of scalar fields. A scalar field is invariant under any Lorentz transformation.
The only fundamental scalar quantum field that has b ...
. The relevant Lagrangian
Lagrangian may refer to:
Mathematics
* Lagrangian function, used to solve constrained minimization problems in optimization theory; see Lagrange multiplier
** Lagrangian relaxation, the method of approximating a difficult constrained problem with ...
of a scalar field , which essentially dictates how a system behaves, can be split up into kinetic and potential terms,
It is in this potential term that the symmetry breaking is triggered. An example of a potential, due to Jeffrey Goldstone
Jeffrey Goldstone (born 3 September 1933) is a British theoretical physicist and an ''emeritus'' physics faculty member at the MIT Center for Theoretical Physics.
He worked at the University of Cambridge until 1977. He is famous for the discove ...
is illustrated in the graph at the left.
This potential has an infinite number of possible minima
In mathematical analysis, the maxima and minima (the respective plurals of maximum and minimum) of a function, known collectively as extrema (the plural of extremum), are the largest and smallest value of the function, either within a given ran ...
(vacuum states) given by
for any real ''θ'' between 0 and 2''π''. The system also has an unstable vacuum state corresponding to . This state has a U(1)
In mathematics, the circle group, denoted by \mathbb T or \mathbb S^1, is the multiplicative group of all complex numbers with absolute value 1, that is, the unit circle in the complex plane or simply the unit complex numbers.
\mathbb T = \.
...
symmetry. However, once the system falls into a specific stable vacuum state (amounting to a choice of ''θ''), this symmetry will appear to be lost, or "spontaneously broken".
In fact, any other choice of ''θ'' would have exactly the same energy, and the defining equations respect the symmetry but the ground state (vacuum) of the theory breaks the symmetry, implying the existence of a massless Nambu–Goldstone boson, the mode running around the circle at the minimum of this potential, and indicating there is some memory of the original symmetry in the Lagrangian.
Other examples
* Forferromagnet
Ferromagnetism is a property of certain materials (such as iron) which results in a large observed magnetic permeability, and in many cases a large magnetic coercivity allowing the material to form a permanent magnet. Ferromagnetic materials ...
ic materials, the underlying laws are invariant under spatial rotations. Here, the order parameter is the magnetization
In classical electromagnetism, magnetization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material. Movement within this field is described by direction and is either Axial or Di ...
, which measures the magnetic dipole density. Above the Curie temperature
In physics and materials science, the Curie temperature (''T''C), or Curie point, is the temperature above which certain materials lose their permanent magnetic properties, which can (in most cases) be replaced by induced magnetism. The Cur ...
, the order parameter is zero, which is spatially invariant, and there is no symmetry breaking. Below the Curie temperature, however, the magnetization acquires a constant nonvanishing value, which points in a certain direction (in the idealized situation where we have full equilibrium; otherwise, translational symmetry gets broken as well). The residual rotational symmetries which leave the orientation of this vector invariant remain unbroken, unlike the other rotations which do not and are thus spontaneously broken.
* The laws describing a solid are invariant under the full Euclidean group, but the solid itself spontaneously breaks this group down to a space group
In mathematics, physics and chemistry, a space group is the symmetry group of an object in space, usually in three dimensions. The elements of a space group (its symmetry operations) are the rigid transformations of an object that leave it unchan ...
. The displacement and the orientation are the order parameters.
* General relativity has a Lorentz symmetry, but in FRW cosmological models, the mean 4-velocity field defined by averaging over the velocities of the galaxies (the galaxies act like gas particles at cosmological scales) acts as an order parameter breaking this symmetry. Similar comments can be made about the cosmic microwave background.
* For the electroweak
In particle physics, the electroweak interaction or electroweak force is the unified description of two of the four known fundamental interactions of nature: electromagnetism and the weak interaction. Although these two forces appear very differe ...
model, as explained earlier, a component of the Higgs field provides the order parameter breaking the electroweak gauge symmetry to the electromagnetic gauge symmetry. Like the ferromagnetic example, there is a phase transition at the electroweak temperature. The same comment about us not tending to notice broken symmetries suggests why it took so long for us to discover electroweak unification.
* In superconductors, there is a condensed-matter collective field ψ, which acts as the order parameter breaking the electromagnetic gauge symmetry.
* Take a thin cylindrical plastic rod and push both ends together. Before buckling, the system is symmetric under rotation, and so visibly cylindrically symmetric. But after buckling, it looks different, and asymmetric. Nevertheless, features of the cylindrical symmetry are still there: ignoring friction, it would take no force to freely spin the rod around, displacing the ground state in time, and amounting to an oscillation of vanishing frequency, unlike the radial oscillations in the direction of the buckle. This spinning mode is effectively the requisite Nambu–Goldstone boson.
* Consider a uniform layer of fluid
In physics, a fluid is a liquid, gas, or other material that continuously deforms (''flows'') under an applied shear stress, or external force. They have zero shear modulus, or, in simpler terms, are substances which cannot resist any shear ...
over an infinite horizontal plane. This system has all the symmetries of the Euclidean plane. But now heat the bottom surface uniformly so that it becomes much hotter than the upper surface. When the temperature gradient becomes large enough, convection cell
In the field of fluid dynamics, a convection cell is the phenomenon that occurs when density differences exist within a body of liquid or gas. These density differences result in rising and/or falling currents, which are the key characteristics ...
s will form, breaking the Euclidean symmetry.
* Consider a bead on a circular hoop that is rotated about a vertical diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle. It can also be defined as the longest chord of the circle. Both definitions are also valid for ...
. As the rotational velocity
In physics, angular velocity or rotational velocity ( or ), also known as angular frequency vector,(UP1) is a pseudovector representation of how fast the angular position or orientation of an object changes with time (i.e. how quickly an obje ...
is increased gradually from rest, the bead will initially stay at its initial equilibrium point
In mathematics, specifically in differential equations, an equilibrium point is a constant solution to a differential equation.
Formal definition
The point \tilde\in \mathbb^n is an equilibrium point for the differential equation
:\frac = \ ...
at the bottom of the hoop (intuitively stable, lowest gravitational potential
In classical mechanics, the gravitational potential at a location is equal to the work (energy transferred) per unit mass that would be needed to move an object to that location from a fixed reference location. It is analogous to the electric ...
). At a certain critical rotational velocity, this point will become unstable and the bead will jump to one of two other newly created equilibria, equidistant
A point is said to be equidistant from a set of objects if the distances between that point and each object in the set are equal.
In two-dimensional Euclidean geometry, the locus of points equidistant from two given (different) points is the ...
from the center. Initially, the system is symmetric with respect to the diameter, yet after passing the critical velocity, the bead ends up in one of the two new equilibrium points, thus breaking the symmetry.
 * The
* The two-balloon experiment
The two-balloon experiment is an experiment involving interconnected balloons. It is used in physics classes as a demonstration of elasticity.
Two identical balloons are inflated to different diameters and connected by means of a tube. The flow ...
is an example of spontaneous symmetry breaking when both balloons are initially inflated to the local maximum pressure. When some air flows from one balloon into the other, the pressure in both balloons will drop, making the system more stable in the asymmetric state.
In particle physics
Inparticle physics
Particle physics or high energy physics is the study of fundamental particles and forces that constitute matter and radiation. The fundamental particles in the universe are classified in the Standard Model as fermions (matter particles) an ...
, the force carrier In quantum field theory, a force carrier, also known as messenger particle or intermediate particle, is a type of particle that gives rise to forces between other particles. These particles serve as the quanta of a particular kind of physical fi ...
particles are normally specified by field equations with gauge symmetry; their equations predict that certain measurements will be the same at any point in the field. For instance, field equations might predict that the mass of two quarks is constant. Solving the equations to find the mass of each quark might give two solutions. In one solution, quark A is heavier than quark B. In the second solution, quark B is heavier than quark A ''by the same amount''. The symmetry of the equations is not reflected by the individual solutions, but it is reflected by the range of solutions.
An actual measurement reflects only one solution, representing a breakdown in the symmetry of the underlying theory. "Hidden" is a better term than "broken", because the symmetry is always there in these equations. This phenomenon is called ''spontaneous'' symmetry breaking (SSB) because ''nothing'' (that we know of) breaks the symmetry in the equations. By the nature of spontaneous symmetry breaking, different portions of the early Universe would break symmetry in different directions, leading to topological defect
A topological soliton occurs when two adjoining structures or spaces are in some way "out of phase" with each other in ways that make a seamless transition between them impossible. One of the simplest and most commonplace examples of a topological ...
s, such as two-dimensional domain walls
A domain wall is a type of topological soliton that occurs whenever a discrete symmetry is spontaneously broken. Domain walls are also sometimes called kinks in analogy with closely related kink solution of the sine-Gordon model or models with pol ...
, one-dimensional cosmic strings
Cosmic strings are hypothetical 1-dimensional topological defects which may have formed during a symmetry-breaking phase transition in the early universe when the topology of the vacuum manifold associated to this symmetry breaking was not simp ...
, zero-dimensional monopoles, and/or texture
Texture may refer to:
Science and technology
* Surface texture, the texture means smoothness, roughness, or bumpiness of the surface of an object
* Texture (roads), road surface characteristics with waves shorter than road roughness
* Texture ...
s, depending on the relevant homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, denoted \pi_1(X), which records information about loops in a space. Intuitively, homotop ...
and the dynamics of the theory. For example, Higgs symmetry breaking may have created primordial cosmic strings as a byproduct. Hypothetical GUT symmetry-breaking generically produces monopoles, creating difficulties for GUT unless monopoles (along with any GUT domain walls) are expelled from our observable Universe through cosmic inflation.
Chiral symmetry
Chiral symmetry breaking is an example of spontaneous symmetry breaking affecting thechiral symmetry
A chiral phenomenon is one that is not identical to its mirror image (see the article on mathematical chirality). The spin of a particle may be used to define a handedness, or helicity, for that particle, which, in the case of a massless particle, ...
of the strong interactions in particle physics. It is a property of quantum chromodynamics
In theoretical physics, quantum chromodynamics (QCD) is the theory of the strong interaction between quarks mediated by gluons. Quarks are fundamental particles that make up composite hadrons such as the proton, neutron and pion. QCD is a type ...
, the quantum field theory
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines classical field theory, special relativity, and quantum mechanics. QFT is used in particle physics to construct physical models of subatomic particles and ...
describing these interactions, and is responsible for the bulk of the mass (over 99%) of the nucleons
In physics and chemistry, a nucleon is either a proton or a neutron, considered in its role as a component of an atomic nucleus. The number of nucleons in a nucleus defines the atom's mass number (nucleon number).
Until the 1960s, nucleons we ...
, and thus of all common matter, as it converts very light bound quarks
A quark () is a type of elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. All commonly ...
into 100 times heavier constituents of baryons
In particle physics, a baryon is a type of composite subatomic particle which contains an odd number of valence quarks (at least 3). Baryons belong to the hadron family of particles; hadrons are composed of quarks. Baryons are also classified ...
. The approximate Nambu–Goldstone bosons in this spontaneous symmetry breaking process are the pions
In particle physics, a pion (or a pi meson, denoted with the Greek letter pi: ) is any of three subatomic particles: , , and . Each pion consists of a quark and an antiquark and is therefore a meson. Pions are the lightest mesons and, more gene ...
, whose mass is an order of magnitude lighter than the mass of the nucleons. It served as the prototype and significant ingredient of the Higgs mechanism underlying the electroweak symmetry breaking.
Higgs mechanism
The strong, weak, and electromagnetic forces can all be understood as arising from gauge symmetries, which is a redundancy in the description of the symmetry. TheHiggs mechanism
In the Standard Model of particle physics, the Higgs mechanism is essential to explain the generation mechanism of the property "mass" for gauge bosons. Without the Higgs mechanism, all bosons (one of the two classes of particles, the other be ...
, the spontaneous symmetry breaking of gauge symmetries, is an important component in understanding the superconductivity
Superconductivity is a set of physical properties observed in certain materials where electrical resistance vanishes and magnetic flux fields are expelled from the material. Any material exhibiting these properties is a superconductor. Unlike ...
of metals and the origin of particle masses in the standard model of particle physics.
The term "spontaneous symmetry breaking" is a misnomer here as Elitzur's theorem
In quantum field theory and statistical field theory, Elitzur's theorem states that in gauge theories, the only operators that can have non-vanishing expectation values are ones that are invariant under local gauge transformations. An important i ...
states that local gauge symmetries can never be spontaneously broken. Rather, after gauge fixing, the global symmetry (or redundancy) can be broken in a manner formally resembling spontaneous symmetry breaking.
One important consequence of the distinction between true symmetries and ''gauge symmetries'', is that the massless Nambu–Goldstone resulting from spontaneous breaking of a gauge symmetry are absorbed in the description of the gauge vector field, providing massive vector field modes, like the plasma mode in a superconductor, or the Higgs mode observed in particle physics.
In the standard model of particle physics, spontaneous symmetry breaking of the gauge symmetry associated with the electro-weak force generates masses for several particles, and separates the electromagnetic and weak forces. The W and Z bosons
In particle physics, the W and Z bosons are vector bosons that are together known as the weak bosons or more generally as the intermediate vector bosons. These elementary particles mediate the weak interaction; the respective symbols are , , and ...
are the elementary particles that mediate the weak interaction
In nuclear physics and particle physics, the weak interaction, which is also often called the weak force or weak nuclear force, is one of the four known fundamental interactions, with the others being electromagnetism, the strong interaction, ...
, while the photon
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless, so they always ...
mediates the electromagnetic interaction
In physics, electromagnetism is an interaction that occurs between particles with electric charge. It is the second-strongest of the four fundamental interactions, after the strong force, and it is the dominant force in the interactions of ...
. At energies much greater than 100 GeV, all these particles behave in a similar manner. The Weinberg–Salam theory predicts that, at lower energies, this symmetry is broken so that the photon and the massive W and Z bosons emerge. In addition, fermions develop mass consistently.
Without spontaneous symmetry breaking, the Standard Model
The Standard Model of particle physics is the theory describing three of the four known fundamental forces (electromagnetism, electromagnetic, weak interaction, weak and strong interactions - excluding gravity) in the universe and classifying a ...
of elementary particle interactions requires the existence of a number of particles. However, some particles (the W and Z bosons
In particle physics, the W and Z bosons are vector bosons that are together known as the weak bosons or more generally as the intermediate vector bosons. These elementary particles mediate the weak interaction; the respective symbols are , , and ...
) would then be predicted to be massless, when, in reality, they are observed to have mass. To overcome this, spontaneous symmetry breaking is augmented by the Higgs mechanism
In the Standard Model of particle physics, the Higgs mechanism is essential to explain the generation mechanism of the property "mass" for gauge bosons. Without the Higgs mechanism, all bosons (one of the two classes of particles, the other be ...
to give these particles mass. It also suggests the presence of a new particle, the Higgs boson, detected in 2012.
Superconductivity
Superconductivity is a set of physical properties observed in certain materials where electrical resistance vanishes and magnetic flux fields are expelled from the material. Any material exhibiting these properties is a superconductor. Unlike ...
of metals is a condensed-matter analog of the Higgs phenomena, in which a condensate of Cooper pairs of electrons spontaneously breaks the U(1) gauge symmetry associated with light and electromagnetism.
Dynamical symmetry breaking
Dynamical symmetry breaking (DSB) is a special form of spontaneous symmetry breaking in which the ground state of the system has reduced symmetry properties compared to its theoretical description (i.e.,Lagrangian
Lagrangian may refer to:
Mathematics
* Lagrangian function, used to solve constrained minimization problems in optimization theory; see Lagrange multiplier
** Lagrangian relaxation, the method of approximating a difficult constrained problem with ...
).
Dynamical breaking of a global symmetry is a spontaneous symmetry breaking, which happens not at the (classical) tree level (i.e., at the level of the bare action), but due to quantum corrections (i.e., at the level of the effective action
In quantum field theory, the quantum effective action is a modified expression for the classical action taking into account quantum corrections while ensuring that the principle of least action applies, meaning that extremizing the effective ac ...
).
Dynamical breaking of a gauge symmetry is subtler. In the conventional spontaneous gauge symmetry breaking, there exists an unstable Higgs particle
The Higgs boson, sometimes called the Higgs particle, is an elementary particle in the Standard Model of particle physics produced by the quantum excitation of the Higgs field,
one of the fields in particle physics theory. In the Stand ...
in the theory, which drives the vacuum to a symmetry-broken phase. (See, for example, electroweak interaction
In particle physics, the electroweak interaction or electroweak force is the unified description of two of the four known fundamental interactions of nature: electromagnetism and the weak interaction. Although these two forces appear very differe ...
.) In dynamical gauge symmetry breaking, however, no unstable Higgs particle operates in the theory, but the bound states of the system itself provide the unstable fields that render the phase transition. For example, Bardeen, Hill, and Lindner published a paper that attempts to replace the conventional Higgs mechanism
In the Standard Model of particle physics, the Higgs mechanism is essential to explain the generation mechanism of the property "mass" for gauge bosons. Without the Higgs mechanism, all bosons (one of the two classes of particles, the other be ...
in the standard model
The Standard Model of particle physics is the theory describing three of the four known fundamental forces (electromagnetism, electromagnetic, weak interaction, weak and strong interactions - excluding gravity) in the universe and classifying a ...
by a DSB that is driven by a bound state of top-antitop quarks. (Such models, in which a composite particle plays the role of the Higgs boson, are often referred to as "Composite Higgs models".) Dynamical breaking of gauge symmetries is often due to creation of a fermionic condensate
A fermionic condensate or Fermi–Dirac condensate is a superfluid phase formed by fermionic particles at low temperatures. It is closely related to the Bose–Einstein condensate, a superfluid phase formed by bosonic atoms under similar cond ...
— e.g., the quark condensate
A fermionic condensate or Fermi–Dirac condensate is a superfluid phase formed by fermionic particles at low temperatures. It is closely related to the Bose–Einstein condensate, a superfluid phase formed by bosonic atoms under similar cond ...
, which is connected to the dynamical breaking of chiral symmetry in quantum chromodynamics
In theoretical physics, quantum chromodynamics (QCD) is the theory of the strong interaction between quarks mediated by gluons. Quarks are fundamental particles that make up composite hadrons such as the proton, neutron and pion. QCD is a type ...
. Conventional superconductivity
Superconductivity is a set of physical properties observed in certain materials where electrical resistance vanishes and magnetic flux fields are expelled from the material. Any material exhibiting these properties is a superconductor. Unlike ...
is the paradigmatic example from the condensed matter side, where phonon-mediated attractions lead electrons to become bound in pairs and then condense, thereby breaking the electromagnetic gauge symmetry.
In condensed matter physics
Most phases of matter can be understood through the lens of spontaneous symmetry breaking. For example, crystals are periodic arrays of atoms that are not invariant under all translations (only under a small subset of translations by a lattice vector). Magnets have north and south poles that are oriented in a specific direction, breakingrotational symmetry
Rotational symmetry, also known as radial symmetry in geometry, is the property a shape has when it looks the same after some rotation by a partial turn. An object's degree of rotational symmetry is the number of distinct orientations in which i ...
. In addition to these examples, there are a whole host of other symmetry-breaking phases of matter — including nematic phases of liquid crystals, charge- and spin-density waves, superfluids, and many others.
There are several known examples of matter that cannot be described by spontaneous symmetry breaking, including: topologically ordered phases of matter, such as fractional quantum Hall liquids, and spin-liquids. These states do not break any symmetry, but are distinct phases of matter. Unlike the case of spontaneous symmetry breaking, there is not a general framework for describing such states.
Continuous symmetry
The ferromagnet is the canonical system that spontaneously breaks the continuous symmetry of the spins below theCurie temperature
In physics and materials science, the Curie temperature (''T''C), or Curie point, is the temperature above which certain materials lose their permanent magnetic properties, which can (in most cases) be replaced by induced magnetism. The Cur ...
and at , where ''h'' is the external magnetic field. Below the Curie temperature
In physics and materials science, the Curie temperature (''T''C), or Curie point, is the temperature above which certain materials lose their permanent magnetic properties, which can (in most cases) be replaced by induced magnetism. The Cur ...
, the energy of the system is invariant under inversion of the magnetization ''m''(x) such that . The symmetry is spontaneously broken as when the Hamiltonian becomes invariant under the inversion transformation, but the expectation value is not invariant.
Spontaneously-symmetry-broken phases of matter are characterized by an order parameter that describes the quantity which breaks the symmetry under consideration. For example, in a magnet, the order parameter is the local magnetization.
Spontaneous breaking of a continuous symmetry is inevitably accompanied by gapless (meaning that these modes do not cost any energy to excite) Nambu–Goldstone modes associated with slow, long-wavelength fluctuations of the order parameter. For example, vibrational modes in a crystal, known as phonons, are associated with slow density fluctuations of the crystal's atoms. The associated Goldstone mode for magnets are oscillating waves of spin known as spin-waves. For symmetry-breaking states, whose order parameter is not a conserved quantity, Nambu–Goldstone modes are typically massless and propagate at a constant velocity.
An important theorem, due to Mermin and Wagner, states that, at finite temperature, thermally activated fluctuations of Nambu–Goldstone modes destroy the long-range order, and prevent spontaneous symmetry breaking in one- and two-dimensional systems. Similarly, quantum fluctuations of the order parameter prevent most types of continuous symmetry breaking in one-dimensional systems even at zero temperature. (An important exception is ferromagnets, whose order parameter, magnetization, is an exactly conserved quantity and does not have any quantum fluctuations.)
Other long-range interacting systems, such as cylindrical curved surfaces interacting via the Coulomb potential
The electric potential (also called the ''electric field potential'', potential drop, the electrostatic potential) is defined as the amount of work energy needed to move a unit of electric charge from a reference point to the specific point in ...
or Yukawa potential
In particle, atomic and condensed matter physics, a Yukawa potential (also called a screened Coulomb potential) is a potential named after the Japanese physicist Hideki Yukawa. The potential is of the form:
:V_\text(r)= -g^2\frac,
where is a ...
, have been shown to break translational and rotational symmetries. It was shown, in the presence of a symmetric Hamiltonian, and in the limit of infinite volume, the system spontaneously adopts a chiral configuration — i.e., breaks mirror plane
In mathematics, a reflection (also spelled reflexion) is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as a set of fixed points; this set is called the axis (in dimension 2) or plane (in dimension 3) of ref ...
symmetry
Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definit ...
.
Generalisation and technical usage
For spontaneous symmetry breaking to occur, there must be a system in which there are several equally likely outcomes. The system as a whole is thereforesymmetric
Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definiti ...
with respect to these outcomes. However, if the system is sampled (i.e. if the system is actually used or interacted with in any way), a specific outcome must occur. Though the system as a whole is symmetric, it is never encountered with this symmetry, but only in one specific asymmetric state. Hence, the symmetry is said to be spontaneously broken in that theory. Nevertheless, the fact that each outcome is equally likely is a reflection of the underlying symmetry, which is thus often dubbed "hidden symmetry", and has crucial formal consequences. (See the article on the Goldstone boson
In particle and condensed matter physics, Goldstone bosons or Nambu–Goldstone bosons (NGBs) are bosons that appear necessarily in models exhibiting spontaneous breakdown of continuous symmetries. They were discovered by Yoichiro Nambu in par ...
.)
When a theory is symmetric with respect to a symmetry group
In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient ...
, but requires that one element of the group be distinct, then spontaneous symmetry breaking has occurred. The theory must not dictate ''which'' member is distinct, only that ''one is''. From this point on, the theory can be treated as if this element actually is distinct, with the proviso that any results found in this way must be resymmetrized, by taking the average of each of the elements of the group being the distinct one.
The crucial concept in physics theories is the order parameter
In chemistry, thermodynamics, and other related fields, a phase transition (or phase change) is the physical process of transition between one state of a medium and another. Commonly the term is used to refer to changes among the basic states of ...
. If there is a field (often a background field) which acquires an expectation value (not necessarily a ''vacuum'' expectation value) which is not invariant under the symmetry in question, we say that the system is in the ordered phase
In physics, the terms order and disorder designate the presence or absence of some symmetry or correlation in a many-particle system.
In condensed matter physics, systems typically are ordered at low temperatures; upon heating, they undergo on ...
, and the symmetry is spontaneously broken. This is because other subsystems interact with the order parameter, which specifies a "frame of reference" to be measured against. In that case, the vacuum state
In quantum field theory, the quantum vacuum state (also called the quantum vacuum or vacuum state) is the quantum state with the lowest possible energy. Generally, it contains no physical particles. The word zero-point field is sometimes used as ...
does not obey the initial symmetry (which would keep it invariant, in the linearly realized Wigner mode in which it would be a singlet), and, instead changes under the (hidden) symmetry, now implemented in the (nonlinear) Nambu–Goldstone mode. Normally, in the absence of the Higgs mechanism, massless Goldstone boson
In particle and condensed matter physics, Goldstone bosons or Nambu–Goldstone bosons (NGBs) are bosons that appear necessarily in models exhibiting spontaneous breakdown of continuous symmetries. They were discovered by Yoichiro Nambu in par ...
s arise.
The symmetry group can be discrete, such as the space group
In mathematics, physics and chemistry, a space group is the symmetry group of an object in space, usually in three dimensions. The elements of a space group (its symmetry operations) are the rigid transformations of an object that leave it unchan ...
of a crystal, or continuous (e.g., a Lie group
In mathematics, a Lie group (pronounced ) is a group that is also a differentiable manifold. A manifold is a space that locally resembles Euclidean space, whereas groups define the abstract concept of a binary operation along with the additio ...
), such as the rotational symmetry of space. However, if the system contains only a single spatial dimension, then only discrete symmetries may be broken in a vacuum state
In quantum field theory, the quantum vacuum state (also called the quantum vacuum or vacuum state) is the quantum state with the lowest possible energy. Generally, it contains no physical particles. The word zero-point field is sometimes used as ...
of the full quantum theory
Quantum theory may refer to:
Science
*Quantum mechanics, a major field of physics
*Old quantum theory, predating modern quantum mechanics
* Quantum field theory, an area of quantum mechanics that includes:
** Quantum electrodynamics
** Quantum ...
, although a classical solution may break a continuous symmetry.
Nobel Prize
On October 7, 2008, theRoyal Swedish Academy of Sciences
The Royal Swedish Academy of Sciences ( sv, Kungliga Vetenskapsakademien) is one of the Swedish Royal Academies, royal academies of Sweden. Founded on 2 June 1739, it is an independent, non-governmental scientific organization that takes special ...
awarded the 2008 Nobel Prize in Physics
)
, image = Nobel Prize.png
, alt = A golden medallion with an embossed image of a bearded man facing left in profile. To the left of the man is the text "ALFR•" then "NOBEL", and on the right, the text (smaller) "NAT•" then " ...
to three scientists for their work in subatomic physics symmetry breaking. Yoichiro Nambu
was a Japanese-American physicist and professor at the University of Chicago. Known for his contributions to the field of theoretical physics, he was awarded half of the Nobel Prize in Physics in 2008 for the discovery in 1960 of the mechanism ...
, of the University of Chicago
The University of Chicago (UChicago, Chicago, U of C, or UChi) is a private research university in Chicago, Illinois. Its main campus is located in Chicago's Hyde Park neighborhood. The University of Chicago is consistently ranked among the b ...
, won half of the prize for the discovery of the mechanism of spontaneous broken symmetry in the context of the strong interactions, specifically chiral symmetry breaking
In particle physics, chiral symmetry breaking is the spontaneous symmetry breaking of a chiral symmetry – usually by a gauge theory such as quantum chromodynamics, the quantum field theory of the strong interaction. Yoichiro Nambu was awar ...
. Physicists Makoto Kobayashi and Toshihide Maskawa
was a Japanese theoretical physicist known for his work on CP-violation who was awarded one quarter of the 2008 Nobel Prize in Physics "for the discovery of the origin of the broken symmetry which predicts the existence of at least three famili ...
, of Kyoto University
, mottoeng = Freedom of academic culture
, established =
, type = National university, Public (National)
, endowment = ¥ 316 billion (2.4 1000000000 (number), billion USD)
, faculty = 3,480 (Teaching Staff)
, administrative_staff ...
, shared the other half of the prize for discovering the origin of the explicit breaking of CP symmetry in the weak interactions. This origin is ultimately reliant on the Higgs mechanism, but, so far understood as a "just so" feature of Higgs couplings, not a spontaneously broken symmetry phenomenon.
See also
*Autocatalytic reactions and order creation
A single chemical reaction is said to be autocatalytic if one of the reaction products is also a catalyst for the same or a coupled reaction.Steinfeld J.I., Francisco J.S. and Hase W.L. ''Chemical Kinetics and Dynamics'' (2nd ed., Prentice-Hall 199 ...
* Catastrophe theory
* Chiral symmetry breaking
In particle physics, chiral symmetry breaking is the spontaneous symmetry breaking of a chiral symmetry – usually by a gauge theory such as quantum chromodynamics, the quantum field theory of the strong interaction. Yoichiro Nambu was awar ...
* CP-violation
In particle physics, CP violation is a violation of CP-symmetry (or charge conjugation parity symmetry): the combination of C-symmetry (charge symmetry) and P-symmetry (parity symmetry). CP-symmetry states that the laws of physics should be the ...
* Fermi ball In cosmology, Fermi balls are hypothetical objects that may have been created in the early history of the universe by spontaneous symmetry breaking. One paper has described them as "charged SLAC-bag type structures". Fermi balls can be modeled as a ...
* Gauge gravitation theory
In quantum field theory, gauge gravitation theory is the effort to extend Yang–Mills theory, which provides a universal description of the fundamental interactions, to describe gravity.
''Gauge gravitation theory'' should not be confused with th ...
* Goldstone boson
In particle and condensed matter physics, Goldstone bosons or Nambu–Goldstone bosons (NGBs) are bosons that appear necessarily in models exhibiting spontaneous breakdown of continuous symmetries. They were discovered by Yoichiro Nambu in par ...
* Grand unified theory
A Grand Unified Theory (GUT) is a model in particle physics in which, at high energies, the three gauge interactions of the Standard Model comprising the electromagnetic, weak, and strong forces are merged into a single force. Although this ...
* Higgs mechanism
In the Standard Model of particle physics, the Higgs mechanism is essential to explain the generation mechanism of the property "mass" for gauge bosons. Without the Higgs mechanism, all bosons (one of the two classes of particles, the other be ...
* Higgs boson
* Higgs field (classical)
Spontaneous symmetry breaking, a vacuum Higgs field, and its associated fundamental particle the Higgs boson are quantum phenomena. A vacuum Higgs field is responsible for spontaneous symmetry breaking the gauge symmetries of fundamental interact ...
* Irreversibility
In science, a process that is not reversible is called irreversible. This concept arises frequently in thermodynamics. All complex natural processes are irreversible, although a phase transition at the coexistence temperature (e.g. melting of i ...
* Magnetic catalysis of chiral symmetry breaking
* Mermin–Wagner theorem
In quantum field theory and statistical mechanics, the Mermin–Wagner theorem (also known as Mermin–Wagner–Hohenberg theorem, Mermin–Wagner–Berezinskii theorem, or Coleman theorem) states that continuous symmetries cannot be spontaneously ...
* Norton's dome
Norton's dome is a thought experiment that exhibits a non-deterministic system within the bounds of Newtonian mechanics. It was devised by John D. Norton in 2003. It is a special limiting case of a more general class of examples from 1997 due t ...
* Second-order phase transition
In chemistry, thermodynamics, and other related fields, a phase transition (or phase change) is the physical process of transition between one state of a medium and another. Commonly the term is used to refer to changes among the basic states o ...
* Spontaneous absolute asymmetric synthesis in chemistry
* Symmetry breaking
In physics, symmetry breaking is a phenomenon in which (infinitesimally) small fluctuations acting on a system crossing a critical point decide the system's fate, by determining which branch of a bifurcation is taken. To an outside observe ...
* Tachyon condensation
A tachyon () or tachyonic particle is a hypothetical particle that always travels faster than light. Physicists believe that faster-than-light particles cannot exist because they are not consistent with the known laws of physics. If such parti ...
* 1964 PRL symmetry breaking papers
The 1964 ''PRL'' symmetry breaking papers were written by three teams who proposed related but different approaches to explain how mass could arise in local gauge theory, gauge theories. These three papers were written by: Robert Brout and Franço ...
Notes
* Note that (as in fundamental Higgs driven spontaneous gauge symmetry breaking) the term "symmetry breaking" is a misnomer when applied to gauge symmetries.References
External links
* For a pedagogic introduction to electroweak symmetry breaking with step by step derivations, not found in texts, of many key relations, see http://www.quantumfieldtheory.info/Electroweak_Sym_breaking.pdfSpontaneous symmetry breaking
Physical Review Letters – 50th Anniversary Milestone Papers
In CERN Courier, Steven Weinberg reflects on spontaneous symmetry breaking
Englert–Brout–Higgs–Guralnik–Hagen–Kibble Mechanism on Scholarpedia
History of Englert–Brout–Higgs–Guralnik–Hagen–Kibble Mechanism on Scholarpedia
The History of the Guralnik, Hagen and Kibble development of the Theory of Spontaneous Symmetry Breaking and Gauge Particles
* [http://www.datafilehost.com/download-7d512618.html Guralnik, G S; Hagen, C R and Kibble, T W B (1967). Broken Symmetries and the Goldstone Theorem. Advances in Physics, vol. 2 Interscience Publishers, New York. pp. 567–708]
Spontaneous Symmetry Breaking in Gauge Theories: a Historical Survey
{{DEFAULTSORT:Spontaneous Symmetry Breaking Theoretical physics Quantum field theory Standard Model Quantum chromodynamics Symmetry Quantum phases