Solenoid (mathematics) on:
[Wikipedia]
[Google]
[Amazon]
:''This page discusses a class of topological groups. For the wrapped loop of wire, see  In
In

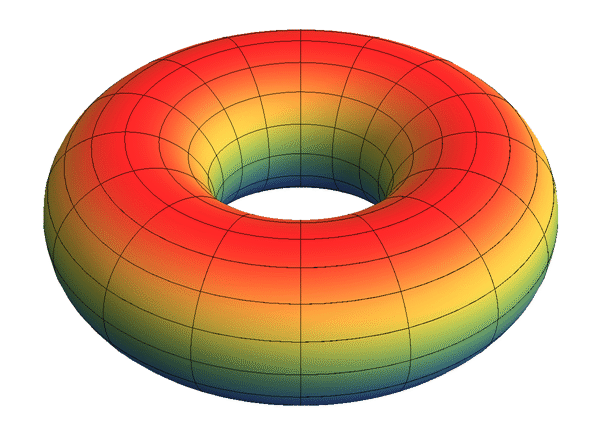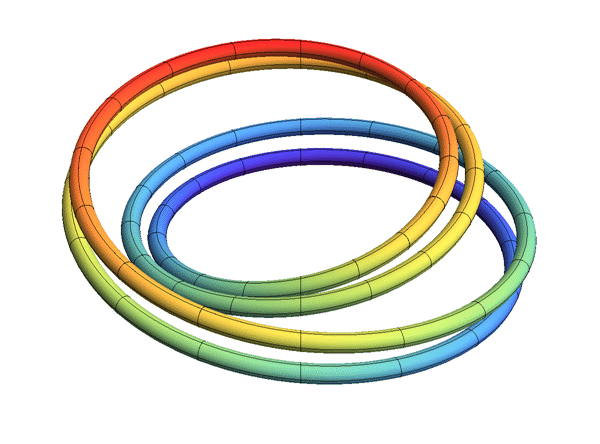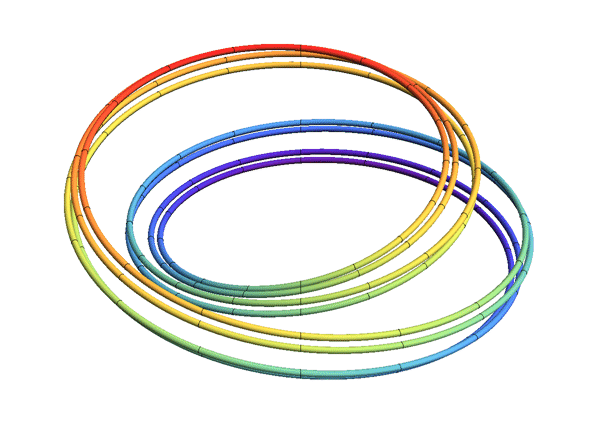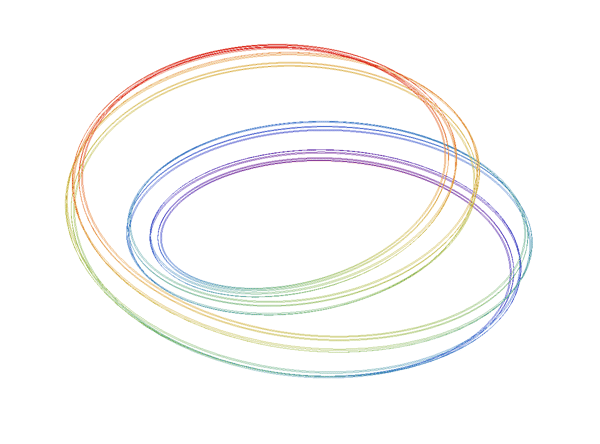 Each solenoid may be constructed as the intersection of a nested system of embedded solid tori in R3.
Fix a sequence of natural numbers , ''n''''i'' ≥ 2. Let ''T''0 = ''S''1 × ''D'' be a solid torus. For each ''i'' ≥ 0, choose a solid torus ''T''''i''+1 that is wrapped longitudinally ''n''''i'' times inside the solid torus ''T''''i''. Then their intersection
:
is
Each solenoid may be constructed as the intersection of a nested system of embedded solid tori in R3.
Fix a sequence of natural numbers , ''n''''i'' ≥ 2. Let ''T''0 = ''S''1 × ''D'' be a solid torus. For each ''i'' ≥ 0, choose a solid torus ''T''''i''+1 that is wrapped longitudinally ''n''''i'' times inside the solid torus ''T''''i''. Then their intersection
:
is
''Differentiable dynamical systems''
Bull. of the AMS, 73 (1967), 747 – 817. * L. Vietoris, ''├£ber den h├Čheren Zusammenhang kompakter R├żume und eine Klasse von zusammenhangstreuen Abbildungen'', Math. Ann. 97 (1927), pp. 454ŌĆō472 * Robert F. Williams
''Expanding attractors''
Publ. Math. IH├ēS, t. 43 (1974), p. 169ŌĆō203
Solenoid
upright=1.20, An illustration of a solenoid
upright=1.20, Magnetic field created by a seven-loop solenoid (cross-sectional view) described using field lines
A solenoid () is a type of electromagnet formed by a helix, helical coil of wire whos ...
.''
 In
In mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, a solenoid is a compact
Compact as used in politics may refer broadly to a pact or treaty; in more specific cases it may refer to:
* Interstate compact, a type of agreement used by U.S. states
* Blood compact, an ancient ritual of the Philippines
* Compact government, a t ...
connected topological space
In mathematics, a topological space is, roughly speaking, a Geometry, geometrical space in which Closeness (mathematics), closeness is defined but cannot necessarily be measured by a numeric Distance (mathematics), distance. More specifically, a to ...
(i.e. a continuum) that may be obtained as the inverse limit
In mathematics, the inverse limit (also called the projective limit) is a construction that allows one to "glue together" several related objects, the precise gluing process being specified by morphisms between the objects. Thus, inverse limits ca ...
of an inverse system of topological group
In mathematics, topological groups are the combination of groups and topological spaces, i.e. they are groups and topological spaces at the same time, such that the continuity condition for the group operations connects these two structures ...
s and continuous homomorphism
In algebra, a homomorphism is a morphism, structure-preserving map (mathematics), map between two algebraic structures of the same type (such as two group (mathematics), groups, two ring (mathematics), rings, or two vector spaces). The word ''homo ...
s
:
where each is a circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
and ''f''''i'' is the map that uniformly wraps the circle for times () around the circle .
This construction can be carried out geometrically in the three-dimensional Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
R3. A solenoid is a one-dimensional homogeneous indecomposable continuum that has the structure of an abelian compact topological group
In mathematics, topological groups are the combination of groups and topological spaces, i.e. they are groups and topological spaces at the same time, such that the continuity condition for the group operations connects these two structures ...
.
Solenoids were first introduced by Vietoris for the case, and by van Dantzig the case, where is fixed. Such a solenoid arises as a one-dimensional expanding attractor, or SmaleŌĆōWilliams attractor, and forms an important example in the theory of hyperbolic
Hyperbolic may refer to:
* of or pertaining to a hyperbola, a type of smooth curve lying in a plane in mathematics
** Hyperbolic geometry, a non-Euclidean geometry
** Hyperbolic functions, analogues of ordinary trigonometric functions, defined u ...
dynamical system
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space, such as in a parametric curve. Examples include the mathematical models ...
s.
Construction
Geometric construction and the SmaleŌĆōWilliams attractor

 Each solenoid may be constructed as the intersection of a nested system of embedded solid tori in R3.
Fix a sequence of natural numbers , ''n''''i'' ≥ 2. Let ''T''0 = ''S''1 × ''D'' be a solid torus. For each ''i'' ≥ 0, choose a solid torus ''T''''i''+1 that is wrapped longitudinally ''n''''i'' times inside the solid torus ''T''''i''. Then their intersection
:
is
Each solenoid may be constructed as the intersection of a nested system of embedded solid tori in R3.
Fix a sequence of natural numbers , ''n''''i'' ≥ 2. Let ''T''0 = ''S''1 × ''D'' be a solid torus. For each ''i'' ≥ 0, choose a solid torus ''T''''i''+1 that is wrapped longitudinally ''n''''i'' times inside the solid torus ''T''''i''. Then their intersection
:
is homeomorphic
In mathematics and more specifically in topology, a homeomorphism ( from Greek roots meaning "similar shape", named by Henri Poincar├®), also called topological isomorphism, or bicontinuous function, is a bijective and continuous function betw ...
to the solenoid constructed as the inverse limit of the system of circles with the maps determined by the sequence .
Here is a variant of this construction isolated by Stephen Smale as an example of an expanding attractor in the theory of smooth dynamical systems. Denote the angular coordinate on the circle ''S''1 by ''t'' (it is defined mod 2π) and consider the complex coordinate ''z'' on the two-dimensional unit disk
In mathematics, the open unit disk (or disc) around ''P'' (where ''P'' is a given point in the plane), is the set of points whose distance from ''P'' is less than 1:
:D_1(P) = \.\,
The closed unit disk around ''P'' is the set of points whose d ...
''D''. Let ''f'' be the map of the solid torus ''T'' = ''S''1 × ''D'' into itself given by the explicit formula
:
This map is a smooth embedding
In mathematics, an embedding (or imbedding) is one instance of some mathematical structure contained within another instance, such as a group (mathematics), group that is a subgroup.
When some object X is said to be embedded in another object Y ...
of ''T'' into itself that preserves the foliation
In mathematics (differential geometry), a foliation is an equivalence relation on an topological manifold, ''n''-manifold, the equivalence classes being connected, injective function, injectively immersed submanifolds, all of the same dimension ...
by meridional disks (the constants 1/2 and 1/4 are somewhat arbitrary, but it is essential that 1/4 < 1/2 and 1/4 + 1/2 < 1). If ''T'' is imagined as a rubber tube, the map ''f'' stretches it in the longitudinal direction, contracts each meridional disk, and wraps the deformed tube twice inside ''T'' with twisting, but without self-intersections. The hyperbolic set ''Λ'' of the discrete dynamical system (''T'', ''f'') is the intersection of the sequence of nested solid tori described above, where ''T''''i'' is the image of ''T'' under the ''i''th iteration of the map ''f''. This set is a one-dimensional (in the sense of topological dimension) attractor, and the dynamics of ''f'' on ''Λ'' has the following interesting properties:
* meridional disks are the stable manifolds, each of which intersects ''Λ'' over a Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of unintuitive properties. It was discovered in 1874 by Henry John Stephen Smith and mentioned by German mathematician Georg Cantor in 1883.
Throu ...
* periodic point
In mathematics, in the study of iterated functions and dynamical systems, a periodic point of a function (mathematics), function is a point which the system returns to after a certain number of function iterations or a certain amount of time.
It ...
s of ''f'' are dense
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''Žü'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be use ...
in ''Λ''
* the map ''f'' is topologically transitive on ''Λ''
General theory of solenoids and expanding attractors, not necessarily one-dimensional, was developed by R. F. Williams and involves a projective system of infinitely many copies of a compact branched manifold in place of the circle, together with an expanding self-immersion
Immersion may refer to:
The arts
* "Immersion", a 2012 story by Aliette de Bodard
* ''Immersion'', a French comic book series by L├®o Quievreux
* ''Immersion'' (album), the third album by Australian group Pendulum
* ''Immersion'' (film), a 2021 ...
.
Construction in toroidal coordinates
In thetoroidal coordinates
Toroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional bipolar coordinate system about the axis that separates its two foci. Thus, the two foci F_1 and F_2 in bipolar coordinate ...
with radius , the solenoid can be parametrized by aswhere
Here, are adjustable shape-parameters, with constraint . In particular, works.
Let be the solenoid constructed this way, then the topology of the solenoid is just the subset topology induced by the Euclidean topology
In mathematics, and especially general topology, the Euclidean topology is the natural topology induced on n-dimensional Euclidean space \R^n by the Euclidean metric.
Definition
The Euclidean norm on \R^n is the non-negative function \, \cdot ...
on .
Since the parametrization is bijective, we can pullback the topology on to , which makes itself the solenoid. This allows us to construct the inverse limit maps explicitly:
Construction by symbolic dynamics
Viewed as a set, the solenoid is just a Cantor-continuum of circles, wired together in a particular way. This suggests to us the construction bysymbolic dynamics
In mathematics, symbolic dynamics is the study of dynamical systems defined on a discrete space consisting of infinite sequences of abstract symbols. The evolution of the dynamical system is defined as a simple shift of the sequence.
Because of t ...
, where we start with a circle as a "racetrack", and append an "odometer" to keep track of which circle we are on.
Define as the solenoid. Next, define addition on the odometer , in the same way as ''p''-adic numbers.
Next, define addition on the solenoid byThe topology on the solenoid is generated by the basis containing the subsets , where is any open interval in , and is the set of all elements of starting with the initial segment .
Pathological properties
Solenoids arecompact
Compact as used in politics may refer broadly to a pact or treaty; in more specific cases it may refer to:
* Interstate compact, a type of agreement used by U.S. states
* Blood compact, an ancient ritual of the Philippines
* Compact government, a t ...
metrizable space
In topology and related areas of mathematics, a metrizable space is a topological space that is Homeomorphism, homeomorphic to a metric space. That is, a topological space (X, \tau) is said to be metrizable if there is a Metric (mathematics), metr ...
s that are connected, but not locally connected
In topology and other branches of mathematics, a topological space ''X'' is
locally connected if every point admits a neighbourhood basis consisting of open connected sets.
As a stronger notion, the space ''X'' is locally path connected if ev ...
or path connected
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union (set theory), union of two or more disjoint set, disjoint Empty set, non-empty open (topology), open subsets. Conne ...
. This is reflected in their pathological
Pathology is the study of disease. The word ''pathology'' also refers to the study of disease in general, incorporating a wide range of biology research fields and medical practices. However, when used in the context of modern medical treatme ...
behavior with respect to various homology theories
In mathematics, the term homology, originally introduced in algebraic topology, has three primary, closely-related usages. The most direct usage of the term is to take the ''homology of a chain complex'', resulting in a sequence of abelian group ...
, in contrast with the standard properties of homology for simplicial complex
In mathematics, a simplicial complex is a structured Set (mathematics), set composed of Point (geometry), points, line segments, triangles, and their ''n''-dimensional counterparts, called Simplex, simplices, such that all the faces and intersec ...
es. In ─īech homology, one can construct a non-exact long homology sequence using a solenoid. In Steenrod-style homology theories, the 0th homology group of a solenoid may have a fairly complicated structure, even though a solenoid is a connected space.
See also
*Protorus
In mathematics, a protorus is a compact space, compact connected space, connected topological abelian group. Equivalently, it is a projective limit of torus, tori (products of a finite number of copies of the circle group), or the Pontryagin dual o ...
, a class of topological groups that includes the solenoids
*Pontryagin duality
In mathematics, Pontryagin duality is a duality between locally compact abelian groups that allows generalizing Fourier transform to all such groups, which include the circle group (the multiplicative group of complex numbers of modulus one), ...
* ''p''-adic solenoid
*Profinite integer
In mathematics, a profinite integer is an element of the ring (mathematics), ring (sometimes pronounced as zee-hat or zed-hat)
:\widehat = \varprojlim \mathbb/n\mathbb,
where the inverse limit of the quotient rings \mathbb/n\mathbb runs through al ...
References
* D. van Dantzig, ''Ueber topologisch homogene Kontinua'', Fund. Math. 15 (1930), pp. 102ŌĆō125 * * Clark Robinson, ''Dynamical systems: Stability, Symbolic Dynamics and Chaos'', 2nd edition, CRC Press, 1998 * S. Smale''Differentiable dynamical systems''
Bull. of the AMS, 73 (1967), 747 – 817. * L. Vietoris, ''├£ber den h├Čheren Zusammenhang kompakter R├żume und eine Klasse von zusammenhangstreuen Abbildungen'', Math. Ann. 97 (1927), pp. 454ŌĆō472 * Robert F. Williams
''Expanding attractors''
Publ. Math. IH├ēS, t. 43 (1974), p. 169ŌĆō203
Further reading
* {{DEFAULTSORT:Solenoid (Mathematics) Topological groups Continuum theory Algebraic topology Ring theory Number theory P-adic numbers