Snowdrift Game on:
[Wikipedia]
[Google]
[Amazon]
The game of chicken, also known as the hawk–dove game or snowdrift game, is a model of conflict for two players in game theory. The principle of the game is that while the ideal outcome is for one player to yield (to avoid the worst outcome if neither yields), the individuals try to avoid it out of pride for not wanting to look like a "chicken". Each player taunts the other to increase the risk of shame in yielding. However, when one player yields, the conflict is avoided, and the game is for the most part over.
The name "chicken" has its origins in a game in which two drivers drive toward each other on a collision course: one must swerve, or both may die in the crash, but if one driver swerves and the other does not, the one who swerved will be called a "
 The exact value of the Dove vs. Dove payoff varies between model formulations. Sometimes the players are assumed to split the payoff equally (V/2 each), other times the payoff is assumed to be zero (since this is the expected payoff to a
The exact value of the Dove vs. Dove payoff varies between model formulations. Sometimes the players are assumed to split the payoff equally (V/2 each), other times the payoff is assumed to be zero (since this is the expected payoff to a
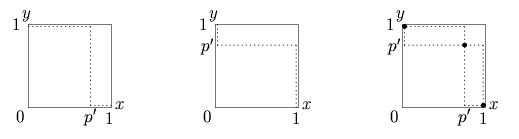 All anti-coordination games have three
All anti-coordination games have three

 The single population model presents a situation where no uncorrelated asymmetries exist, and so the best players can do is randomize their strategies. The two population models provide such an asymmetry and the members of each population will then use that to correlate their strategies. In the two population model, one population gains at the expense of another. Hawk–Dove and Chicken thus illustrate an interesting case where the qualitative results for the two different versions of the replicator dynamics differ wildly.
The single population model presents a situation where no uncorrelated asymmetries exist, and so the best players can do is randomize their strategies. The two population models provide such an asymmetry and the members of each population will then use that to correlate their strategies. In the two population model, one population gains at the expense of another. Hawk–Dove and Chicken thus illustrate an interesting case where the qualitative results for the two different versions of the replicator dynamics differ wildly.
The game of Chicken as a metaphor for human conflict
Game of Chicken – Rebel Without a Cause
by Elmer G. Wiens.
Online model: Expected Dynamics of an Imitation Model in the Hawk-Dove Game
Online model: Expected Dynamics of an Intra-Population Imitation Model in the Two-Population Hawk-Dove Game
{{Game theory Non-cooperative games Evolutionary game theory Endurance games Social science experiments
chicken
The chicken (''Gallus gallus domesticus'') is a domestication, domesticated junglefowl species, with attributes of wild species such as the grey junglefowl, grey and the Ceylon junglefowl that are originally from Southeastern Asia. Rooster ...
", meaning a coward; this terminology is most prevalent in political science
Political science is the scientific study of politics. It is a social science dealing with systems of governance and power, and the analysis of political activities, political thought, political behavior, and associated constitutions and ...
and economics
Economics () is the social science that studies the production, distribution, and consumption of goods and services.
Economics focuses on the behaviour and interactions of economic agents and how economies work. Microeconomics analy ...
. The name "hawk–dove" refers to a situation in which there is a competition for a shared resource and the contestants can choose either conciliation or conflict; this terminology is most commonly used in biology
Biology is the scientific study of life. It is a natural science with a broad scope but has several unifying themes that tie it together as a single, coherent field. For instance, all organisms are made up of cells that process hereditar ...
and evolutionary game theory
Evolutionary game theory (EGT) is the application of game theory to evolving populations in biology. It defines a framework of contests, strategies, and analytics into which Darwinian competition can be modelled. It originated in 1973 with John Ma ...
. From a game-theoretic point of view, "chicken" and "hawk–dove" are identical. The game has also been used to describe the mutual assured destruction
Mutual assured destruction (MAD) is a doctrine of military strategy and national security policy which posits that a full-scale use of nuclear weapons by an attacker on a nuclear-armed defender with second-strike capabilities would cause the ...
of nuclear warfare
Nuclear warfare, also known as atomic warfare, is a theoretical military conflict or prepared political strategy that deploys nuclear weaponry. Nuclear weapons are weapons of mass destruction; in contrast to conventional warfare, nucle ...
, especially the sort of brinkmanship involved in the Cuban Missile Crisis
The Cuban Missile Crisis, also known as the October Crisis (of 1962) ( es, Crisis de Octubre) in Cuba, the Caribbean Crisis () in Russia, or the Missile Scare, was a 35-day (16 October – 20 November 1962) confrontation between the Unite ...
.Russell (1959) p. 30.
Popular versions
The game of chicken models two drivers, both headed for a single-lane bridge from opposite directions. The first to swerve away yields the bridge to the other. If neither player swerves, the result is a costly deadlock in the middle of the bridge, or a potentially fatal head-on collision. It is presumed that the best thing for each driver is to stay straight while the other swerves (since the other is the "chicken" while a crash is avoided). Additionally, a crash is presumed to be the worst outcome for both players. This yields a situation where each player, in attempting to secure their best outcome, risks the worst. The phrase ''game of chicken'' is also used as a metaphor for a situation where two parties engage in a showdown where they have nothing to gain, and only pride stops them from backing down.Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, (18 May 1872 – 2 February 1970) was a British mathematician, philosopher, logician, and public intellectual. He had a considerable influence on mathematics, logic, set theory, linguistics, ar ...
famously compared the game of Chicken to nuclear
Nuclear may refer to:
Physics
Relating to the nucleus of the atom:
*Nuclear engineering
*Nuclear physics
*Nuclear power
*Nuclear reactor
*Nuclear weapon
*Nuclear medicine
*Radiation therapy
*Nuclear warfare
Mathematics
*Nuclear space
* Nuclear ...
brinkmanship:
Since the nuclear stalemate became apparent, the Governments of East and West have adopted the policy which Mr. Dulles calls 'brinkmanship'. This is a policy adapted from a sport which, I am told, is practiced by some youthful degenerates. This sport is called 'Chicken!'. It is played by choosing a long straight road with a white line down the middle and starting two very fast cars toward each other from opposite ends. Each car is expected to keep the wheels on one side of the white line. As they approach each other, mutual destruction becomes more and more imminent. If one of them swerves from the white line before the other, the other, as they pass, shouts 'Chicken!', and the one who has swerved becomes an object of contempt. As played by irresponsible boys, this game is considered decadent and immoral, though only the lives of the players are risked. But when the game is played by eminent statesmen, who risk not only their own lives but those of many hundreds of millions of human beings, it is thought on both sides that the statesmen on one side are displaying a high degree of wisdom and courage, and only the statesmen on the other side are reprehensible. This, of course, is absurd. Both are to blame for playing such an incredibly dangerous game. The game may be played without misfortune a few times, but sooner or later it will come to be felt that loss of face is more dreadful than nuclear annihilation. The moment will come when neither side can face the derisive cry of 'Chicken!' from the other side. When that moment is come, the statesmen of both sides will plunge the world into destruction.Brinkmanship involves the introduction of an element of uncontrollable risk: even if all players act rationally in the face of risk, uncontrollable events can still trigger the catastrophic outcome.Dixit and Nalebuff (1991) pp. 205–222. In the "chickie run" scene from the film ''
Rebel Without a Cause
''Rebel Without a Cause'' is a 1955 American coming-of-age drama film about emotionally confused suburban
A suburb (more broadly suburban area) is an area within a metropolitan area, which may include commercial and mixed-use, that ...
'', this happens when Buzz cannot escape from the car and dies in the crash. The opposite scenario occurs in '' Footloose'' where Ren McCormack is stuck in his tractor and hence wins the game as they cannot play "chicken". A similar event happens in two different games in the film '' The Heavenly Kid'', when first Bobby, and then later Lenny become stuck in their cars and drive off a cliff. The basic game-theoretic formulation of Chicken has no element of variable, potentially catastrophic, risk, and is also the contraction of a dynamic situation into a one-shot interaction.
The hawk–dove version of the game imagines two players (animals) contesting an indivisible resource who can choose between two strategies, one more escalated than the other. They can use threat displays (play Dove), or physically attack each other (play Hawk). If both players choose the Hawk strategy, then they fight until one is injured and the other wins. If only one player chooses Hawk, then this player defeats the Dove player. If both players play Dove, there is a tie, and each player receives a payoff lower than the profit of a hawk defeating a dove.
Game theoretic applications
Chicken
A formal version of the game of Chicken has been the subject of serious research in game theory. Two versions of thepayoff matrix
In game theory, normal form is a description of a ''game''. Unlike extensive form, normal-form representations are not graphical ''per se'', but rather represent the game by way of a matrix. While this approach can be of greater use in identifyin ...
for this game are presented here (Figures 1 and 2). In Figure 1, the outcomes are represented in words, where each player would prefer to win over tying, prefer to tie over losing, and prefer to lose over crashing. Figure 2 presents arbitrarily set numerical payoffs which theoretically conform to this situation. Here, the benefit of winning is 1, the cost of losing is -1, and the cost of crashing is -1000.
Both Chicken and Hawk–Dove are ''anti-coordination games'', in which it is mutually beneficial for the players to play different strategies. In this way, it can be thought of as the opposite of a coordination game A coordination game is a type of simultaneous game found in game theory. It describes the situation where a player will earn a higher payoff when they select the same course of action as another player. The game is not one of pure conflict, which r ...
, where playing the same strategy Pareto dominates playing different strategies. The underlying concept is that players use a shared resource. In coordination games, sharing the resource creates a benefit for all: the resource is non-rivalrous, and the shared usage creates positive externalities
In economics, an externality or external cost is an indirect cost or benefit to an uninvolved third party that arises as an effect of another party's (or parties') activity. Externalities can be considered as unpriced goods involved in either co ...
. In anti-coordination games the resource is rivalrous but non-excludable
In economics, a good, service or resource are broadly assigned two fundamental characteristics; a degree of excludability and a degree of rivalry. Excludability is defined as the degree to which a good, service or resource can be limited to only p ...
and sharing comes at a cost (or negative externality).
Because the loss of swerving is so trivial compared to the crash that occurs if nobody swerves, the reasonable strategy would seem to be to swerve before a crash is likely. Yet, knowing this, if one believes one's opponent to be reasonable, one may well decide not to swerve at all, in the belief that the opponent will be reasonable and decide to swerve, leaving the first player the winner. This unstable situation can be formalized by saying there is more than one Nash equilibrium
In game theory, the Nash equilibrium, named after the mathematician John Nash, is the most common way to define the solution of a non-cooperative game involving two or more players. In a Nash equilibrium, each player is assumed to know the equ ...
, which is a pair of strategies for which neither player gains by changing their own strategy while the other stays the same. (In this case, the pure strategy equilibria are the two situations wherein one player swerves while the other does not.)
Hawk–dove
In the biological literature, this game is known as Hawk–Dove. The earliest presentation of a form of the Hawk–Dove game was byJohn Maynard Smith
John Maynard Smith (6 January 1920 – 19 April 2004) was a British theoretical and mathematical evolutionary biologist and geneticist. Originally an aeronautical engineer during the Second World War, he took a second degree in genetics ...
and George Price George Price may refer to:
* George Price (footballer) (c. 1878–1938), footballer
* George Price (cartoonist) (1901–1995), American cartoonist
* George Cadle Price (1919–2011), prime minister of Belize
* George E. Price (1848–1938), member ...
in their paper, "The logic of animal conflict". The traditional payoff matrix
In game theory, normal form is a description of a ''game''. Unlike extensive form, normal-form representations are not graphical ''per se'', but rather represent the game by way of a matrix. While this approach can be of greater use in identifyin ...
for the Hawk–Dove game is given in Figure 3, where V is the value of the contested resource, and C is the cost of an escalated fight. It is (almost always) assumed that the value of the resource is less than the cost of a fight, i.e., C > V > 0. If C ≤ V, the resulting game is not a game of Chicken but is instead a Prisoner's Dilemma
The Prisoner's Dilemma is an example of a game analyzed in game theory. It is also a thought experiment that challenges two completely rational agents to a dilemma: cooperate with their partner for mutual reward, or betray their partner ("de ...
.
 The exact value of the Dove vs. Dove payoff varies between model formulations. Sometimes the players are assumed to split the payoff equally (V/2 each), other times the payoff is assumed to be zero (since this is the expected payoff to a
The exact value of the Dove vs. Dove payoff varies between model formulations. Sometimes the players are assumed to split the payoff equally (V/2 each), other times the payoff is assumed to be zero (since this is the expected payoff to a war of attrition
The War of Attrition ( ar, حرب الاستنزاف, Ḥarb al-Istinzāf; he, מלחמת ההתשה, Milhemet haHatashah) involved fighting between Israel and Egypt, Jordan, the Palestine Liberation Organisation (PLO) and their allies from ...
game, which is the presumed models for a contest decided by display duration).
While the Hawk–Dove game is typically taught and discussed with the payoffs in terms of V and C, the solutions hold true for any matrix with the payoffs in Figure 4, where W > T > L > X.
Hawk–dove variants
Biologists have explored modified versions of classic Hawk–Dove game to investigate a number of biologically relevant factors. These include adding variation in resource holding potential, and differences in the value of winning to the different players, allowing the players to threaten each other before choosing moves in the game,Kim (1995). and extending the interaction to two plays of the game.Pre-commitment
One tactic in the game is for one party to signal their intentions convincingly before the game begins. For example, if one party were to ostentatiously disable their steering wheel just before the match, the other party would be compelled to swerve. This shows that, in some circumstances, reducing one's own options can be a good strategy. One real-world example is a protester who handcuffs themselves to an object, so that no threat can be made which would compel them to move (since they cannot move). Another example, taken from fiction, is found inStanley Kubrick
Stanley Kubrick (; July 26, 1928 – March 7, 1999) was an American film director, producer, screenwriter, and photographer. Widely considered one of the greatest filmmakers of all time, his films, almost all of which are adaptations of nove ...
's ''Dr. Strangelove
''Dr. Strangelove or: How I Learned to Stop Worrying and Love the Bomb'', known simply and more commonly as ''Dr. Strangelove'', is a 1964 black comedy film that satirizes the Cold War fears of a nuclear conflict between the Soviet Union and t ...
''. In that film, the Russians
, native_name_lang = ru
, image =
, caption =
, population =
, popplace =
118 million Russians in the Russian Federation (2002 ''Winkler Prins'' estimate)
, region1 =
, pop1 ...
sought to deter American attack by building a "doomsday machine", a device that would trigger world annihilation if Russia was hit by nuclear weapons or if any attempt were made to disarm it. However, the Russians had planned to signal the deployment of the machine a few days after having set it up, which, because of an unfortunate course of events, turned out to be too late.
Players may also make non-binding threats to not swerve. This has been modeled explicitly in the Hawk–Dove game. Such threats work, but must be wastefully costly if the threat is one of two possible signals ("I will not swerve" or "I will swerve"), or they will be costless if there are three or more signals (in which case the signals will function as a game of "rock, paper, scissors
Rock paper scissors (also known by other orderings of the three items, with "rock" sometimes being called "stone," or as Rochambeau, roshambo, or ro-sham-bo) is a hand game originating in China, usually played between two people, in which each ...
").
Best response mapping and Nash equilibria
 All anti-coordination games have three
All anti-coordination games have three Nash equilibria
In game theory, the Nash equilibrium, named after the mathematician John Nash, is the most common way to define the solution of a non-cooperative game involving two or more players. In a Nash equilibrium, each player is assumed to know the equ ...
. Two of these are pure contingent strategy profiles, in which each player plays one of the pair of strategies, and the other player chooses the opposite strategy. The third one is a mixed equilibrium, in which each player probabilistically chooses between the two pure strategies. Either the pure, or mixed, Nash equilibria will be evolutionarily stable strategies
An evolutionarily stable strategy (ESS) is a strategy (or set of strategies) that is ''impermeable'' when adopted by a population in adaptation to a specific environment, that is to say it cannot be displaced by an alternative strategy (or set of ...
depending upon whether uncorrelated asymmetries exist.
The best response
In game theory, the best response is the strategy (or strategies) which produces the most favorable outcome for a player, taking other players' strategies as given (; ). The concept of a best response is central to John Nash's best-known contribu ...
mapping for all 2x2 anti-coordination games is shown in Figure 5. The variables ''x'' and ''y'' in Figure 5 are the probabilities of playing the escalated strategy ("Hawk" or "Don't swerve") for players X and Y respectively. The line in graph on the left shows the optimum probability of playing the escalated strategy for player Y as a function of ''x''. The line in the second graph shows the optimum probability of playing the escalated strategy for player X as a function of ''y'' (the axes have not been rotated, so the dependent variable
Dependent and independent variables are variables in mathematical modeling, statistical modeling and experimental sciences. Dependent variables receive this name because, in an experiment, their values are studied under the supposition or dema ...
is plotted on the abscissa
In common usage, the abscissa refers to the (''x'') coordinate and the ordinate refers to the (''y'') coordinate of a standard two-dimensional graph.
The distance of a point from the y-axis, scaled with the x-axis, is called abscissa or x coo ...
, and the independent variable
Dependent and independent variables are variables in mathematical modeling, statistical modeling and experimental sciences. Dependent variables receive this name because, in an experiment, their values are studied under the supposition or deman ...
is plotted on the ordinate
In common usage, the abscissa refers to the (''x'') coordinate and the ordinate refers to the (''y'') coordinate of a standard two-dimensional graph.
The distance of a point from the y-axis, scaled with the x-axis, is called abscissa or x coo ...
). The Nash equilibria are where the players' correspondences agree, i.e., cross. These are shown with points in the right hand graph. The best response mappings agree (i.e., cross) at three points. The first two Nash equilibria are in the top left and bottom right corners, where one player chooses one strategy, the other player chooses the opposite strategy. The third Nash equilibrium is a mixed strategy which lies along the diagonal from the bottom left to top right corners. If the players do not know which one of them is which, then the mixed Nash is an evolutionarily stable strategy
An evolutionarily stable strategy (ESS) is a strategy (or set of strategies) that is ''impermeable'' when adopted by a population in adaptation to a specific environment, that is to say it cannot be displaced by an alternative strategy (or set o ...
(ESS), as play is confined to the bottom left to top right diagonal line. Otherwise an uncorrelated asymmetry is said to exist, and the corner Nash equilibria are ESSes.
Strategy polymorphism vs strategy mixing
The ESS for the Hawk–Dove game is a mixed strategy. Formal game theory is indifferent to whether this mixture is due to all players in a population choosing randomly between the two pure strategies (a range of possible instinctive reactions for a single situation) or whether the population is a polymorphic mixture of players dedicated to choosing a particular pure strategy(a single reaction differing from individual to individual). Biologically, these two options are strikingly different ideas. The Hawk–Dove game has been used as a basis for evolutionary simulations to explore which of these two modes of mixing ought to predominate in reality.Symmetry breaking
In both "Chicken" and "Hawk–Dove", the onlysymmetric
Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definit ...
Nash equilibrium
In game theory, the Nash equilibrium, named after the mathematician John Nash, is the most common way to define the solution of a non-cooperative game involving two or more players. In a Nash equilibrium, each player is assumed to know the equ ...
is the mixed strategy
In game theory, a player's strategy is any of the options which they choose in a setting where the outcome depends ''not only'' on their own actions ''but'' on the actions of others. The discipline mainly concerns the action of a player in a game ...
Nash equilibrium, where both individuals randomly chose between playing Hawk/Straight or Dove/Swerve. This mixed strategy equilibrium is often sub-optimal—both players would do better if they could coordinate their actions in some way. This observation has been made independently in two different contexts, with almost identical results.Skyrms (1996) pp. 76–79.
Correlated equilibrium and the game of chicken
Consider the version of "Chicken" pictured in Figure 6. Like all forms of the game, there are threeNash equilibria
In game theory, the Nash equilibrium, named after the mathematician John Nash, is the most common way to define the solution of a non-cooperative game involving two or more players. In a Nash equilibrium, each player is assumed to know the equ ...
. The two pure strategy Nash equilibria are (''D'', ''C'') and (''C'', ''D''). There is also a mixed strategy
In game theory, a player's strategy is any of the options which they choose in a setting where the outcome depends ''not only'' on their own actions ''but'' on the actions of others. The discipline mainly concerns the action of a player in a game ...
equilibrium where each player Dares with probability 1/3. It results in expected payoffs of 14/3 = 4.667 for each player.
Now consider a third party (or some natural event) that draws one of three cards labeled: (''C'', ''C''), (''D'', ''C''), and (''C'', ''D''). This exogenous draw event is assumed to be uniformly at random over the 3 outcomes. After drawing the card the third party informs the players of the strategy assigned to them on the card (but not the strategy assigned to their opponent). Suppose a player is assigned ''D'', they would not want to deviate supposing the other player played their assigned strategy since they will get 7 (the highest payoff possible). Suppose a player is assigned ''C''. Then the other player has been assigned ''C'' with probability 1/2 and ''D'' with probability 1/2 (due to the nature of the exogenous draw). The expected utility The expected utility hypothesis is a popular concept in economics that serves as a reference guide for decisions when the payoff is uncertain. The theory recommends which option rational individuals should choose in a complex situation, based on the ...
of Daring is 0(1/2) + 7(1/2) = 3.5 and the expected utility of chickening out is 2(1/2) + 6(1/2) = 4. So, the player would prefer to chicken out.
Since neither player has an incentive to deviate from the drawn assignments, this probability distribution over the strategies is known as a correlated equilibrium
In game theory, a correlated equilibrium is a solution concept that is more general than the well known Nash equilibrium. It was first discussed by mathematician Robert Aumann in 1974. The idea is that each player chooses their action accordin ...
of the game. Notably, the expected payoff for this equilibrium is 7(1/3) + 2(1/3) + 6(1/3) = 5 which is higher than the expected payoff of the mixed strategy Nash equilibrium.
Uncorrelated asymmetries and solutions to the hawk–dove game
Although there are three Nash equilibria in the Hawk–Dove game, the one which emerges as theevolutionarily stable strategy
An evolutionarily stable strategy (ESS) is a strategy (or set of strategies) that is ''impermeable'' when adopted by a population in adaptation to a specific environment, that is to say it cannot be displaced by an alternative strategy (or set o ...
(ESS) depends upon the existence of any uncorrelated asymmetry In game theory an uncorrelated asymmetry is an arbitrary asymmetry in a game which is otherwise symmetrical. The name 'uncorrelated asymmetry' is due to John Maynard Smith who called payoff relevant asymmetries in games with similar roles for eac ...
in the game (in the sense of anti-coordination games). In order for row players to choose one strategy and column players the other, the players must be able to distinguish which role (column or row player) they have. If no such uncorrelated asymmetry exists then both players must choose the same strategy, and the ESS will be the mixing Nash equilibrium. If there is an uncorrelated asymmetry, then the mixing Nash is not an ESS, but the two pure, role contingent, Nash equilibria are.
The standard biological interpretation of this uncorrelated asymmetry is that one player is the territory owner, while the other is an intruder on the territory. In most cases, the territory owner plays Hawk while the intruder plays Dove. In this sense, the evolution of strategies in Hawk–Dove can be seen as the evolution of a sort of prototypical version of ownership. Game-theoretically, however, there is nothing special about this solution. The opposite solution—where the owner plays dove and the intruder plays Hawk—is equally stable. In fact, this solution is present in a certain species of spider; when an invader appears the occupying spider leaves. In order to explain the prevalence of property rights over "anti-property rights" one must discover a way to break this additional symmetry.
Replicator dynamics

Replicator dynamics In mathematics, the replicator equation is a deterministic monotone non-linear and non-innovative game dynamic used in evolutionary game theory. The replicator equation differs from other equations used to model replication, such as the quasispeci ...
is a simple model of strategy change commonly used in evolutionary game theory
Evolutionary game theory (EGT) is the application of game theory to evolving populations in biology. It defines a framework of contests, strategies, and analytics into which Darwinian competition can be modelled. It originated in 1973 with John Ma ...
. In this model, a strategy which does better than the average increases in frequency at the expense of strategies that do worse than the average. There are two versions of the replicator dynamics. In one version, there is a single population which plays against itself. In another, there are two population models where each population only plays against the other population (and not against itself).
In the one population model, the only stable state is the mixed strategy Nash equilibrium. Every initial population proportion (except all ''Hawk'' and all ''Dove'') converge to the mixed strategy Nash Equilibrium where part of the population plays ''Hawk'' and part of the population plays ''Dove''. (This occurs because the only ESS is the mixed strategy equilibrium.) In the two population model, this mixed point becomes unstable. In fact, the only stable states in the two population model correspond to the pure strategy equilibria, where one population is composed of all ''Hawks'' and the other of all ''Dove''s. In this model one population becomes the aggressive population while the other becomes passive. This model is illustrated by the vector field pictured in Figure 7a. The one-dimensional vector field of the single population model (Figure 7b) corresponds to the bottom left to top right diagonal of the two population model.
 The single population model presents a situation where no uncorrelated asymmetries exist, and so the best players can do is randomize their strategies. The two population models provide such an asymmetry and the members of each population will then use that to correlate their strategies. In the two population model, one population gains at the expense of another. Hawk–Dove and Chicken thus illustrate an interesting case where the qualitative results for the two different versions of the replicator dynamics differ wildly.
The single population model presents a situation where no uncorrelated asymmetries exist, and so the best players can do is randomize their strategies. The two population models provide such an asymmetry and the members of each population will then use that to correlate their strategies. In the two population model, one population gains at the expense of another. Hawk–Dove and Chicken thus illustrate an interesting case where the qualitative results for the two different versions of the replicator dynamics differ wildly.
Related strategies and games
Brinkmanship
"Chicken" and "Brinkmanship
Brinkmanship (or brinksmanship) is the practice of trying to achieve an advantageous outcome by pushing dangerous events to the brink of active conflict. The maneuver of pushing a situation with the opponent to the brink succeeds by forcing the op ...
" are often used synonymously in the context of conflict, but in the strict game-theoretic sense, "brinkmanship" refers to a strategic move A strategic move in game theory is an action taken by a player outside the defined actions of the game in order to gain a strategic advantage and increase one's payoff. Strategic moves can either be ''unconditional moves'' or ''response rules''. The ...
designed to avert the possibility of the opponent switching to aggressive behavior. The move involves a credible threat of the risk of irrational behavior in the face of aggression. If player 1 unilaterally moves to A, a rational player 2 cannot retaliate since (A, C) is preferable to (A, A). Only if player 1 has grounds to believe that there is sufficient risk that player 2 responds irrationally (usually by giving up control over the response, so that there is sufficient risk that player 2 responds with A) player 1 will retract and agree on the compromise.
War of attrition
Like "Chicken", the "War of attrition" game models escalation of conflict, but they differ in the form in which the conflict can escalate. Chicken models a situation in which the catastrophic outcome differs in kind from the agreeable outcome, e.g., if the conflict is over life and death. War of attrition models a situation in which the outcomes differ only in degrees, such as a boxing match in which the contestants have to decide whether the ultimate prize of victory is worth the ongoing cost of deteriorating health and stamina.Hawk–dove and war of attrition
The Hawk–Dove game is the most commonly used game theoretical model of aggressive interactions in biology. Thewar of attrition
The War of Attrition ( ar, حرب الاستنزاف, Ḥarb al-Istinzāf; he, מלחמת ההתשה, Milhemet haHatashah) involved fighting between Israel and Egypt, Jordan, the Palestine Liberation Organisation (PLO) and their allies from ...
is another very influential model of aggression in biology. The two models investigate slightly different questions. The Hawk–Dove game is a model of escalation, and addresses the question of when ought an individual escalate to dangerously costly physical combat. The war of attrition seeks to answer the question of how contests may be resolved when there is no possibility of physical combat. The war of attrition is an auction
An auction is usually a process of buying and selling goods or services by offering them up for bids, taking bids, and then selling the item to the highest bidder or buying the item from the lowest bidder. Some exceptions to this definition e ...
in which both players pay the lower bid (an all-pay second price auction). The bids are assumed to be the duration which the player is willing to persist in making a costly threat display
Deimatic behaviour or startle display means any pattern of bluffing behaviour in an animal that lacks strong defences, such as suddenly displaying conspicuous eyespots, to scare off or momentarily distract a predator, thus giving the prey anima ...
. Both players accrue costs while displaying at each other, the contest ends when the individual making the lower bid quits. Both players will then have paid the lower bid.
Chicken and prisoner's dilemma
Chicken is a symmetrical 2x2 game with conflicting interests, the preferred outcome is to play ''Straight'' while the opponent plays ''Swerve''. Similarly, theprisoner's dilemma
The Prisoner's Dilemma is an example of a game analyzed in game theory. It is also a thought experiment that challenges two completely rational agents to a dilemma: cooperate with their partner for mutual reward, or betray their partner ("de ...
is a symmetrical 2x2 game with conflicting interests: the preferred outcome is to ''Defect'' while the opponent plays ''Cooperate''. PD is about the impossibility of cooperation while Chicken is about the inevitability of conflict. Iterated play can solve PD but not Chicken.
Both games have a desirable cooperative outcome in which both players choose the less escalated strategy, ''Swerve-Swerve'' in the Chicken game, and ''Cooperate-Cooperate'' in the prisoner's dilemma, such that players receive the ''Coordination'' payoff C (see tables below). The temptation away from this sensible outcome is toward a ''Straight'' move in Chicken and a ''Defect'' move in the prisoner's dilemma (generating the Temptation payoff, should the other player use the less escalated move). The essential difference between these two games is that in the prisoner's dilemma, the ''Cooperate'' strategy is dominated, whereas in Chicken the equivalent move is not dominated since the outcome payoffs when the opponent plays the more escalated move (''Straight'' in place of ''Defect'') are reversed.
Schedule chicken and project management
The term "schedule chicken
Schedule chicken is a concept described in project management and software development circles. The condition occurs when two or more parties working towards a common goal all claim to be holding to their original schedules for delivering their p ...
" is used in project management
Project management is the process of leading the work of a team to achieve all project goals within the given constraints. This information is usually described in project documentation, created at the beginning of the development process. T ...
and software development
Software development is the process of conceiving, specifying, designing, programming, documenting, testing, and bug fixing involved in creating and maintaining applications, frameworks, or other software components. Software development inv ...
circles. The condition occurs when two or more areas of a product team claim they can deliver features at an unrealistically early date because each assumes the other teams are stretching the predictions even more than they are. This pretense continually moves forward past one project checkpoint to the next until feature integration
Integration may refer to:
Biology
* Multisensory integration
* Path integration
* Pre-integration complex, viral genetic material used to insert a viral genome into a host genome
*DNA integration, by means of site-specific recombinase technolo ...
begins or just before the functionality is actually due.
The practice of "schedule chicken" often results in contagious schedule slips due to the inter-team dependencies and is difficult to identify and resolve, as it is in the best interest of each team not to be the first bearer of bad news. The psychological drivers underlining the "schedule chicken" behavior in many ways mimic the hawk–dove or snowdrift model of conflict.
See also
*Brinkmanship
Brinkmanship (or brinksmanship) is the practice of trying to achieve an advantageous outcome by pushing dangerous events to the brink of active conflict. The maneuver of pushing a situation with the opponent to the brink succeeds by forcing the op ...
*Coordination game A coordination game is a type of simultaneous game found in game theory. It describes the situation where a player will earn a higher payoff when they select the same course of action as another player. The game is not one of pure conflict, which r ...
*Fireship
A fire ship or fireship, used in the days of wooden rowed or sailing ships, was a ship filled with combustibles, or gunpowder deliberately set on fire and steered (or, when possible, allowed to drift) into an enemy fleet, in order to destroy sh ...
, a naval tactic of intentional suicidal ramming into an enemy ship
*Matching pennies
Matching pennies is the name for a simple game used in game theory. It is played between two players, Even and Odd. Each player has a penny and must secretly turn the penny to heads or tails. The players then reveal their choices simultaneousl ...
*Mexican standoff
A Mexican standoff is a confrontation in which no strategy exists that allows any party to achieve victory. Any party initiating aggression might trigger its own demise. At the same time, the parties are unable to extricate themselves from the sit ...
*Prisoner's dilemma
The Prisoner's Dilemma is an example of a game analyzed in game theory. It is also a thought experiment that challenges two completely rational agents to a dilemma: cooperate with their partner for mutual reward, or betray their partner ("de ...
*Si vis pacem, para bellum
() is a Latin adage translated as "If you want peace, prepare for war".
The phrase ' is adapted from a statement found in Latin author Publius Flavius Vegetius Renatus's tract '' Dē Rē Mīlitārī'' (fourth or fifth century AD), in which ...
*Volunteer's dilemma
The volunteer's dilemma game models a situation in which each player can either make a small sacrifice that benefits everybody, or instead wait in hope of benefiting from someone else's sacrifice.
One example is a scenario in which the electricit ...
*War of attrition
The War of Attrition ( ar, حرب الاستنزاف, Ḥarb al-Istinzāf; he, מלחמת ההתשה, Milhemet haHatashah) involved fighting between Israel and Egypt, Jordan, the Palestine Liberation Organisation (PLO) and their allies from ...
*Zugzwang
Zugzwang (German for "compulsion to move", ) is a situation found in chess and other turn-based games wherein one player is put at a disadvantage because of their obligation to make a move; a player is said to be "in zugzwang" when any legal mov ...
Notes
References
* * * * * * * * * * * * * * * * *External links
The game of Chicken as a metaphor for human conflict
Game of Chicken – Rebel Without a Cause
by Elmer G. Wiens.
Online model: Expected Dynamics of an Imitation Model in the Hawk-Dove Game
Online model: Expected Dynamics of an Intra-Population Imitation Model in the Two-Population Hawk-Dove Game
{{Game theory Non-cooperative games Evolutionary game theory Endurance games Social science experiments