sinuosity on:
[Wikipedia]
[Google]
[Amazon]

 Sinuosity, sinuosity index, or sinuosity coefficient of a
Sinuosity, sinuosity index, or sinuosity coefficient of a
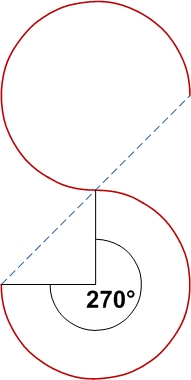 With similar opposite arcs joints in the same plane, continuously differentiable:
With similar opposite arcs joints in the same plane, continuously differentiable:

 Sinuosity, sinuosity index, or sinuosity coefficient of a
Sinuosity, sinuosity index, or sinuosity coefficient of a continuously differentiable
In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non- vertical tangent line at each interior point in ...
curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight.
Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ...
having at least one inflection point
In differential calculus and differential geometry, an inflection point, point of inflection, flex, or inflection (British English: inflexion) is a point on a smooth plane curve at which the curvature changes sign. In particular, in the case ...
is the ratio
In mathematics, a ratio shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ...
of the curvilinear length
In geometry, curvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally inve ...
(along the curve) and the Euclidean distance
In mathematics, the Euclidean distance between two points in Euclidean space is the length of a line segment between the two points.
It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, therefore o ...
(straight line
In geometry, a line is an infinitely long object with no width, depth, or curvature. Thus, lines are one-dimensional objects, though they may exist in two, three, or higher dimension spaces. The word ''line'' may also refer to a line segment ...
) between the end points of the curve. This dimensionless quantity
A dimensionless quantity (also known as a bare quantity, pure quantity, or scalar quantity as well as quantity of dimension one) is a quantity to which no physical dimension is assigned, with a corresponding SI unit of measurement of one (or 1) ...
can also be rephrased as the "actual path length" divided by the "shortest path length" of a curve.
The value ranges from 1 (case of straight line) to infinity (case of a closed loop, where the shortest path length is zero or for an infinitely-long actual path).
Interpretation
The curve must be continuous (no jump) between the two ends. The sinuosity value is really significant when the line is continuously differentiable (no angular point). The distance between both ends can also be evaluated by a plurality of segments according to a broken line passing through the successive inflection points (sinuosity of order 2). The calculation of the sinuosity is valid in a 3-dimensional space (e.g. for the central axis of thesmall intestine
The small intestine or small bowel is an organ in the gastrointestinal tract where most of the absorption of nutrients from food takes place. It lies between the stomach and large intestine, and receives bile and pancreatic juice through t ...
), although it is often performed in a plane (with then a possible orthogonal projection
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself (an endomorphism) such that P\circ P=P. That is, whenever P is applied twice to any vector, it gives the same result as if i ...
of the curve in the selected plan; "classic" sinuosity on the horizontal plane, longitudinal profile sinuosity on the vertical plane).
The classification of a sinuosity (e.g. strong / weak) often depends on the cartographic scale
The scale of a map is the ratio of a distance on the map to the corresponding distance on the ground. This simple concept is complicated by the curvature of the Earth's surface, which forces scale to vary across a map. Because of this variation, ...
of the curve (see the coastline paradox
The coastline paradox is the counterintuitive observation that the coastline of a landmass does not have a well-defined length. This results from the fractal curve-like properties of coastlines; i.e., the fact that a coastline typically has a ...
for further details) and of the object velocity which flowing therethrough (river, avalanche, car, bicycle, bobsleigh, skier, high speed train, etc.): the sinuosity of the same curved line could be considered very strong for a high speed train but low for a river. Nevertheless, it is possible to see a very strong sinuosity in the succession of few river bends, or of laces on some mountain roads.
Notable values
The sinuosity ''S'' of: * 2 inverted continuous semicircles located in the same plane is . It is independent of the circle radius; * asine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side that is opp ...
function (over a whole number ''n'' of half-periods), which can be calculated by computing the sine curve's arclength on those periods, is
 With similar opposite arcs joints in the same plane, continuously differentiable:
With similar opposite arcs joints in the same plane, continuously differentiable:
Rivers
In studies of rivers, the sinuosity index is similar but not identical to the general form given above, being given by: : The difference from the general form happens because the downvalley path is not perfectly straight. The sinuosity index can be explained, then, as the deviations from a path defined by the direction of maximum downslope. For this reason, bedrock streams that flow directly downslope have a sinuosity index of 1, andmeander
A meander is one of a series of regular sinuous curves in the channel of a river or other watercourse. It is produced as a watercourse erodes the sediments of an outer, concave bank ( cut bank) and deposits sediments on an inner, convex ban ...
ing streams have a sinuosity index that is greater than 1.
It is also possible to distinguish the case where the stream flowing on the line could not physically travel the distance between the ends: in some hydraulic studies, this leads to assign a sinuosity value of 1 for a torrent flowing over rocky bedrock along a horizontal rectilinear projection, even if the slope angle varies.
For rivers, the conventional classes of sinuosity, SI, are:
* SI <1.05: almost straight
* 1.05 ≤ SI <1.25: winding
* 1.25 ≤ SI <1.50: twisty
* 1.50 ≤ SI: meandering
It has been claimed that river shapes are governed by a self-organizing system
Self-organization, also called spontaneous order in the social sciences, is a process where some form of overall order arises from local interactions between parts of an initially disordered system. The process can be spontaneous when suffici ...
that causes their average sinuosity (measured in terms of the source-to-mouth distance, not channel length) to be , but this has not been borne out by later studies, which found an average value less than 2..
See also
*Curvature
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.
For curves, the can ...
* Oxbow lake
An oxbow lake is a U-shaped lake or pool that forms when a wide meander of a river is cut off, creating a free-standing body of water. In South Texas, oxbows left by the Rio Grande are called '' resacas''. In Australia, oxbow lakes are cal ...
References
{{River morphology Rivers Curves Ratios Curvature (mathematics)