Siamese method

The Siamese method, or De la Loubère method, is a simple method to construct any size of ''n''-odd magic squares (i.e. number squares in which the sums of all rows, columns and diagonals are identical). The method was brought to France in 1688 by the French mathematician and diplomat Simon de la Loubère, as he was returning from his 1687 embassy to the kingdom of Siam. The Siamese method makes the creation of magic squares straightforward.

Publication

De la Loubère published his findings in his book ''A new historical relation of the kingdom of Siam'' (''Du Royaume de Siam'', 1693), under the chapter entitled ''The problem of the magical square according to the Indians''.''A new historical relation of the kingdom of Siam'' p.228
/ref>
Although the method is generally qualified as "Siamese", which refers to de la Loubère's travel to the country of Siam, de la Loubère himself learnt it from a Frenchman named M.Vincent (a doctor, who had first travelled to Persia and then to Siam, and was returning to France with the de la Loubère embassy), who himself had learnt it in the city of Surat in India:

The method

The method was surprising in its effectiveness and simplicity:

First, an arithmetic progression has to be chosen (such as the simple progression 1,2,3,4,5,6,7,8,9 for a square with three rows and columns (the Lo Shu square)).

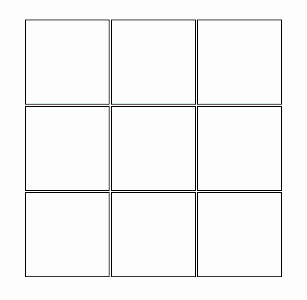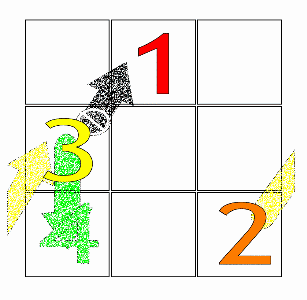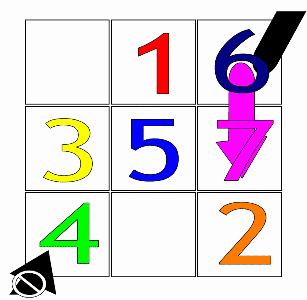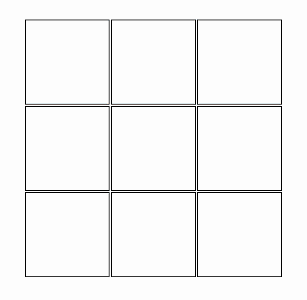
Then, starting from the central box of the first row with the number 1 (or the first number of any arithmetic progression), the fundamental movement for filling the boxes is diagonally up and right (↗), one step at a time. When a move would leave the square, it is wrapped around to the last row or first column, respectively.

If a filled box is encountered, one moves vertically down one box (↓) instead, then continuing as before.

Order-3 magic squares

Order-5 magic squares

Other sizes

Any ''n''-odd square (" odd-order square") can be thus built into a magic square. The Siamese method does not work however for n-even squares (" even-order squares", such as 2 rows/ 2 columns, 4 rows/ 4 columns etc...).

Other values

Any sequence of numbers can be used, provided they form an arithmetic progression (i.e. the difference of any two successive members of the sequence is a constant). Also, any starting number is possible. For example the following sequence can be used to form an order 3 magic square according to the Siamese method (9 boxes): 5, 10, 15, 20, 25, 30, 35, 40, 45 (the magic sum gives 75, for all rows, columns and diagonals). The magic sum in these cases will be the sum of the arithmetic progression used divided by the order of the magic square.

Other starting points

It is possible not to start the arithmetic progression from the middle of the top row, but then only the row and column sums will be identical and result in a magic sum, whereas the diagonal sums will differ. The result will thus not be a true magic square:

Rotations and reflections

Numerous other magic squares can be deduced from the above by simple rotations and reflections.

Variations

A slightly more complicated variation of this method exists in which the first number is placed in the box just above the center box. The fundamental movement for filling the boxes remains up and right (↗), one step at a time. However, if a filled box is encountered, one moves vertically up two boxes instead, then continuing as before.

Numerous variants can be obtained by simple rotations and reflections. The next square is equivalent to the above (a simple reflexion): the first number is placed in the box just below the center box. The fundamental movement for filling the boxes then becomes diagonally down and right (↘), one step at a time. If a filled box is encountered, one moves vertically down two boxes instead, then continuing as before.''A new historical relation of the kingdom of Siam'' p229
/ref>

These variations, although not quite as simple as the basic Siamese method, are equivalent to the methods developed by earlier Arab and European scholars, such as Manuel Moschopoulos (1315), Johann Faulhaber (1580–1635) and Claude Gaspard Bachet de Méziriac (1581–1638), and allowed to create magic squares similar to theirs.''The Zen of Magic Squares, Circles, and Stars'' by Clifford A. Pickover, 2002 p.3

/ref>

See also

* Conway's LUX method for magic squares
* Strachey method for magic squares

Notes and references

{{DEFAULTSORT:Siamese Method
Magic squares
Search algorithms