Shear flow

In solid mechanics, shear flow is the shear stress over a distance in a thin-walled structure.Higdon, Ohlsen, Stiles and Weese (1960), ''Mechanics of Materials'', article 4-9 (2nd edition), John Wiley & Sons, Inc., New York. Library of Congress CCN 66-25222 In fluid dynamics, shear flow is the flow ''induced'' by a force in a fluid.

In solid mechanics

For thin-walled profiles, such as that through a beam or semi-monocoque structure, the shear stress distribution through the thickness can be neglected. Furthermore, there is no shear stress in the direction normal to the wall, only parallel. In these instances, it can be useful to express internal shear stress as shear flow, which is found as the shear stress multiplied by the thickness of the section. An equivalent definition for shear flow is the shear force ''V'' per unit length of the perimeter around a thin-walled section. Shear flow has the dimensions of force per unit of length. This corresponds to units of newtons per meter in the SI system and pound-force per foot in the US.

Origin

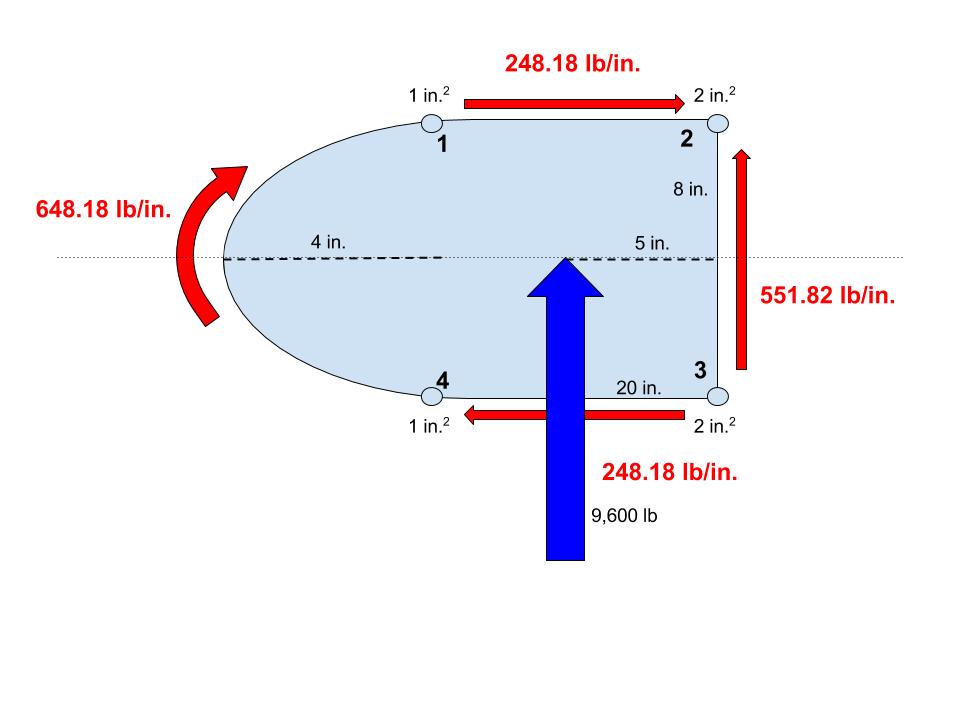
When a transverse force is applied to a beam, the result is variation in bending normal stresses along the length of the beam. This variation causes a horizontal shear stress within the beam that varies with distance from the neutral axis in the beam. The concept of complementary shear then dictates that a shear stress also exists across the cross section of the beam, in the direction of the original transverse force. As described above, in thin-walled structures, the variation along the thickness of the member can be neglected, so the shear stress across the cross section of a beam that is composed of thin-walled elements can be examined as shear flow, or the shear stress multiplied by the thickness of the element.

Applications

The concept of shear flow is particularly useful when analyzing semi-monocoque structures, which can be idealized using the skin-stringer model. In this model, the longitudinal members, or stringers, carry only axial stress, while the skin or web resists the externally applied torsion and shear force. In this case, since the skin is a thin-walled structure, the internal shear stresses in the skin can be represented as shear flow. In design, the shear flow is sometimes known before the skin thickness is determined, in which case the skin thickness can simply be sized according to allowable shear stress.

Shear center

For a given structure, the shear center is the point in space at which shear force could be applied without causing torsional deformation (e.g. twisting) of the cross-section of the structure. The shear center is an imaginary point, but does not vary with the magnitude of the shear force - only the cross-section of the structure. The shear center always lies along the axis of symmetry, and can be found using the following method:
# Apply an arbitrary resultant shear force
# Calculate the shear flows from this shear force
# Choose a reference point ''o'' an arbitrary distance ''e'' from the point of application of the load
# Calculate the moment about o using both shear flows and the resultant shear force, and equate the two expressions. Solve for ''e''
# The distance ''e'' and the axis of symmetry give the coordinate for the shear center, independent of the shear force magnitude.

Calculating shear flow

By definition, shear flow through a cross section of thickness t is calculated using $q = \tau t$, where $\tau = \frac$. Thus the equation for shear flow at a particular depth in a particular cross-section of a thin-walled structure that is symmetric across its width is
:$q = \frac$

where
: ''q'', the shear flow
: ''V''_''y'', the shear force perpendicular to the neutral axis ''x'' at the cross-section of interest
: ''Q''_''x'', the first moment of area (aka statical moment) about the neutral axis ''x'' for the cross section of the structure above the depth in question
: ''I''_''x'', the second moment of area (aka moment of inertia) about the neutral axis ''x'' for the structure (a function only of the shape of the structure)

In fluid mechanics

Unlike in solid mechanics where ''shear flow'' is the shear stress force per unit length, in fluid mechanics, ''shear flow'' (or ''shearing flow'') refers to adjacent layers of fluid moving parallel to each other with different speeds. Viscous fluids resist this shearing motion. For a Newtonian fluid, the stress exerted by the fluid in resistance to the shear is proportional to the strain rate or shear rate.

A simple example of a shear flow is Couette flow, in which a fluid is trapped between two large parallel plates, and one plate is moved with some relative velocity to the other. Here, the strain rate is simply the relative velocity divided by the distance between the plates.

Shear flows in fluids tend to be unstable at high Reynolds numbers, when fluid viscosity is not strong enough to dampen out perturbations to the flow. For example, when two layers of fluid shear against each other with relative velocity, the Kelvin–Helmholtz instability may occur.

Notes

References

*Riley, W. F. F., Sturges, L. D. and Morris, D. H. ''Mechanics of Materials.'' J. Wiley & Sons, New York, 1998 (5th Ed.), 720 pp. {{ISBN, 0-471-58644-7
*Weisshaar, T. A. ''Aerospace Structures: An Introduction to Fundamental Problems.'' T.A. Weisshaar, West Lafayette, 2009, 140pp.
*''Aerospace Mechanics and Materials.'' TU Delft OpenCourseWare. 11/22/16.

External links

Horizontal shearing stress

Shear flow

Solid mechanics
Fluid dynamics