Series expansions

In mathematics, a series expansion is a technique that expresses a function as an infinite sum, or series, of simpler functions. It is a method for calculating a function that cannot be expressed by just elementary operators (addition, subtraction, multiplication and division).

The resulting so-called '' series'' often can be limited to a finite number of terms, thus yielding an approximation of the function. The fewer terms of the sequence are used, the simpler this approximation will be. Often, the resulting inaccuracy (i.e., the partial sum of the omitted terms) can be described by an equation involving Big O notation (see also asymptotic expansion). The series expansion on an open interval will also be an approximation for non- analytic functions.

Types of series expansions

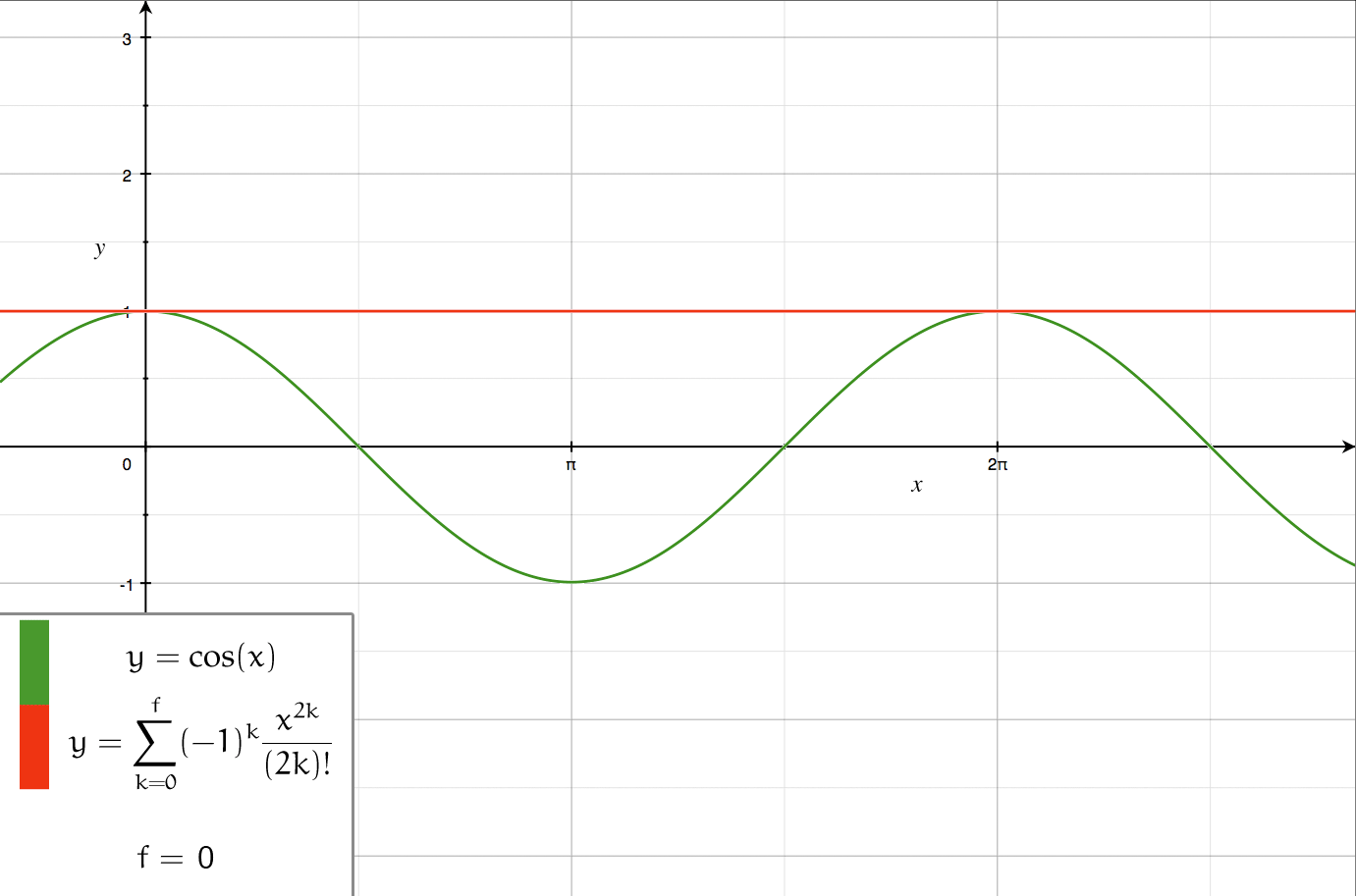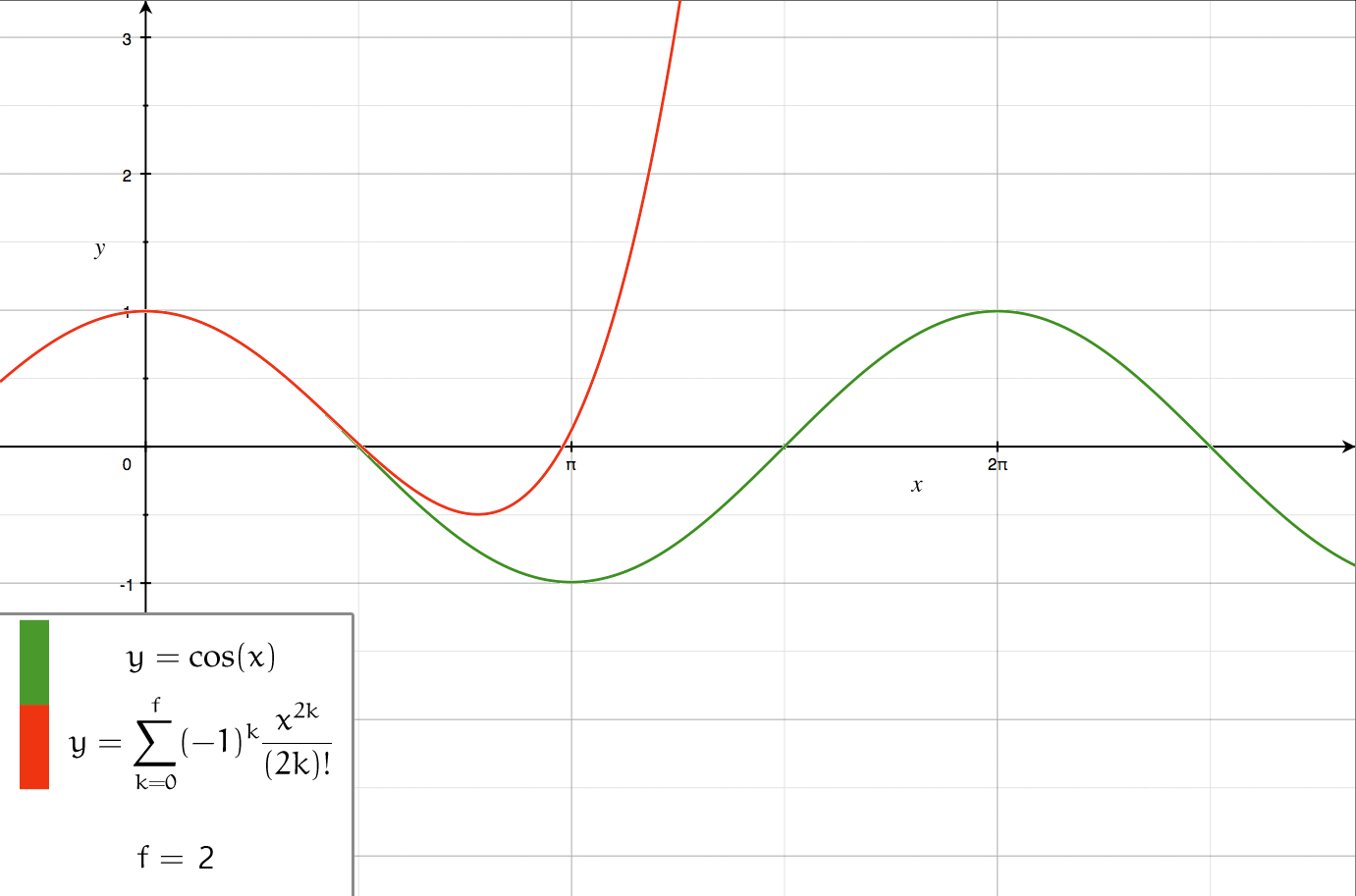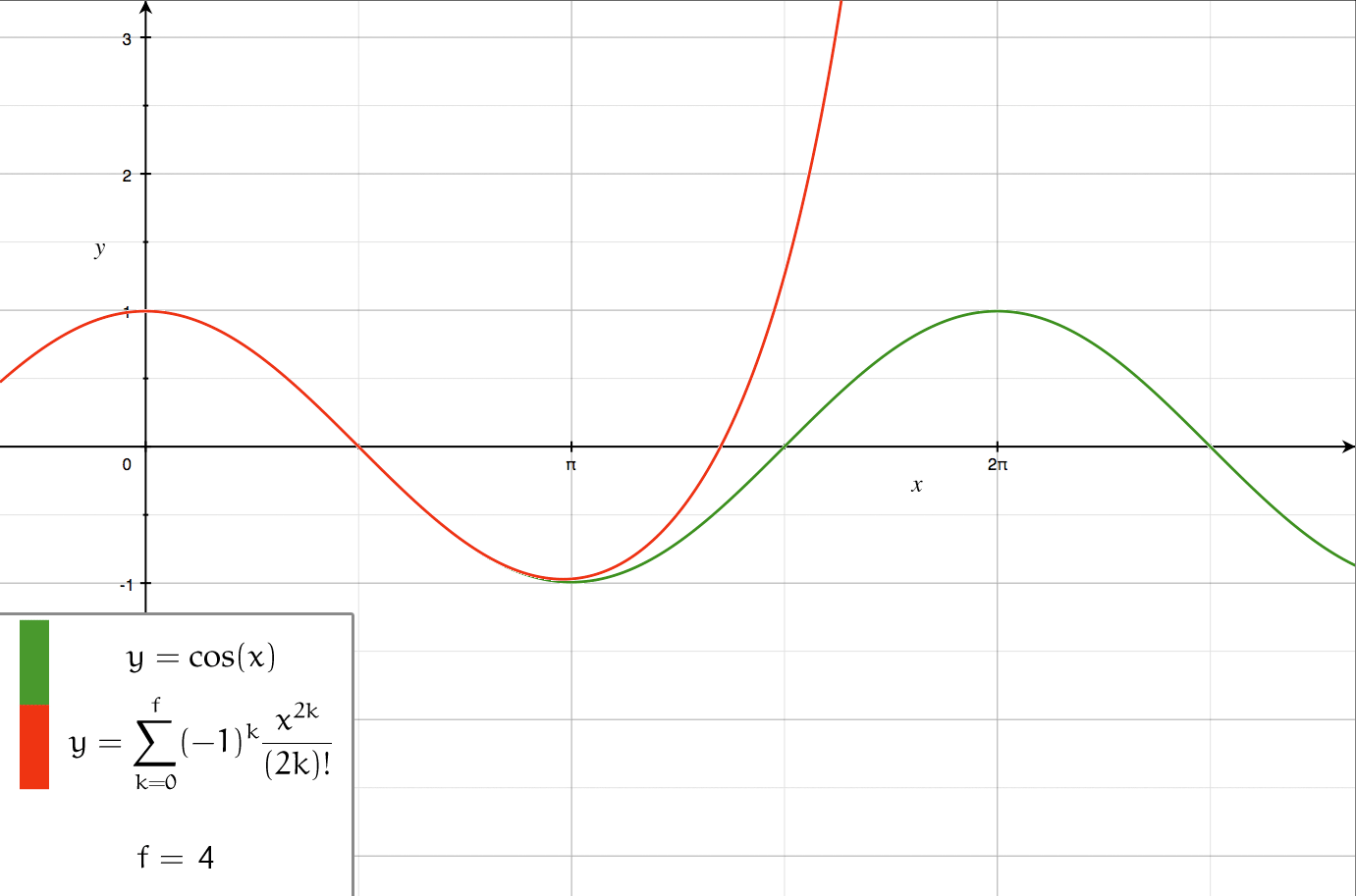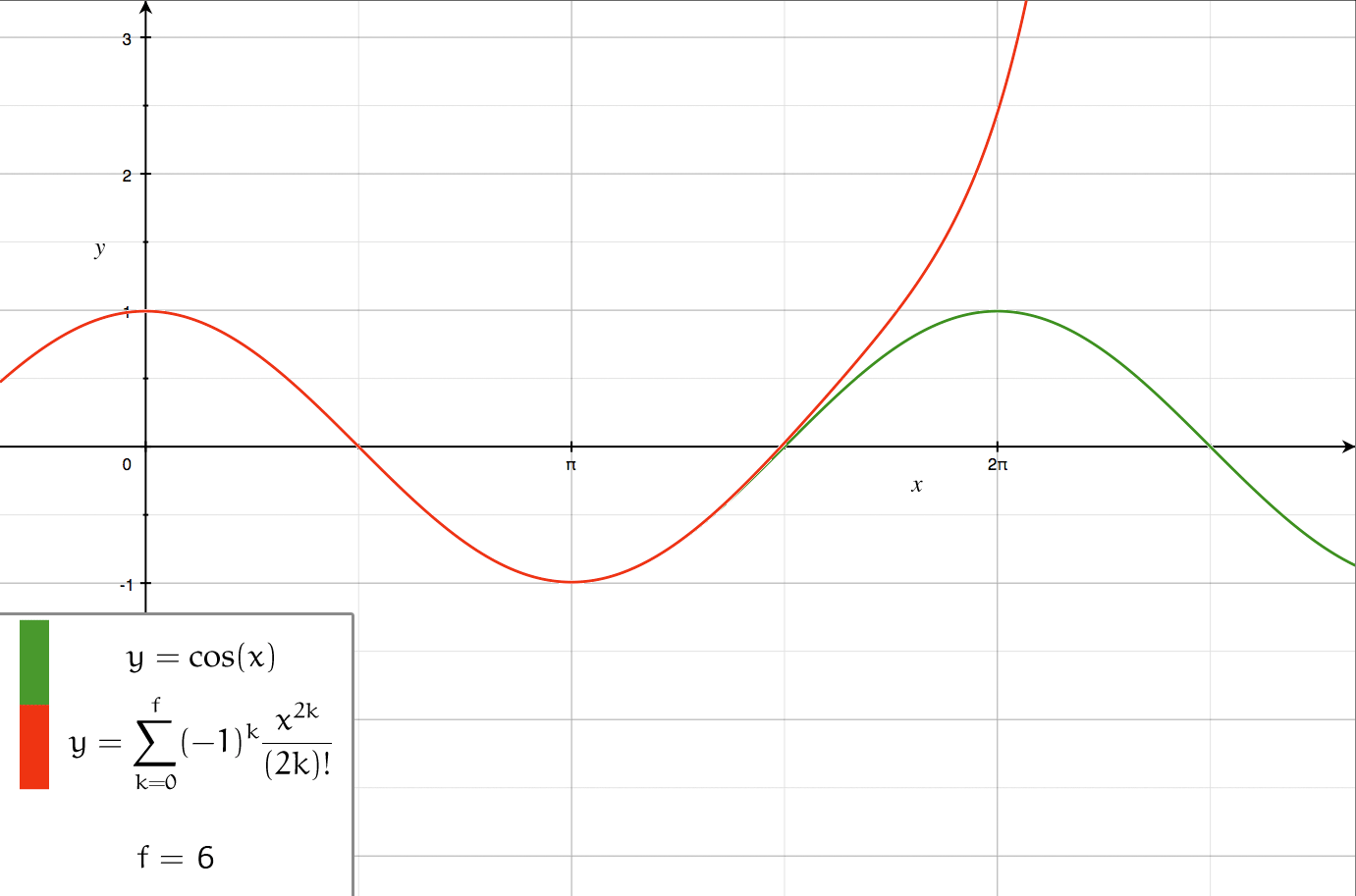
There are several kinds of series expansions, listed below.

Taylor series

A ''Taylor series'' is a power series based on a function's derivatives at a single point. More specifically, if a function $f: U\to\R$ is infinitely differentiable around a point $x_0$, then the Taylor series of ''f'' around this point is given by

$\sum_^\frac(x - x_0)^n$

under the convention $0^0 := 1$. The '' Maclaurin series'' of ''f'' is its Taylor series about $x_0 = 0$.

Laurent series

A ''Laurent series'' is a generalization of the Taylor series, allowing terms with negative exponents; it takes the form $\sum_^ c_k (z - a)^k$ and converges in an annulus. In particular, a Laurent series can be used to examine the behavior of a complex function near a singularity by considering the series expansion on an annulus centered at the singularity.

Dirichlet series

A ''general Dirichlet series'' is a series of the form $\sum_^ a_ne^.$ One important special case of this is the ''ordinary Dirichlet series'' $\sum_^\frac.$ Used in number theory.

Fourier series

A ''Fourier series'' is an expansion of periodic functions as a sum of many sine and cosine functions. More specifically, the Fourier series of a function $f(x)$ of period $2L$ is given by the expressiona_0 + \sum_^ \left _n\cos\left(\frac\right) + b_n\sin\left(\frac\right)\right/math>where the coefficients are given by the formulae$\begin a_n &:= \frac\int_^L f(x)\cos\left(\frac\right)dx, \\ b_n &:= \frac\int_^L f(x)\sin\left(\frac\right)dx. \end$

Other series

*In acoustics, e.g., the fundamental tone and the overtones together form an example of a Fourier series.

* Newtonian series

*Legendre polynomials: Used in physics to describe an arbitrary electrical field as a superposition of a dipole field, a quadrupole field, an octupole field, etc.

* Zernike polynomials: Used in optics to calculate aberrations of optical systems. Each term in the series describes a particular type of aberration.

*The '' Stirling series''$\text\Gamma\left(z\right)\sim\left(z-\tfrac\right)\ln z-z+\tfrac\ln\left(2\pi\right)+\sum_^\frac$is an approximation of the log-gamma function.

Examples

The following is the Taylor series of $e^x$:$e^x=\sum^_\frac= 1 + x + \frac + \frac...$

The Dirichlet series of the Riemann zeta function is$\zeta(s) := \sum_^ \frac = \frac + \frac{2^s} + \cdots$

References

Algebra
Polynomials
Mathematical analysis
Series (mathematics)