Samplesort

Samplesort is a sorting algorithm that is a divide and conquer algorithm often used in parallel processing systems. Conventional divide and conquer sorting algorithms partitions the array into sub-intervals or buckets. The buckets are then sorted individually and then concatenated together. However, if the array is non-uniformly distributed, the performance of these sorting algorithms can be significantly throttled. Samplesort addresses this issue by selecting a sample of size from the -element sequence, and determining the range of the buckets by sorting the sample and choosing elements from the result. These elements (called splitters) then divide the array into approximately equal-sized buckets. Samplesort is described in the 1970 paper, "Samplesort: A Sampling Approach to Minimal Storage Tree Sorting", by W. D. Frazer and A. C. McKellar.

Algorithm

Samplesort is a generalization of quicksort. Where quicksort partitions its input into two parts at each step, based on a single value called the pivot, samplesort instead takes a larger sample from its input and divides its data into buckets accordingly. Like quicksort, it then recursively sorts the buckets.

To devise a samplesort implementation, one needs to decide on the number of buckets . When this is done, the actual algorithm operates in three phases:
# Sample elements from the input (the ''splitters''). Sort these; each pair of adjacent splitters then defines a ''bucket''.
# Loop over the data, placing each element in the appropriate bucket. (This may mean: send it to a processor, in a multiprocessor system.)
# Sort each of the buckets.

The full sorted output is the concatenation of the buckets.

A common strategy is to set equal to the number of processors available. The data is then distributed among the processors, which perform the sorting of buckets using some other, sequential, sorting algorithm.

Pseudocode

The following listing shows the above mentioned three step algorithm as pseudocode and shows how the algorithm works in principle. In the following, is the unsorted data, is the oversampling factor, discussed later, and is the number of splitters.

function sampleSort(A ..n , )
// if average bucket size is below a threshold switch to e.g. quicksort
if ''n'' / ''k'' < threshold then smallSort(A)
/* Step 1 */
select ''S'' = 'S''₁, ..., ''S''_{(''p''−1)''k''}randomly from // select samples
sort // sort sample
's''₀, ''s''₁, ..., s_''p''−1, ''s''_''p''<- ∞, ''S''_''k'', ''S''_2''k'', ..., ''S''_{(''p''−1)''k''}, ∞// select splitters
/* Step 2 */
for each ''a'' in ''A''
find such that ''s''_''j''−1 < ''a'' <= ''s''_''j''
place in bucket ''b''_''j''
/* Step 3 and concatenation */
return concatenate(sampleSort(''b''₁), ..., sampleSort(''b''_''k''))

The pseudo code is different from the original Frazer and McKellar algorithm. In the pseudo code, samplesort is called recursively. Frazer and McKellar called samplesort just once and used quicksort in all following iterations.

Complexity

The complexity, given in Big O notation, for a parallelized implementation with $p$ processors:

Find the splitters.
:$O\left(\frac + \log(p)\right)$

Send to buckets.
:$O(p)$ for reading all nodes
:$O(\log(p))$ for broadcasting
:$O\left(\frac \log(p)\right)$ for binary search for all keys
:$O\left(\frac\right)$ to send keys to bucket

Sort buckets.
:$O\left(c\left(\frac\right) \right)$ where $c(n)$ is the complexity of the underlying sequential sorting method. Often $c(n) = n \log(n)$.

The number of comparisons, performed by this algorithm, approaches the information theoretical optimum $\log_2(n!)$ for big input sequences. In experiments, conducted by Frazer and McKellar, the algorithm needed 15% fewer comparisons than quicksort.

Sampling the data

The data may be sampled through different methods. Some methods include:
# Pick evenly spaced samples.
# Pick randomly selected samples.

Oversampling

The oversampling ratio determines how many times more data elements to pull as samples, before determining the splitters. The goal is to get a good representation of the distribution of the data. If the data values are widely distributed, in that there are not many duplicate values, then a small sampling ratio is sufficient. In other cases where there are many duplicates in the distribution, a larger oversampling ratio will be necessary. In the ideal case, after step 2, each bucket contains $n/p$ elements. In this case, no bucket takes longer to sort than the others, because all buckets are of equal size.

After pulling $k$ times more samples than necessary, the samples are sorted. Thereafter, the splitters used as bucket boundaries are the samples at position $k, 2k, 3k, \dots, (p-1)k$ of the sample sequence (together with $-\infty$ and $\infty$ as left and right boundaries for the left most and right most buckets respectively). This provides a better heuristic for good splitters than just selecting $p$ splitters randomly.

Bucket size estimate

With the resulting sample size, the expected bucket size and especially the probability of a bucket exceeding a certain size can be estimated. The following will show that for an oversampling factor of $S \in \Theta\left(\dfrac\right)$ the probability that no bucket has more than $(1 + \epsilon) \cdot \dfrac$ elements is larger than $1 - \dfrac$.

To show this let $\langle e_1, \dots, e_n\rangle$ be the input as a sorted sequence. For a processor to get more than $(1 + \epsilon) \cdot n/p$ elements, there has to exist a subsequence of the input of length $(1 + \epsilon) \cdot n/p$, of which a maximum of samples are picked. These cases constitute the probability $P_\text$. This can be represented as the random variable:
$X_i := \begin 1, & \text s_i \in \left\langle e_j, \dots, e_j + (1 + \epsilon) \cdot \dfrac\right\rangle\\ 0, & \text \end, X := \sum_^X_i$

For the expected value of $X_i$ holds:
$E(X_i) = P(X_i = 1) = \dfrac$

This will be used to estimate $P_\text$:
$P(X < S) \approx P(X < (1 - \epsilon^2)S) = P(X < (1 - \epsilon)E(X))$

Using the Chernoff bound now, it can be shown:
$P_\text = n \cdot P(X < S) \le n \cdot \exp\left(\dfrac\right) \le n \cdot \dfrac \text S \ge \dfrac\ln n$

Many identical keys

In case of many identical keys, the algorithm goes through many recursion levels where sequences are sorted, because the whole sequence consists of identical keys. This can be counteracted by introducing equality buckets. Elements equal to a pivot are sorted into their respective equality bucket, which can be implemented with only one additional conditional branch. Equality buckets are not further sorted. This works, since keys occurring more than $n/k$ times are likely to become pivots.

Uses in parallel systems

Samplesort is often used in parallel systems, including distributed systems such as bulk synchronous parallel machines. Due to the variable amount of splitters (in contrast to only one pivot in Quicksort), Samplesort is very well suited and intuitive for parallelization and scaling. Furthermore Samplesort is also more cache-efficient than implementations of e.g. quicksort.

Parallelization is implemented by splitting the sorting for each processor or node, where the number of buckets is equal to the number of processors $p$. Samplesort is efficient in parallel systems because each processor receives approximately the same bucket size $n/p$. Since the buckets are sorted concurrently, the processors will complete the sorting at approximately the same time, thus not having a processor wait for others.

On distributed systems, the splitters are chosen by taking $k$ elements on each processor, sorting the resulting $kp$ elements with a distributed sorting algorithm, taking every $k$-th element and broadcasting the result to all processors. This costs $T_\text(kp,p)$ for sorting the $kp$ elements on $p$ processors, as well as $T_\text(p,p)$ for distributing the $p$ chosen splitters to $p$ processors.

With the resulting splitters, each processor places its own input data into local buckets. This takes $\mathcal O(n/p\log p)$ with binary search. Thereafter, the local buckets are redistributed to the processors. Processor $i$ gets the local buckets $b_i$ of all other processors and sorts these locally. The distribution takes $T_\text(N, p)$ time, where $N$ is the size of the biggest bucket. The local sorting takes $T_\text(N)$.

Experiments performed in the early 1990s on Connection Machine supercomputers showed samplesort to be particularly good at sorting large datasets on these machines, because its incurs little interprocessor communication overhead. On latter-day GPUs, the algorithm may be less effective than its alternatives.

Efficient Implementation of Samplesort

As described above, the samplesort algorithm splits the elements according to the selected splitters. An efficient implementation strategy is proposed in the paper "Super Scalar Sample Sort". The implementation proposed in the paper uses two arrays of size $n$ (the original array containing the input data and a temporary one) for an efficient implementation. Hence, this version of the implementation is not an in-place algorithm.

In each recursion step, the data gets copied to the other array in a partitioned fashion. If the data is in the temporary array in the last recursion step, then the data is copied back to the original array.

Determining buckets

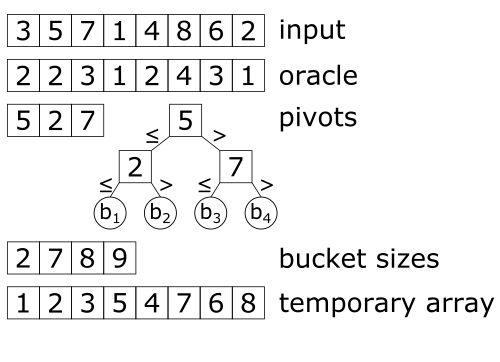
In a comparison based sorting algorithm the comparison operation is the most performance critical part. In Samplesort this corresponds to determining the bucket for each element. This needs $\log k$ time for each element.

Super Scalar Sample Sort uses a balanced search tree which is implicitly stored in an array . The root is stored at 0, the left successor of $t_i$ is stored at $t_$ and the right successor is stored at $t_$. Given the search tree , the algorithm calculates the bucket number of element $a_i$ as follows (assuming $a_i>t_j$ evaluates to 1 if it is ''true'' and 0 otherwise):

''j'' := 1
repeat log₂(''p'') times
''j'' := 2''j'' + (''a'' > ''t''_''j'')
''j'' := ''j'' − ''p'' + 1

Since the number of buckets is known at compile time, this loop can be unrolled by the compiler. The comparison operation is implemented with predicated instructions. Thus, there occur no branch mispredictions, which would slow down the comparison operation significantly.

Partitioning

For an efficient partitioning of the elements, the algorithm needs to know the sizes of the buckets in advance. To partition the elements of the sequence and put them into the array, we need to know the size of the buckets in advance. A naive algorithm could count the number of elements of each bucket. Then the elements could be inserted to the other array at the right place. Using this, one has to determine the bucket for each elements twice (one time for counting the number of elements in a bucket, and one time for inserting them).

To avoid this doubling of comparisons, Super Scalar Sample Sort uses an additional array $o$ (called oracle) which assigns each index of the elements to a bucket. First, the algorithm determines the contents of $o$ by determining the bucket for each element and the bucket sizes, and then placing the elements into the bucket determined by $o$. The array $o$ also incurs cost in storage space, but as it only needs to store $n\cdot \log k$ bits, these cost are small compared to the space of the input array.

In-place samplesort

A key disadvantage of the efficient Samplesort implementation shown above is that it is not in-place and requires a second temporary array of the same size as the input sequence during sorting. Efficient implementations of e.g. quicksort are in-place and thus more space efficient. However, Samplesort can be implemented in-place as well.

The in-place algorithm is separated into four phases:
# Sampling which is equivalent to the sampling in the above mentioned efficient implementation.
# Local Classification on each processor, which groups the input into blocks such that all elements in each block belong to the same bucket, but buckets are not necessarily continuous in memory.
# Block permutation brings the blocks into the globally correct order.
# Cleanup moves some elements on the edges of the buckets.

One obvious disadvantage of this algorithm is that it reads and writes every element twice, once in the classification phase and once in the block permutation phase. However, the algorithm performs up to three times faster than other state of the art in-place competitors and up to 1.5 times faster than other state of the art sequential competitors. As sampling was already discussed above, the three later stages will be further detailed in the following.

Local classification

In a first step, the input array is split up into $p$ stripes of blocks of equal size, one for each processor. Each processor additionally allocates $k$ buffers that are of equal size to the blocks, one for each bucket. Thereafter, each processor scans its stripe and moves the elements into the buffer of the according bucket. If a buffer is full, the buffer is written into the processors stripe, beginning at the front. There is always at least one buffer size of empty memory, because for a buffer to be written (i.e. buffer is full), at least a whole buffer size of elements more than elements written back had to be scanned. Thus, every full block contains elements of the same bucket. While scanning, the size of each bucket is kept track of.

Block permutation

Firstly, a prefix sum operation is performed that calculates the boundaries of the buckets. However, since only full blocks are moved in this phase, the boundaries are rounded up to a multiple of the block size and a single overflow buffer is allocated. Before starting the block permutation, some empty blocks might have to be moved to the end of its bucket. Thereafter, a write pointer $w_i$ is set to the start of the bucket $b_i$ subarray for each bucket and a read pointer $r_i$ is set to the last non empty block in the bucket $b_i$ subarray for each bucket.

To limit work contention, each processor is assigned a different primary bucket $b_$ and two swap buffers that can each hold a block. In each step, if both swap buffers are empty, the processor decrements the read pointer $r_$ of its primary bucket and reads the block at $r_$ and places it in one of its swap buffers. After determining the destination bucket $b_$ of the block by classifying the first element of the block, it increases the write pointer $w_$, reads the block at $w_$ into the other swap buffer and writes the block into its destination bucket. If $w_ > r_$, the swap buffers are empty again. Otherwise the block remaining in the swap buffers has to be inserted into its destination bucket.

If all blocks in the subarray of the primary bucket of a processor are in the correct bucket, the next bucket is chosen as the primary bucket. If a processor chose all buckets as primary bucket once, the processor is finished.

Cleanup

Since only whole blocks were moved in the block permutation phase, some elements might still be incorrectly placed around the bucket boundaries. Since there has to be enough space in the array for each element, those incorrectly placed elements can be moved to empty spaces from left to right, lastly considering the overflow buffer.

See also

* Flashsort
* Quicksort

References

External links

Frazer and McKellar's samplesort and derivatives:

Frazer and McKellar's original paper

DOI.org

DOI.org
Adapted for use on parallel computers:
* http://citeseer.ist.psu.edu/91922.html
* http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.49.214

{{sorting

Sorting algorithms
Distributed algorithms