rate–distortion theory

Rate–distortion theory is a major branch of information theory which provides the theoretical foundations for lossy data compression; it addresses the problem of determining the minimal number of bits per symbol, as measured by the rate ''R'', that should be communicated over a channel, so that the source (input signal) can be approximately reconstructed at the receiver (output signal) without exceeding an expected distortion ''D''.

Introduction

Rate–distortion theory gives an analytical expression for how much compression can be achieved using lossy compression methods. Many of the existing audio, speech, image, and video compression techniques have transforms, quantization, and bit-rate allocation procedures that capitalize on the general shape of rate–distortion functions.

Rate–distortion theory was created by Claude Shannon in his foundational work on information theory.

In rate–distortion theory, the ''rate'' is usually understood as the number of bits per data sample to be stored or transmitted. The notion of ''distortion'' is a subject of on-going discussion. In the most simple case (which is actually used in most cases), the distortion is defined as the expected value of the square of the difference between input and output signal (i.e., the mean squared error). However, since we know that most lossy compression techniques operate on data that will be perceived by human consumers (listening to music, watching pictures and video) the distortion measure should preferably be modeled on human perception and perhaps aesthetics: much like the use of probability in lossless compression, distortion measures can ultimately be identified with loss functions as used in Bayesian estimation and decision theory. In audio compression, perceptual models (and therefore perceptual distortion measures) are relatively well developed and routinely used in compression techniques such as MP3 or Vorbis, but are often not easy to include in rate–distortion theory. In image and video compression, the human perception models are less well developed and inclusion is mostly limited to the JPEG and MPEG weighting ( quantization, normalization) matrix.

Distortion functions

Distortion functions measure the cost of representing a symbol $x$ by an approximated symbol $\hat$. Typical distortion functions are the Hamming distortion and the Squared-error distortion.

Hamming distortion

:$d(x,\hat) = \begin 0 & \text x = \hat \\ 1 & \text x \neq \hat \end$

Squared-error distortion

:$d(x,\hat)=\left( x-\hat\right)^2$

Rate–distortion functions

The functions that relate the rate and distortion are found as the solution of the following minimization problem:

:$\inf_ I_Q(Y;X) \text D_Q \le D^*.$

Here $Q_(y\mid x)$, sometimes called a test channel, is the conditional probability density function (PDF) of the communication channel output (compressed signal) $Y$ for a given input (original signal) $X$, and $I_Q(Y;X)$ is the mutual information between $Y$ and $X$ defined as

:$I(Y;X) = H(Y) - H(Y\mid X) \,$

where $H(Y)$ and $H(Y\mid X)$ are the entropy of the output signal ''Y'' and the conditional entropy of the output signal given the input signal, respectively:

:$H(Y) = - \int_^\infty P_Y (y) \log_ (P_Y (y))\,dy$

:$H(Y\mid X) = - \int_^\infty \int_^\infty Q_(y\mid x) P_X (x) \log_2 (Q_ (y\mid x))\, dx\, dy.$

The problem can also be formulated as a distortion–rate function, where we find the infimum over achievable distortions for given rate constraint. The relevant expression is:

:\inf_ E _Q[X,Y \text I_Q(Y;X)\leq R.

The two formulations lead to functions which are inverses of each other.

The mutual information can be understood as a measure for 'prior' uncertainty the receiver has about the sender's signal (''H''(''Y'')), diminished by the uncertainty that is left after receiving information about the sender's signal ($H(Y\mid X)$). Of course the decrease in uncertainty is due to the communicated amount of information, which is $I \left(Y;X \right)$.

As an example, in case there is ''no'' communication at all, then $H(Y\mid X) = H (Y)$ and $I(Y;X) = 0$. Alternatively, if the communication channel is perfect and the received signal $Y$ is identical to the signal $X$ at the sender, then $H(Y\mid X) = 0$ and $I(Y;X) = H(X) = H(Y)$.

In the definition of the rate–distortion function, $D_Q$ and $D^$ are the distortion between $X$ and $Y$ for a given $Q_(y\mid x)$ and the prescribed maximum distortion, respectively. When we use the mean squared error as distortion measure, we have (for amplitude-continuous signals):

:$D_Q = \int_^\infty \int_^\infty P_(x,y) (x-y)^2\, dx\, dy = \int_^\infty \int_^\infty Q_(y\mid x)P_(x) (x-y)^2\, dx\, dy.$

As the above equations show, calculating a rate–distortion function requires the stochastic description of the input $X$ in terms of the PDF $P_X (x)$, and then aims at finding the conditional PDF $Q_(y\mid x)$ that minimize rate for a given distortion $D^$. These definitions can be formulated measure-theoretically to account for discrete and mixed random variables as well.

An analytical solution to this minimization problem is often difficult to obtain except in some instances for which we next offer two of the best known examples. The rate–distortion function of any source is known to obey several fundamental properties, the most important ones being that it is a continuous, monotonically decreasing convex (U) function and thus the shape for the function in the examples is typical (even measured rate–distortion functions in real life tend to have very similar forms).

Although analytical solutions to this problem are scarce, there are upper and lower bounds to these functions including the famous Shannon lower bound (SLB), which in the case of squared error and memoryless sources, states that for arbitrary sources with finite differential entropy,

:$R(D) \ge h(X) - h(D) \,$

where ''h''(''D'') is the differential entropy of a Gaussian random variable with variance D. This lower bound is extensible to sources with memory and other distortion measures. One important feature of the SLB is that it is asymptotically tight in the low distortion regime for a wide class of sources and in some occasions, it actually coincides with the rate–distortion function. Shannon Lower Bounds can generally be found if the distortion between any two numbers can be expressed as a function of the difference between the value of these two numbers.

The Blahut–Arimoto algorithm, co-invented by Richard Blahut, is an elegant iterative technique for numerically obtaining rate–distortion functions of arbitrary finite input/output alphabet sources and much work has been done to extend it to more general problem instances.

The computation of the rate-distortion function requires knowledge of the underlying distribution, which is often unavailable in contemporary applications in data-science and machine learning. However, this challenge can be addressed using deep learning-based estimators of the rate-distortion function. These estimators are typically referred to as 'neural estimators', involving the optimization of a parametrized variational form of the rate distortion objective.

When working with stationary sources with memory, it is necessary to modify the definition of the rate distortion function and it must be understood in the sense of a limit taken over sequences of increasing lengths.
:$R(D) = \lim_ R_n(D)$
where
:$R_n(D) = \frac \inf_ I(Y^n, X^n)$
and
:$\mathcal = \$
where superscripts denote a complete sequence up to that time and the subscript 0 indicates initial state.

Memoryless (independent) Gaussian source with squared-error distortion

If we assume that $X$ is a Gaussian random variable with variance $\sigma^2$, and if we assume that successive samples of the signal $X$ are stochastically independent (or equivalently, the source is ''memoryless'', or the signal is ''uncorrelated''), we find the following analytical expression for the rate–distortion function:

:$R(D) = \begin \frac\log_2(\sigma_x^2/D ), & \text 0 \le D \le \sigma_x^2 \\ 0, & \text D > \sigma_x^2. \end$   

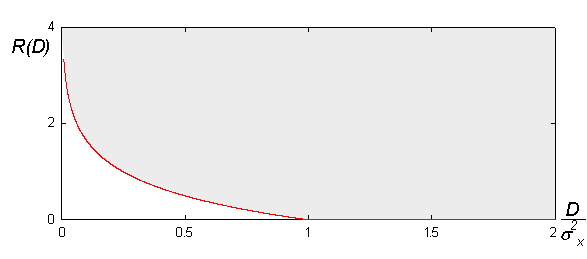
The following figure shows what this function looks like:

Rate–distortion theory tell us that 'no compression system exists that performs outside the gray area'. The closer a practical compression system is to the red (lower) bound, the better it performs. As a general rule, this bound can only be attained by increasing the coding block length parameter. Nevertheless, even at unit blocklengths one can often find good (scalar) quantizers that operate at distances from the rate–distortion function that are practically relevant.

This rate–distortion function holds only for Gaussian memoryless sources. It is known that the Gaussian source is the most "difficult" source to encode: for a given mean square error, it requires the greatest number of bits. The performance of a practical compression system working on—say—images, may well be below the $R \left(D \right)$ lower bound shown.

Memoryless (independent) Bernoulli source with Hamming distortion

The rate-distortion function of a Bernoulli random variable with Hamming distortion is given by:
:$R(D) = \left\{ \begin{matrix} H_b(p)-H_b(D), & 0 \le D \le \min{(p,1-p)} \\ 0, & D > \min{(p,1-p)} \end{matrix} \right.$
where $H_b$ denotes the binary entropy function.

Plot of the rate-distortion function for $p=0.5$:

Connecting rate-distortion theory to channel capacity

Suppose we want to transmit information about a source to the user with a distortion not exceeding ''D''. Rate–distortion theory tells us that at least $R(D)$ bits/symbol of information from the source must reach the user. We also know from Shannon's channel coding theorem that if the source entropy is ''H'' bits/symbol, and the channel capacity is ''C'' (where $C < H$), then $H-C$ bits/symbol will be lost when transmitting this information over the given channel. For the user to have any hope of reconstructing with a maximum distortion ''D'', we must impose the requirement that the information lost in transmission does not exceed the maximum tolerable loss of $H-R(D)$ bits/symbol. This means that the channel capacity must be at least as large as $R(D)$.

See also

*
*
*
*
*
*

References

External links

*
VcDemo Image and Video Compression Learning Tool

{{DEFAULTSORT:Rate-distortion theory
Data compression
Information theory