Quasiconvexity (Calculus Of Variations)

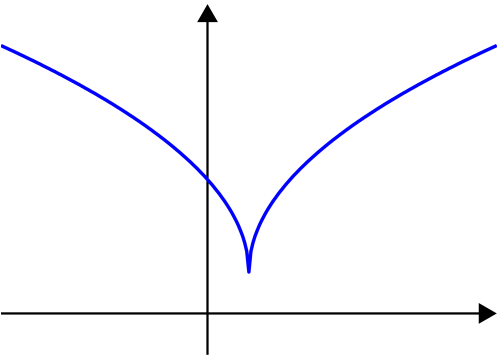
In mathematics, a quasiconvex function is a real-valued function defined on an interval or on a convex subset of a real vector space such that the inverse image of any set of the form $(-\infty,a)$ is a convex set. For a function of a single variable, along any stretch of the curve the highest point is one of the endpoints. The negative of a quasiconvex function is said to be quasiconcave.

All convex functions are also quasiconvex, but not all quasiconvex functions are convex, so quasiconvexity is a generalization of convexity. ''Univariate'' unimodal functions are quasiconvex or quasiconcave, however this is not necessarily the case for functions with multiple arguments. For example, the 2-dimensional Rosenbrock function is unimodal but not quasiconvex and functions with star-convex sublevel sets can be unimodal without being quasiconvex.

Definition and properties

A function $f:S \to \mathbb$ defined on a convex subset $S$ of a real vector space is quasiconvex if for all $x, y \in S$ and \lambda \in ,1/math> we have

: $f(\lambda x + (1 - \lambda)y)\leq\max\big\.$

In words, if $f$ is such that it is always true that a point directly between two other points does not give a higher value of the function than both of the other points do, then $f$ is quasiconvex. Note that the points $x$ and $y$, and the point directly between them, can be points on a line or more generally points in ''n''-dimensional space.

An alternative way (see introduction) of defining a quasi-convex function $f(x)$ is to require that each sublevel set
$S_\alpha(f) = \$
is a convex set.

If furthermore

: $f(\lambda x + (1 - \lambda)y)<\max\big\$

for all $x \neq y$ and $\lambda \in (0,1)$, then $f$ is strictly quasiconvex. That is, strict quasiconvexity requires that a point directly between two other points must give a lower value of the function than one of the other points does.

A quasiconcave function is a function whose negative is quasiconvex, and a strictly quasiconcave function is a function whose negative is strictly quasiconvex. Equivalently a function $f$ is quasiconcave if

: $f(\lambda x + (1 - \lambda)y)\geq\min\big\.$

and strictly quasiconcave if

: $f(\lambda x + (1 - \lambda)y)>\min\big\$

A (strictly) quasiconvex function has (strictly) convex lower contour sets, while a (strictly) quasiconcave function has (strictly) convex upper contour sets.

A function that is both quasiconvex and quasiconcave is quasilinear.

A particular case of quasi-concavity, if $S \subset \mathbb$, is unimodality, in which there is a locally maximal value.

Applications

Quasiconvex functions have applications in mathematical analysis, in mathematical optimization, and in game theory and economics.

Mathematical optimization

In nonlinear optimization, quasiconvex programming studies iterative methods that converge to a minimum (if one exists) for quasiconvex functions. Quasiconvex programming is a generalization of convex programming. Quasiconvex programming is used in the solution of "surrogate" dual problems, whose biduals provide quasiconvex closures of the primal problem, which therefore provide tighter bounds than do the convex closures provided by Lagrangian dual problems. In theory, quasiconvex programming and convex programming problems can be solved in reasonable amount of time, where the number of iterations grows like a polynomial in the dimension of the problem (and in the reciprocal of the approximation error tolerated); however, such theoretically "efficient" methods use "divergent-series" stepsize rules, which were first developed for classical subgradient methods. Classical subgradient methods using divergent-series rules are much slower than modern methods of convex minimization, such as subgradient projection methods, bundle methods of descent, and nonsmooth filter methods.

Economics and partial differential equations: Minimax theorems

In microeconomics, quasiconcave utility functions imply that consumers have convex preferences. Quasiconvex functions are important
also in game theory, industrial organization, and general equilibrium theory, particularly for applications of Sion's minimax theorem. Generalizing a minimax theorem of John von Neumann, Sion's theorem is also used in the theory of partial differential equations.

Preservation of quasiconvexity

Operations preserving quasiconvexity

* maximum of quasiconvex functions (i.e. $f = \max \left\lbrace f_1 , \ldots , f_n \right\rbrace$ ) is quasiconvex. Similarly, maximum of strict quasiconvex functions is strict quasiconvex. Similarly, the ''minimum'' of ''quasiconcave'' functions is quasiconcave, and the minimum of strictly-quasiconcave functions is strictly-quasiconcave.
* composition with a non-decreasing function : $g : \mathbb^ \rightarrow \mathbb$ quasiconvex, $h : \mathbb \rightarrow \mathbb$ non-decreasing, then $f = h \circ g$ is quasiconvex. Similarly, if $g : \mathbb^ \rightarrow \mathbb$ quasiconcave, $h : \mathbb \rightarrow \mathbb$ non-decreasing, then $f = h \circ g$ is quasiconcave.
* minimization (i.e. $f(x,y)$ quasiconvex, $C$ convex set, then $h(x) = \inf_ f(x,y)$ is quasiconvex)

Operations not preserving quasiconvexity

* The sum of quasiconvex functions defined on ''the same domain'' need not be quasiconvex: In other words, if $f(x), g(x)$ are quasiconvex, then $(f+g)(x) = f(x) + g(x)$ need not be quasiconvex.
* The sum of quasiconvex functions defined on ''different'' domains (i.e. if $f(x), g(y)$ are quasiconvex, $h(x,y) = f(x) + g(y)$) need not be quasiconvex. Such functions are called "additively decomposed" in economics and "separable" in mathematical optimization.

Examples

* Every convex function is quasiconvex.
* A concave function can be quasiconvex. For example, $x \mapsto \log(x)$ is both concave and quasiconvex.
* Any monotonic function is both quasiconvex and quasiconcave. More generally, a function which decreases up to a point and increases from that point on is quasiconvex (compare unimodality).
*The floor function $x\mapsto \lfloor x\rfloor$ is an example of a quasiconvex function that is neither convex nor continuous.

See also

* Convex function
* Concave function
* Logarithmically concave function
* Pseudoconvexity in the sense of several complex variables (not generalized convexity)
* Pseudoconvex function
* Invex function
* Concavification

References

* Avriel, M., Diewert, W.E., Schaible, S. and Zang, I., ''Generalized Concavity'', Plenum Press, 1988.
*
* Singer, Ivan ''Abstract convex analysis''. Canadian Mathematical Society Series of Monographs and Advanced Texts. A Wiley-Interscience Publication. John Wiley & Sons, Inc., New York, 1997. xxii+491 pp. 

External links

SION, M., "On general minimax theorems", Pacific J. Math. 8 (1958), 171-176.

Mathematical programming glossary

Concave and Quasi-Concave Functions
- by Charles Wilson, NYU Department of Economics

Quasiconcavity and quasiconvexity
- by Martin J. Osborne, University of Toronto Department of Economics

{{Convex analysis and variational analysis

Convex analysis
Convex optimization
Generalized convexity
Real analysis
Types of functions