Quantum Process Tomography on:
[Wikipedia]
[Google]
[Amazon]
Quantum 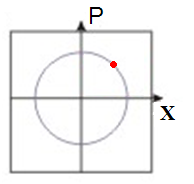 In quantum process tomography on the other hand, known
In quantum process tomography on the other hand, known 
tomography
Tomography is imaging by sections or sectioning that uses any kind of penetrating wave. The method is used in radiology, archaeology, biology, atmospheric science, geophysics, oceanography, plasma physics, materials science, astrophysics, quantu ...
or quantum state tomography is the process by which a quantum state is reconstructed using measurements on an ensemble of identical quantum states. The source of these states may be any device or system which prepares quantum states either consistently into quantum pure states
In quantum physics, a quantum state is a mathematical entity that provides a probability distribution for the outcomes of each possible measurement on a system. Knowledge of the quantum state together with the rules for the system's evolution i ...
or otherwise into general mixed states. To be able to uniquely identify the state, the measurements must be tomographically complete. That is, the measured operators
Operator may refer to:
Mathematics
* A symbol indicating a mathematical operation
* Logical operator or logical connective in mathematical logic
* Operator (mathematics), mapping that acts on elements of a space to produce elements of another sp ...
must form an operator basis
Basis may refer to:
Finance and accounting
*Adjusted basis, the net cost of an asset after adjusting for various tax-related items
*Basis point, 0.01%, often used in the context of interest rates
*Basis trading, a trading strategy consisting of ...
on the Hilbert space
In mathematics, Hilbert spaces (named after David Hilbert) allow generalizing the methods of linear algebra and calculus from (finite-dimensional) Euclidean vector spaces to spaces that may be infinite-dimensional. Hilbert spaces arise natural ...
of the system, providing all the information about the state. Such a set of observations is sometimes called a quorum. quantum states
In quantum physics, a quantum state is a mathematical entity that provides a probability distribution for the outcomes of each possible measurement in quantum mechanics, measurement on a system. Knowledge of the quantum state together with the rul ...
are used to probe a quantum process to find out how the process can be described. Similarly, quantum measurement tomography works to find out what measurement is being performed. Whereas, randomized benchmarking scalably obtains a figure of merit of the overlap between the error prone physical quantum process and its ideal counterpart.
The general principle behind quantum state tomography is that by repeatedly performing many different measurements on quantum systems described by identical density matrices, frequency counts can be used to infer probabilities
Probability is the branch of mathematics concerning numerical descriptions of how likely an event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and 1, where, roughly speaking, ...
, and these probabilities are combined with Born's rule
The Born rule (also called Born's rule) is a key postulate of quantum mechanics which gives the probability that a measurement of a quantum system will yield a given result. In its simplest form, it states that the probability density of findin ...
to determine a density matrix
In quantum mechanics, a density matrix (or density operator) is a matrix that describes the quantum state of a physical system. It allows for the calculation of the probabilities of the outcomes of any measurement performed upon this system, using ...
which fits the best with the observations.
This can be easily understood by making a classical analogy. Consider a harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its Mechanical equilibrium, equilibrium position, experiences a restoring force ''F'' Proportionality (mathematics), proportional to the displacement ''x'':
\v ...
(e.g. a pendulum). The position
Position often refers to:
* Position (geometry), the spatial location (rather than orientation) of an entity
* Position, a job or occupation
Position may also refer to:
Games and recreation
* Position (poker), location relative to the dealer
* ...
and momentum
In Newtonian mechanics, momentum (more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. If is an object's mass an ...
of the oscillator at any given point can be measured and therefore the motion can be completely described by the phase space
In dynamical system theory, a phase space is a space in which all possible states of a system are represented, with each possible state corresponding to one unique point in the phase space. For mechanical systems, the phase space usually ...
. This is shown in figure 1. By performing this measurement for a large number of identical oscillators we get a probability distribution in the phase space
In dynamical system theory, a phase space is a space in which all possible states of a system are represented, with each possible state corresponding to one unique point in the phase space. For mechanical systems, the phase space usually ...
(figure 2). This distribution can be normalized (the oscillator at a given time has to be somewhere) and the distribution must be non-negative. So we have retrieved a function W(x,p) which gives a description of the chance of finding the particle at a given point with a given momentum.
For quantum mechanical particles the same can be done. The only difference is that the Heisenberg's uncertainty principle
In quantum mechanics, the uncertainty principle (also known as Heisenberg's uncertainty principle) is any of a variety of mathematical inequalities asserting a fundamental limit to the accuracy with which the values for certain pairs of physic ...
mustn't be violated, meaning that we cannot measure the particle's momentum and position at the same time. The particle's momentum and its position are called quadratures (see Optical phase space
In quantum optics, an optical phase space is a phase space in which all quantum states of an optical system are described. Each point in the optical phase space corresponds to a unique state of an ''optical system''. For any such system, a plot of ...
for more information) in quantum related states. By measuring one of the quadratures of a large number of identical quantum states will give us a probability density corresponding to that particular quadrature. This is called the marginal distribution
In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. It gives the probabilities of various values of the variables ...
, pr(X) or pr(P) (see figure 3). In the following text we will see that this probability density is needed to characterize the particle's quantum state, which is the whole point of quantum tomography. What quantum state tomography is used for
Quantum tomography is applied on a source of systems, to determine thequantum state
In quantum physics, a quantum state is a mathematical entity that provides a probability distribution for the outcomes of each possible measurement on a system. Knowledge of the quantum state together with the rules for the system's evolution in ...
of the output of that source. Unlike a measurement on a single system, which determines the system's current state after the measurement (in general, the act of making a measurement alters the quantum state), quantum tomography works to determine the state(s) prior to the measurements.
Quantum tomography can be used for characterizing optical signals, including measuring the signal gain and loss of optical devices, as well as in quantum computing
Quantum computing is a type of computation whose operations can harness the phenomena of quantum mechanics, such as superposition, interference, and entanglement. Devices that perform quantum computations are known as quantum computers. Though ...
and quantum information theory
Quantum information is the information of the quantum state, state of a quantum system. It is the basic entity of study in quantum information theory, and can be manipulated using quantum information processing techniques. Quantum information re ...
to reliably determine the actual states of the qubits
In quantum computing, a qubit () or quantum bit is a basic unit of quantum information—the quantum version of the classic binary bit physically realized with a two-state device. A qubit is a two-state (or two-level) quantum-mechanical system, ...
. One can imagine a situation in which a person Bob prepares some quantum states
In quantum physics, a quantum state is a mathematical entity that provides a probability distribution for the outcomes of each possible measurement in quantum mechanics, measurement on a system. Knowledge of the quantum state together with the rul ...
and then gives the states to Alice to look at. Not confident with Bob's description of the states, Alice may wish to do quantum tomography to classify the states herself.
Methods of quantum state tomography
Linear inversion
UsingBorn's rule
The Born rule (also called Born's rule) is a key postulate of quantum mechanics which gives the probability that a measurement of a quantum system will yield a given result. In its simplest form, it states that the probability density of findin ...
, one can derive the simplest form of quantum tomography. Generally, being in a pure state is not known, and a state may be mixed. In this case, many different measurements will have to be performed, many times each. To fully reconstruct the density matrix
In quantum mechanics, a density matrix (or density operator) is a matrix that describes the quantum state of a physical system. It allows for the calculation of the probabilities of the outcomes of any measurement performed upon this system, using ...
for a mixed state in a finite-dimensional
In mathematics, the dimension of a vector space ''V'' is the cardinality (i.e., the number of vectors) of a basis of ''V'' over its base field. p. 44, §2.36 It is sometimes called Hamel dimension (after Georg Hamel) or algebraic dimension to disti ...
Hilbert space
In mathematics, Hilbert spaces (named after David Hilbert) allow generalizing the methods of linear algebra and calculus from (finite-dimensional) Euclidean vector spaces to spaces that may be infinite-dimensional. Hilbert spaces arise natural ...
, the following technique may be used.
Born's rule
The Born rule (also called Born's rule) is a key postulate of quantum mechanics which gives the probability that a measurement of a quantum system will yield a given result. In its simplest form, it states that the probability density of findin ...
states , where is a particular measurement outcome projector
A projector or image projector is an optical device that projects an image (or moving images) onto a surface, commonly a projection screen. Most projectors create an image by shining a light through a small transparent lens, but some newer types ...
and is the density matrix of the system.
Given a histogram
A histogram is an approximate representation of the distribution of numerical data. The term was first introduced by Karl Pearson. To construct a histogram, the first step is to " bin" (or "bucket") the range of values—that is, divide the ent ...
of observations for each measurement, one has an approximation
to for each .
Given linear operators
In mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a mapping V \to W between two vector spaces that pre ...
and , define the inner product
:
where is representation of the operator as a column vector and a row vector such that is the inner product in of the two.
Define the matrix as
:.
Here ''E''i is some fixed list of individual measurements (with binary outcomes), and ''A'' does all the measurements at once.
Then applying this to yields the probabilities
Probability is the branch of mathematics concerning numerical descriptions of how likely an event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and 1, where, roughly speaking, ...
:
:.
Linear inversion corresponds to inverting this system using the observed relative frequencies to derive (which is isomorphic to ).
This system is not going to be square in general, as for each measurement being made there will generally be multiple measurement outcome projector
A projector or image projector is an optical device that projects an image (or moving images) onto a surface, commonly a projection screen. Most projectors create an image by shining a light through a small transparent lens, but some newer types ...
s . For example, in a 2-D Hilbert space
In mathematics, Hilbert spaces (named after David Hilbert) allow generalizing the methods of linear algebra and calculus from (finite-dimensional) Euclidean vector spaces to spaces that may be infinite-dimensional. Hilbert spaces arise natural ...
with 3 measurements , each measurement has 2 outcomes, each of which has a projector ''E''i, for 6 projectors, whereas the real dimension of the space of density matrices is (2⋅22)/2=4, leaving to be 6 x 4. To solve the system, multiply on the left by :
:.
Now solving for yields the pseudoinverse
In mathematics, and in particular, algebra, a generalized inverse (or, g-inverse) of an element ''x'' is an element ''y'' that has some properties of an inverse element but not necessarily all of them. The purpose of constructing a generalized inv ...
:
:.
This works in general only if the measurement list ''E''i is tomographically complete. Otherwise, the matrix will not be invertible
In mathematics, the concept of an inverse element generalises the concepts of opposite () and reciprocal () of numbers.
Given an operation denoted here , and an identity element denoted , if , one says that is a left inverse of , and that is ...
.
Continuous variables and quantum homodyne tomography
In infinite dimensionalHilbert spaces
In mathematics, Hilbert spaces (named after David Hilbert) allow generalizing the methods of linear algebra and calculus from (finite-dimensional) Euclidean vector spaces to spaces that may be infinite-dimensional. Hilbert spaces arise naturally ...
, e.g. in measurements of continuous variables such as position, the methodology is somewhat more complex. One notable example is in the tomography
Tomography is imaging by sections or sectioning that uses any kind of penetrating wave. The method is used in radiology, archaeology, biology, atmospheric science, geophysics, oceanography, plasma physics, materials science, astrophysics, quantu ...
of light
Light or visible light is electromagnetic radiation that can be perceived by the human eye. Visible light is usually defined as having wavelengths in the range of 400–700 nanometres (nm), corresponding to frequencies of 750–420 tera ...
, known as optical homodyne
In electrical engineering, homodyne detection is a method of extracting information encoded as modulation of the phase and/or frequency of an oscillating signal, by comparing that signal with a standard oscillation that would be identical to the ...
tomography
Tomography is imaging by sections or sectioning that uses any kind of penetrating wave. The method is used in radiology, archaeology, biology, atmospheric science, geophysics, oceanography, plasma physics, materials science, astrophysics, quantu ...
. Using balanced homodyne
In electrical engineering, homodyne detection is a method of extracting information encoded as modulation of the phase and/or frequency of an oscillating signal, by comparing that signal with a standard oscillation that would be identical to the ...
measurements, one can derive the Wigner function and a density matrix
In quantum mechanics, a density matrix (or density operator) is a matrix that describes the quantum state of a physical system. It allows for the calculation of the probabilities of the outcomes of any measurement performed upon this system, using ...
for the state of the light
Light or visible light is electromagnetic radiation that can be perceived by the human eye. Visible light is usually defined as having wavelengths in the range of 400–700 nanometres (nm), corresponding to frequencies of 750–420 tera ...
.
One approach involves measurements along different rotated directions in phase space
In dynamical system theory, a phase space is a space in which all possible states of a system are represented, with each possible state corresponding to one unique point in the phase space. For mechanical systems, the phase space usually ...
. For each direction , one can find a probability distribution
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon i ...
for the probability density
In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can ...
of measurements in the direction of phase space yielding the value . Using an inverse Radon transformation
In mathematics, the Radon transform is the integral transform which takes a function ''f'' defined on the plane to a function ''Rf'' defined on the (two-dimensional) space of lines in the plane, whose value at a particular line is equal to the l ...
(the filtered back projection) on leads to the Wigner function, , which can be converted by an inverse Fourier transform In mathematics, the Fourier inversion theorem says that for many types of functions it is possible to recover a function from its Fourier transform. Intuitively it may be viewed as the statement that if we know all frequency and phase information ...
into the density matrix
In quantum mechanics, a density matrix (or density operator) is a matrix that describes the quantum state of a physical system. It allows for the calculation of the probabilities of the outcomes of any measurement performed upon this system, using ...
for the state in any basis. A similar technique is often used in medical tomography.
Example: single-qubit state tomography
The density matrix of a single qubit can be expressed in terms of itsBloch vector
In quantum mechanics and computing, the Bloch sphere is a geometrical representation of the pure state space of a two-level quantum mechanical system (qubit), named after the physicist Felix Bloch.
Quantum mechanics is mathematically formulate ...
and the Pauli vector
In mathematical physics and mathematics, the Pauli matrices are a set of three complex matrices which are Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma (), they are occasionally denoted by tau () when used in c ...
:
: .
The single-qubit state tomography can be performed by means of single-qubit Pauli measurements:
# First, create a list of three quantum circuits, with the first one measuring the qubit in the computational basis (''Z''-basis), the second one performing a Hadamard gate
The Hadamard transform (also known as the Walsh–Hadamard transform, Hadamard–Rademacher–Walsh transform, Walsh transform, or Walsh–Fourier transform) is an example of a generalized class of Fourier transforms. It performs an orthogonal ...
before measurement (which makes the measurement in ''X''-basis), and the third one performing the appropriate phase shift gate (that is ) followed by a Hadamard gate before measurement (which makes the measurement in ''Y''-basis);
# Then, run these circuits (typically thousands of times), and the counts in the measurement results of the first circuit produces , the second circuit , and the third circuit ;
# Finally, if , then a measured Bloch vector is produced as , and the measured density matrix is ; If , it'll be necessary to renormalize the measured Bloch vector as before using it to calculate the measured density matrix.
This algorithm is the foundation for qubit tomography and is used in some quantum programming
Quantum programming is the process of assembling sequences of instructions, called quantum circuits, that are capable of running on a quantum computer. Quantum programming languages help express quantum algorithms using high-level constructs. T ...
routines, like that of Qiskit
Qiskit is an open-source Software development kit, software development kit (SDK) for working with Quantum Computer, quantum computers at the level of circuits, pulses, and algorithms. It provides tools for creating and manipulating Quantum circu ...
.
Example: homodyne tomography.
Field amplitudes or quadratures with high efficiencies can be measured withphotodetectors
Photodetectors, also called photosensors, are sensors of light or other electromagnetic radiation. There is a wide variety of photodetectors which may be classified by mechanism of detection, such as photoelectric or photochemical effects, or by ...
together with temporal mode selectivity. Balanced homodyne tomography is a reliable technique of reconstructing quantum state
In quantum physics, a quantum state is a mathematical entity that provides a probability distribution for the outcomes of each possible measurement on a system. Knowledge of the quantum state together with the rules for the system's evolution in ...
s in the optical domain. This technique combines the advantages of the high efficiencies of photodiodes in measuring the intensity or photon number
In quantum mechanics, a Fock state or number state is a quantum state that is an element of a Fock space with a well-defined number of particles (or quanta). These states are named after the Soviet physicist Vladimir Fock. Fock states play an impo ...
of light, together with measuring the quantum features of light by a clever set-up called the homodyne tomography
Tomography is imaging by sections or sectioning that uses any kind of penetrating wave. The method is used in radiology, archaeology, biology, atmospheric science, geophysics, oceanography, plasma physics, materials science, astrophysics, quantu ...
detector. This is explained by the following example.
A laser
A laser is a device that emits light through a process of optical amplification based on the stimulated emission of electromagnetic radiation. The word "laser" is an acronym for "light amplification by stimulated emission of radiation". The fir ...
is directed onto a 50-50% beamsplitter
A beam splitter or ''beamsplitter'' is an optical device that splits a beam of light into a transmitted and a reflected beam. It is a crucial part of many optical experimental and measurement systems, such as interferometers, also finding wide ...
, splitting the laserbeam into two beams. One is used as local oscillator
In electronics, a local oscillator (LO) is an electronic oscillator used with a mixer to change the frequency of a signal. This frequency conversion process, also called heterodyning, produces the sum and difference frequencies from the frequenc ...
(LO) and the other is used to generate photons with a particular quantum state
In quantum physics, a quantum state is a mathematical entity that provides a probability distribution for the outcomes of each possible measurement on a system. Knowledge of the quantum state together with the rules for the system's evolution in ...
. The generation of quantum states can be realized, e.g. by directing the laser beam through a frequency doubling
Second-harmonic generation (SHG, also called frequency doubling) is a nonlinear optics, nonlinear optical process in which two photons with the same frequency interact with a nonlinear material, are "combined", and generate a new photon with tw ...
crystal
A crystal or crystalline solid is a solid material whose constituents (such as atoms, molecules, or ions) are arranged in a highly ordered microscopic structure, forming a crystal lattice that extends in all directions. In addition, macros ...
and then onto a parametric down-conversion
Spontaneous parametric down-conversion (also known as SPDC, parametric fluorescence or parametric scattering) is a nonlinear instant optical process that converts one photon of higher energy (namely, a pump photon), into a pair of photons (namely, ...
crystal. This crystal generates two photons in a certain quantum state. One of the photons is used as a trigger signal used to trigger (start) the readout event of the homodyne tomography detector. The other photon is directed into the homodyne tomography detector, in order to reconstruct its quantum state. Since the trigger and signal photons are entangled (this is explained by the Spontaneous parametric down-conversion
Spontaneous parametric down-conversion (also known as SPDC, parametric fluorescence or parametric scattering) is a nonlinear instant optical process that converts one photon of higher energy (namely, a pump photon), into a pair of photons (namely, ...
article), it is important to realize, that the optical mode of the signal state is created nonlocal only when the trigger photon impinges the photodetector (of the trigger event readout module) and is actually measured. More simply said, it is only when the trigger photon is measured, that the signal photon can be measured by the homodyne detector.
Now consider the homodyne
In electrical engineering, homodyne detection is a method of extracting information encoded as modulation of the phase and/or frequency of an oscillating signal, by comparing that signal with a standard oscillation that would be identical to the ...
tomography
Tomography is imaging by sections or sectioning that uses any kind of penetrating wave. The method is used in radiology, archaeology, biology, atmospheric science, geophysics, oceanography, plasma physics, materials science, astrophysics, quantu ...
detector as depicted in figure 4 (figure missing). The signal photon (this is the quantum state
In quantum physics, a quantum state is a mathematical entity that provides a probability distribution for the outcomes of each possible measurement on a system. Knowledge of the quantum state together with the rules for the system's evolution in ...
we want to reconstruct) interferes with the local oscillator
In electronics, a local oscillator (LO) is an electronic oscillator used with a mixer to change the frequency of a signal. This frequency conversion process, also called heterodyning, produces the sum and difference frequencies from the frequenc ...
, when they are directed onto a 50-50% beamsplitter
A beam splitter or ''beamsplitter'' is an optical device that splits a beam of light into a transmitted and a reflected beam. It is a crucial part of many optical experimental and measurement systems, such as interferometers, also finding wide ...
. Since the two beams originate from the same so called master laser
A laser is a device that emits light through a process of optical amplification based on the stimulated emission of electromagnetic radiation. The word "laser" is an acronym for "light amplification by stimulated emission of radiation". The fir ...
, they have the same fixed phase
Phase or phases may refer to:
Science
*State of matter, or phase, one of the distinct forms in which matter can exist
*Phase (matter), a region of space throughout which all physical properties are essentially uniform
* Phase space, a mathematic ...
relation. The local oscillator must be intense, compared to the signal so it provides a precise phase reference. The local oscillator is so intense, that we can treat it classically (a = α) and neglect the quantum fluctuations.
The signal field is spatially and temporally controlled by the local oscillator, which has a controlled shape. Where the local oscillator is zero, the signal is rejected. Therefore, we have temporal-spatial mode selectivity of the signal.
The beamsplitter redirects the two beams to two photodetectors. The photodetectors generate an electric current
An electric current is a stream of charged particles, such as electrons or ions, moving through an electrical conductor or space. It is measured as the net rate of flow of electric charge through a surface or into a control volume. The moving pa ...
proportional to the photon number
In quantum mechanics, a Fock state or number state is a quantum state that is an element of a Fock space with a well-defined number of particles (or quanta). These states are named after the Soviet physicist Vladimir Fock. Fock states play an impo ...
. The two detector currents are subtracted and the resulting current is proportional to the electric field operator
In physics, canonical quantization is a procedure for quantizing a classical theory, while attempting to preserve the formal structure, such as symmetries, of the classical theory, to the greatest extent possible.
Historically, this was not quite ...
in the signal mode, depended on relative optical phase of signal and local oscillator.
Since the electric field amplitude of the local oscillator is much higher than that of the signal the intensity or fluctuations in the signal field can be seen. The homodyne tomography system functions as an amplifier
An amplifier, electronic amplifier or (informally) amp is an electronic device that can increase the magnitude of a signal (a time-varying voltage or current). It may increase the power significantly, or its main effect may be to boost the v ...
. The system can be seen as an interferometer
Interferometry is a technique which uses the ''interference'' of superimposed waves to extract information. Interferometry typically uses electromagnetic waves and is an important investigative technique in the fields of astronomy, fiber op ...
with such a high intensity reference beam (the local oscillator) that unbalancing the interference by a single photon in the signal is measurable. This amplification is well above the photodetectors noise floor
In signal theory, the noise floor is the measure of the signal created from the sum of all the noise sources and unwanted signals within a measurement system, where noise is defined as any signal other than the one being monitored.
In radio com ...
.
The measurement is reproduced a large number of times. Then the phase difference between the signal and local oscillator is changed in order to ‘scan’ a different angle
In Euclidean geometry, an angle is the figure formed by two Ray (geometry), rays, called the ''Side (plane geometry), sides'' of the angle, sharing a common endpoint, called the ''vertex (geometry), vertex'' of the angle.
Angles formed by two ...
in the phase space
In dynamical system theory, a phase space is a space in which all possible states of a system are represented, with each possible state corresponding to one unique point in the phase space. For mechanical systems, the phase space usually ...
. This can be seen from figure 4. The measurement is repeated again a large number of times and a marginal distribution
In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. It gives the probabilities of various values of the variables ...
is retrieved from the current difference. The marginal distribution
In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. It gives the probabilities of various values of the variables ...
can be transformed into the density matrix
In quantum mechanics, a density matrix (or density operator) is a matrix that describes the quantum state of a physical system. It allows for the calculation of the probabilities of the outcomes of any measurement performed upon this system, using ...
and/or the Wigner function. Since the density matrix
In quantum mechanics, a density matrix (or density operator) is a matrix that describes the quantum state of a physical system. It allows for the calculation of the probabilities of the outcomes of any measurement performed upon this system, using ...
and the Wigner function give information about the quantum state
In quantum physics, a quantum state is a mathematical entity that provides a probability distribution for the outcomes of each possible measurement on a system. Knowledge of the quantum state together with the rules for the system's evolution in ...
of the photon, we have reconstructed the quantum state of the photon.
The advantage of this method is that this arrangement is insensitive to fluctuations in the frequency
Frequency is the number of occurrences of a repeating event per unit of time. It is also occasionally referred to as ''temporal frequency'' for clarity, and is distinct from ''angular frequency''. Frequency is measured in hertz (Hz) which is eq ...
of the laser
A laser is a device that emits light through a process of optical amplification based on the stimulated emission of electromagnetic radiation. The word "laser" is an acronym for "light amplification by stimulated emission of radiation". The fir ...
.
The quantum computations for retrieving the quadrature component from the current difference are performed as follows.
The photon number
In quantum mechanics, a Fock state or number state is a quantum state that is an element of a Fock space with a well-defined number of particles (or quanta). These states are named after the Soviet physicist Vladimir Fock. Fock states play an impo ...
operator for the beams striking the photodetectors after the beamsplitter is given by:
:,
where i is 1 and 2, for respectively beam one and two.
The mode operators of the field emerging the beamsplitters are given by:
:
:
The denotes the annihilation operator of the signal and alpha the complex amplitude of the local oscillator.
The number of photon difference is eventually proportional to the quadrature and given by:
:,
Rewriting this with the relation:
:
Results in the following relation:
:,
where we see clear relation between the photon number
In quantum mechanics, a Fock state or number state is a quantum state that is an element of a Fock space with a well-defined number of particles (or quanta). These states are named after the Soviet physicist Vladimir Fock. Fock states play an impo ...
difference and the quadrature component . By keeping track of the sum current, one can recover information about the local oscillator's intensity, since this is usually an unknown quantity, but an important quantity for calculating the quadrature component .
Problems with linear inversion
One of the primary problems with using linear inversion to solve for thedensity matrix
In quantum mechanics, a density matrix (or density operator) is a matrix that describes the quantum state of a physical system. It allows for the calculation of the probabilities of the outcomes of any measurement performed upon this system, using ...
is that in general the computed solution will not be a valid density matrix. For example, it could give negative probabilities
Probability is the branch of mathematics concerning numerical descriptions of how likely an event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and 1, where, roughly speaking, ...
or probabilities greater than 1 to certain measurement outcomes. This is particularly an issue when fewer measurements are made.
Another issue is that in infinite dimensional Hilbert spaces
In mathematics, Hilbert spaces (named after David Hilbert) allow generalizing the methods of linear algebra and calculus from (finite-dimensional) Euclidean vector spaces to spaces that may be infinite-dimensional. Hilbert spaces arise naturally ...
, an infinite number of measurement outcomes would be required. Making assumptions about the structure and using a finite measurement basis leads to artifacts in the phase space density.
Maximum likelihood estimation
Maximum likelihood estimation
In statistics, maximum likelihood estimation (MLE) is a method of estimating the parameters of an assumed probability distribution, given some observed data. This is achieved by maximizing a likelihood function so that, under the assumed statis ...
(also known as MLE or MaxLik) is a popular technique for dealing with the problems of linear inversion. By restricting the domain of density matrices
In quantum mechanics, a density matrix (or density operator) is a matrix that describes the quantum state of a physical system. It allows for the calculation of the probabilities of the outcomes of any Measurement in quantum mechanics, measurement ...
to the proper space, and searching for the density matrix which maximizes the likelihood
The likelihood function (often simply called the likelihood) represents the probability of random variable realizations conditional on particular values of the statistical parameters. Thus, when evaluated on a given sample, the likelihood funct ...
of giving the experimental results, it guarantees the state to be theoretically valid while giving a close fit to the data. The likelihood of a state is the probability that would be assigned to the observed results had the system been in that state.
Suppose the measurements have been observed with frequencies . Then the likelihood associated with a state is
:
where is the probability of outcome for the state .
Finding the maximum of this function is non-trivial and generally involves iterative methods. The methods are an active topic of research.
Problems with maximum likelihood estimation
Maximum likelihood estimation suffers from some less obvious problems than linear inversion. One problem is that it makes predictions about probabilities that cannot be justified by the data. This is seen most easily by looking at the problem of zeroeigenvalues
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted b ...
. The computed solution using MLE often contains eigenvalues
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted b ...
which are 0, i.e. it is rank deficient
In linear algebra, the rank of a matrix is the dimension of the vector space generated (or spanned) by its columns. p. 48, § 1.16 This corresponds to the maximal number of linearly independent columns of . This, in turn, is identical to the dime ...
. In these cases, the solution then lies on the boundary
Boundary or Boundaries may refer to:
* Border, in political geography
Entertainment
*Boundaries (2016 film), ''Boundaries'' (2016 film), a 2016 Canadian film
*Boundaries (2018 film), ''Boundaries'' (2018 film), a 2018 American-Canadian road trip ...
of the n-dimensional Bloch sphere
In quantum quantum mechanics, mechanics and Quantum computing, computing, the Bloch sphere is a geometrical representation of the pure state space of a two-level system, two-level quantum mechanical system (qubit), named after the physicist Felix ...
. This can be seen as related to linear inversion giving states which lie outside the valid space (the Bloch sphere). MLE in these cases picks a nearby point that is valid, and the nearest points are generally on the boundary.
This is not physically a problem, the real state might have zero eigenvalues
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted b ...
. However, since no value may be less than 0, an estimate of an eigenvalue being 0 implies that the estimator is certain the value is 0, otherwise they would have estimated some greater than 0 with a small degree of uncertainty
Uncertainty refers to epistemic situations involving imperfect or unknown information. It applies to predictions of future events, to physical measurements that are already made, or to the unknown. Uncertainty arises in partially observable or ...
as the best estimate. This is where the problem arises, in that it is not logical to conclude with absolute certainty after a finite number of measurements that any eigenvalue (that is, the probability of a particular outcome) is 0. For example, if a coin is flipped 5 times and each time heads was observed, it does not mean there is 0 probability of getting tails, despite that being the most ''likely'' description of the coin.
Bayesian methods
Bayesian
Thomas Bayes (/beɪz/; c. 1701 – 1761) was an English statistician, philosopher, and Presbyterian minister.
Bayesian () refers either to a range of concepts and approaches that relate to statistical methods based on Bayes' theorem, or a follower ...
mean estimation (BME) is a relatively new approach which addresses the problems of maximum likelihood estimation. It focuses on finding optimal solutions which are also ''honest'' in that they include error bars in the estimate. The general idea is to start with a likelihood function
The likelihood function (often simply called the likelihood) represents the probability of random variable realizations conditional on particular values of the statistical parameters. Thus, when evaluated on a given sample, the likelihood funct ...
and a function describing the experimenter's prior knowledge (which might be a constant function), then integrate over all density matrices using the product of the likelihood function
The likelihood function (often simply called the likelihood) represents the probability of random variable realizations conditional on particular values of the statistical parameters. Thus, when evaluated on a given sample, the likelihood funct ...
and prior knowledge function as a weight.
Given a reasonable prior knowledge function, BME will yield a state strictly within the n-dimensional Bloch sphere
In quantum quantum mechanics, mechanics and Quantum computing, computing, the Bloch sphere is a geometrical representation of the pure state space of a two-level system, two-level quantum mechanical system (qubit), named after the physicist Felix ...
. In the case of a coin flipped N times to get N heads described above, with a constant prior knowledge function, BME would assign as the probability for tails.
BME provides a high degree of accuracy in that it minimizes the ''operational divergences'' of the estimate from the actual state.
Methods for incomplete data
The number of measurements needed for a full quantum state tomography for a multi-particle system scales exponentially with the number of particles, which makes such a procedure impossible even for modest system sizes. Hence, several methods have been developed to realize quantum tomography with fewer measurements. The concept ofmatrix completion
Matrix completion is the task of filling in the missing entries of a partially observed matrix, which is equivalent to performing data imputation in statistics. A wide range of datasets are naturally organized in matrix form. One example is the mo ...
and compressed sensing
Compressed sensing (also known as compressive sensing, compressive sampling, or sparse sampling) is a signal processing technique for efficiently acquiring and reconstructing a Signal (electronics), signal, by finding solutions to Underdetermined ...
have been applied to reconstruct density matrices from an incomplete set of measurements (that is, a set of measurements which is not a quorum). In general, this is impossible, but under assumptions (for example, if the density matrix is a pure state, or a combination of just a few pure states) then the density matrix has fewer degrees of freedom, and it may be possible to reconstruct the state from the incomplete measurements.
Permutationally Invariant Quantum TomographyPermutationally Invariant Quantum Tomography.
is a procedure that has been developed mostly for states that are close to being
permutationally symmetric, which is typical in nowadays experiments. For two-state particles, the number of measurements needed scales only quadratically with the number of particles.
Besides the modest measurement effort, the processing of the measured data can also be done efficiently:
It is possible to carry out the fitting of a physical density matrix on the measured data even for large systems.
Permutationally Invariant Quantum Tomography has been combined with compressed sensing in a six-qubit
photonic experiment.
Quantum measurement tomography
One can imagine a situation in which an apparatus performs some measurement on quantum systems, and determining what particular measurement is desired. The strategy is to send in systems of various known states, and use these states to estimate the outcomes of the unknown measurement. Also known as "quantum estimation", tomography techniques are increasingly important including those for quantum measurement tomography and the very similar quantum state tomography. Since a measurement can always be characterized by a set ofPOVM
In functional analysis and quantum measurement theory, a positive operator-valued measure (POVM) is a measure whose values are positive semi-definite operators on a Hilbert space. POVMs are a generalisation of projection-valued measures (PVM) and ...
's, the goal is to reconstruct the characterizing POVM
In functional analysis and quantum measurement theory, a positive operator-valued measure (POVM) is a measure whose values are positive semi-definite operators on a Hilbert space. POVMs are a generalisation of projection-valued measures (PVM) and ...
's . The simplest approach is linear inversion. As in quantum state observation, use
:.
Exploiting linearity as above, this can be inverted to solve for the .
Not surprisingly, this suffers from the same pitfalls as in quantum state tomography: namely, non-physical results, in particular negative probabilities. Here the will not be valid POVM
In functional analysis and quantum measurement theory, a positive operator-valued measure (POVM) is a measure whose values are positive semi-definite operators on a Hilbert space. POVMs are a generalisation of projection-valued measures (PVM) and ...
's, as they will not be positive. Bayesian methods as well as Maximum likelihood estimation
In statistics, maximum likelihood estimation (MLE) is a method of estimating the parameters of an assumed probability distribution, given some observed data. This is achieved by maximizing a likelihood function so that, under the assumed statis ...
of the density matrix
In quantum mechanics, a density matrix (or density operator) is a matrix that describes the quantum state of a physical system. It allows for the calculation of the probabilities of the outcomes of any measurement performed upon this system, using ...
can be used to restrict the operators to valid physical results.
Quantum process tomography
Quantum process tomography (QPT) deals with identifying an unknown quantum dynamical process. The first approach, introduced in 1996 and sometimes known as standard quantum process tomography (SQPT) involves preparing an ensemble of quantum states and sending them through the process, then using quantum state tomography to identify the resultant states. Other techniques include ancilla-assisted process tomography (AAPT) and entanglement-assisted process tomography (EAPT) which require an extra copy of the system. Each of the techniques listed above are known as ''indirect methods'' for characterization of quantum dynamics, since they require the use of quantum state tomography to reconstruct the process. In contrast, there are ''direct methods'' such as direct characterization of quantum dynamics (DCQD) which provide a full characterization of quantum systems without any state tomography. The number of experimental configurations (state preparations and measurements) required for full quantum process tomography grows exponentially with the number of constituent particles of a system. Consequently, in general, QPT is an impossible task for large-scale quantum systems. However, under weak decoherence assumption, a quantum dynamical map can find a sparse representation. The method of compressed quantum process tomography (CQPT) uses thecompressed sensing
Compressed sensing (also known as compressive sensing, compressive sampling, or sparse sampling) is a signal processing technique for efficiently acquiring and reconstructing a Signal (electronics), signal, by finding solutions to Underdetermined ...
technique and applies the sparsity assumption to reconstruct a quantum dynamical map from an incomplete set of measurements or test state preparations.
Quantum dynamical maps
A quantum process, also known as a quantum dynamical map, , can be described by acompletely positive map
In mathematics a positive map is a map between C*-algebras that sends positive elements to positive elements. A completely positive map is one which satisfies a stronger, more robust condition.
Definition
Let A and B be C*-algebras. A linear m ...
:,
where , the bounded operators on Hilbert space
In mathematics, Hilbert spaces (named after David Hilbert) allow generalizing the methods of linear algebra and calculus from (finite-dimensional) Euclidean vector spaces to spaces that may be infinite-dimensional. Hilbert spaces arise natural ...
; with ''operation elements'' satisfying so that .
Let be an orthogonal basis for . Write the operators in this basis
:.
This leads to
:,
where .
The goal is then to solve for , which is a positive superoperator
In physics, a superoperator is a linear operator acting on a vector space of linear operators.John Preskill, Lecture notes for Quantum Computation course at CaltechCh. 3
Sometimes the term refers more specially to a completely positive map which ...
and completely characterizes with respect to the basis.
Standard quantum process tomography
SQPT approaches this usinglinearly independent
In the theory of vector spaces, a set of vectors is said to be if there is a nontrivial linear combination of the vectors that equals the zero vector. If no such linear combination exists, then the vectors are said to be . These concepts are ...
inputs , where is the dimension of the Hilbert space . For each of these input states , sending it through the process gives an output state which can be written as a linear combination of the , i.e. . By sending each through many times, quantum state tomography can be used to determine the coefficients experimentally.
Write
:,
where is a matrix of coefficients.
Then
:.
Since form a linearly independent basis,
:.
Inverting gives :
:.
References