Proportional Approval Voting on:
[Wikipedia]
[Google]
[Amazon]
Proportional approval voting (PAV) is a proportional
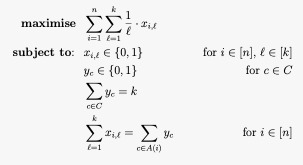 Computing the winning committee under PAV is
Computing the winning committee under PAV is
''abcvoting''
However, when ''k'' is fixed, the computation of the PAV winning subset is computable in polynomial time, i.e. , where ''n'' is the number of voters.
electoral system
An electoral system or voting system is a set of rules that determine how elections and Referendum, referendums are conducted and how their results are determined. Electoral systems are used in politics to elect governments, while non-political ...
for selecting committees. It is an extension of the D'Hondt method
The D'Hondt method, also called the Jefferson method or the greatest divisors method, is a method for allocating seats in parliaments among federal states, or in party-list proportional representation systems. It belongs to the class of highest- ...
of apportionment
The legal term apportionment (french: apportionement; Mediaeval Latin: , derived from la, portio, share), also called delimitation, is in general the distribution or allotment of proper shares, though may have different meanings in different c ...
that additionally allows for personal votes (voters vote for candidates, not for a party list). The voters vote via approval ballot An approval ballot, also called an unordered ballot, is a ballot in which a voter may vote for any number of candidates simultaneously, rather than for just one candidate. Candidates that are selected in a voter's ballot are said to be ''approved'' ...
s where each voter marks those candidates that the voter finds acceptable.
History
The system was first proposed byThorvald N. Thiele
Thorvald Nicolai Thiele (24 December 1838 – 26 September 1910) was a Danish astronomer and director of the Copenhagen Observatory. He was also an actuary and mathematician, most notable for his work in statistics, interpolation and the three- ...
. It was used in combination with ranked voting
The term ranked voting (also known as preferential voting or ranked choice voting) refers to any voting system in which voters ranking, rank their candidates (or options) in a sequence of first or second (or third, etc.) on their respective ball ...
in the early 20th century in Sweden, for example between 1909 and 1921 for distributing seats within parties, and in local elections. After 1921 it was replaced by Phragmén's rules. PAV was rediscovered by Forest Simmons in 2001 who gave it the name "proportional approval voting".
Definition
PAV selects a committee of a fixed desired size with the highest score, where scores are calculated according to the following formula. Given a committee , for each voter we check how many candidates in the committee the voter approves. Assuming that the voter voted for candidates in , the voter contributes to the score of the value of the -thharmonic number
In mathematics, the -th harmonic number is the sum of the reciprocals of the first natural numbers:
H_n= 1+\frac+\frac+\cdots+\frac =\sum_^n \frac.
Starting from , the sequence of harmonic numbers begins:
1, \frac, \frac, \frac, \frac, \dot ...
, that is:
:
The score of is calculated as the sum of the scores garnered from all the voters.
Formally, assume we have a set of candidates , a set of voters , and a committee size . Let denote the set of candidates approved by voter . The PAV score of a committee with size is defined as . PAV select the committee with the maximal score.
Example 1
Assume 2 seats to be filled, and the are four candidates: Andrea (A), Brad (B), Carter (C), and Delilah (D), and 30 voters. The ballots are: * 5 voters voted for A and B * 17 voters voted for A and C * 8 voters voted for D There are 6 possible results: AB, AC, AD, BC, BD, and CD. Andrea and Carter are elected. Note that Simple Approval shows that Andrea has 22 votes, Carter has 17 votes, Delilah has 8 votes and Brad has 5 votes. In this case, the PAV selection of Andrea and Carter is coincident with the Simple Approval sequence. However, if the above votes are changed slightly so that A and C receive 16 votes and D receives 9 votes, then Andrea and Delilah are elected since the A and C score is now 29 while the A and D score remains at 30. Also, the sequence created by using Simple Approval remains unchanged. This shows that PAV can give results that are incompatible with the method which simply follows the sequence implied by Simple Approval.Example 2
Assume there are 10 seats to be selected, and there are three groups of candidates: red, blue, and green candidates. There are 100 voters: * 60 voters voted for all blue candidates, * 30 voters voted for all red candidates, * 10 voters voted for all green candidates. In this case PAV would select 6 blue, 3 red, and 1 green candidate. The score of such a committee would beAll other committees receive a lower score. For example, the score of a committee that consists of only blue candidates would be : In this example, the outcome of PAV is proportional: the number of candidates selected from each group is proportional to the number of voters voting for the group. This is not coincidence: If the candidates form disjoint groups, as in the above example (the groups can be viewed as political parties), and each voter votes exclusively for all of the candidates within a single group, then PAV will act in the same way as theD'Hondt method
The D'Hondt method, also called the Jefferson method or the greatest divisors method, is a method for allocating seats in parliaments among federal states, or in party-list proportional representation systems. It belongs to the class of highest- ...
of party-list proportional representation
Party-list proportional representation (list-PR) is a subset of proportional representation electoral systems in which multiple candidates are elected (e.g., elections to parliament) through their position on an electoral list. They can also be us ...
.
Properties
This section describes axiomatic properties of Proportional Approval Voting.Committees of size one
In an election with only one winner, PAV operates in exactly the same way asapproval voting
Approval voting is an electoral system in which voters can select many candidates instead of selecting only one candidate.
Description
Approval voting ballots show a list of the options of candidates running. Approval voting lets each voter i ...
. That is, it selects the committee consisting of the candidate who is approved by the most voters.
Proportionality
Most systems ofproportional representation
Proportional representation (PR) refers to a type of electoral system under which subgroups of an electorate are reflected proportionately in the elected body. The concept applies mainly to geographical (e.g. states, regions) and political divis ...
use party lists
An electoral list is a grouping of candidates for election, usually found in proportional or mixed electoral systems, but also in some plurality electoral systems. An electoral list can be registered by a political party (a party list) or can ...
. PAV was designed to have both proportional representation and personal votes (voters vote for candidates, not for a party list). It deserves to be called a "proportional" system because if votes turn out to follow a partisan scheme (each voter votes for all candidates from a party and no other) then the system elects a number of candidates in each party that is proportional to the number of voters who chose this party (see Example 2
Example may refer to:
* '' exempli gratia'' (e.g.), usually read out in English as "for example"
* .example, reserved as a domain name that may not be installed as a top-level domain of the Internet
** example.com, example.net, example.org, e ...
). Further, under mild assumptions (symmetry, continuity and Pareto efficiency
Pareto efficiency or Pareto optimality is a situation where no action or allocation is available that makes one individual better off without making another worse off. The concept is named after Vilfredo Pareto (1848–1923), Italian civil engine ...
), PAV is the only extension of the D'Hondt method
The D'Hondt method, also called the Jefferson method or the greatest divisors method, is a method for allocating seats in parliaments among federal states, or in party-list proportional representation systems. It belongs to the class of highest- ...
that allows personal votes and that satisfies the consistency criterion
A voting system is consistent if, whenever the electorate is divided (arbitrarily) into several parts and elections in those parts garner the same result, then an election of the entire electorate also garners that result. Smith calls this property ...
.
Even if the voters do not follow the partisan scheme, the rule provides proportionality guarantees. For example, PAV satisfies the strong fairness property called extended justified representation, as well as the related property proportional justified representation. It also has optimal proportionality degree. All these properties guarantee that any group of voters with cohesive (similar) preferences will be represented by a number of candidates that is at least proportional to the size of the group. It has been shown that PAV is the only method satisfying such properties among all PAV-like optimization methods (that may use numbers other than harmonic numbers in their definition).
The committees returned by PAV might not be in the core
Core or cores may refer to:
Science and technology
* Core (anatomy), everything except the appendages
* Core (manufacturing), used in casting and molding
* Core (optical fiber), the signal-carrying portion of an optical fiber
* Core, the centra ...
, yet---among the known multiwinner voting rules---PAV is closest to satisfying the property. It guarantees 2-approximation of the core, which is the optimal approximation ratio that can be achieved by a rule satisfying the Pigou–Dalton principle The Pigou–Dalton principle (PDP) is a principle in welfare economics, particularly in cardinal welfarism. Named after Arthur Cecil Pigou and Hugh Dalton, it is a condition on social welfare functions. It says that, all other things being equal, a ...
of transfers. Furthermore, PAV satisfies the property of the core if there are sufficiently many similar candidates running in an election.
PAV fails priceability (that is, the choice of PAV cannot be always explained via a process, where the voters are endowed with a fixed amount of virtual money, and spend this spend money on buying candidates they like) and laminar proportionality. Two alternative rules that satisfy priceability and laminar proportionality, and that have comparably good proportionality-related properties to PAV are the Method of Equal Shares
The Method of Equal Shares (in early papers the method has been also referred to as Rule X, but since 2022 the authors started using the name "method of equal shares") is a proportional method of counting ballots that applies to participatory bud ...
and Phragmén's Sequential Rules. These two alternative methods are also computable in polynomial time
In computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by ...
, yet they fail Pareto efficiency
Pareto efficiency or Pareto optimality is a situation where no action or allocation is available that makes one individual better off without making another worse off. The concept is named after Vilfredo Pareto (1848–1923), Italian civil engine ...
.
Other properties
Apart from properties pertaining to proportionality, PAV satisfies the following axioms: *Pareto efficiency
Pareto efficiency or Pareto optimality is a situation where no action or allocation is available that makes one individual better off without making another worse off. The concept is named after Vilfredo Pareto (1848–1923), Italian civil engine ...
,
* Consistency
In classical deductive logic, a consistent theory is one that does not lead to a logical contradiction. The lack of contradiction can be defined in either semantic or syntactic terms. The semantic definition states that a theory is consistent ...
,
* Support monotonicity (if the support of a winning candidate increases, i.e., more voters vote for this candidate, then this candidate remains winning),
* Pigou–Dalton principle The Pigou–Dalton principle (PDP) is a principle in welfare economics, particularly in cardinal welfarism. Named after Arthur Cecil Pigou and Hugh Dalton, it is a condition on social welfare functions. It says that, all other things being equal, a ...
.
PAV fails the following properties:
* House monotonicity
House monotonicity (also called house-size monotonicity) is a property of apportionment methods and multiwinner voting systems. These are methods for allocating seats in a parliament among federal states (or among political party). The property s ...
. Two alternative methods that satisfy house monotonicity and that have comparably good proportionality-related properties to PAV are Sequential Proportional Approval Voting
Sequential proportional approval voting (SPAV) or reweighted approval voting (RAV) is an electoral system that extends the concept of approval voting to a multiple winner election. It is a simplified version of proportional approval voting. Pr ...
and Phragmén's Sequential Rules. These two alternative methods are also computable in polynomial time
In computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by ...
, but they fail Pareto efficiency
Pareto efficiency or Pareto optimality is a situation where no action or allocation is available that makes one individual better off without making another worse off. The concept is named after Vilfredo Pareto (1848–1923), Italian civil engine ...
, Consistency
In classical deductive logic, a consistent theory is one that does not lead to a logical contradiction. The lack of contradiction can be defined in either semantic or syntactic terms. The semantic definition states that a theory is consistent ...
, and the Pigou–Dalton principle The Pigou–Dalton principle (PDP) is a principle in welfare economics, particularly in cardinal welfarism. Named after Arthur Cecil Pigou and Hugh Dalton, it is a condition on social welfare functions. It says that, all other things being equal, a ...
.
Computation
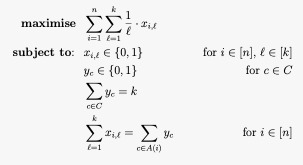 Computing the winning committee under PAV is
Computing the winning committee under PAV is NP-hard
In computational complexity theory, NP-hardness ( non-deterministic polynomial-time hardness) is the defining property of a class of problems that are informally "at least as hard as the hardest problems in NP". A simple example of an NP-hard pr ...
, making it a computationally demanding voting method as the number of candidates and seats increase. Under a brute force approach, if there were ''m'' candidates and ''k'' seats, then there would be
:
combinations of candidates to compare with each election. For example, if there were 24 candidates for 4 seats, there would be 10,626 combinations for which we would need to calculate PAV scores. An election requiring this many calculations would necessitate vote counting by computer. For medium-size elections, the outcome of PAV can be computed by using integer programming
An integer programming problem is a mathematical optimization or Constraint satisfaction problem, feasibility program in which some or all of the variables are restricted to be integers. In many settings the term refers to integer linear programmin ...
solvers. The ILP implementation of PAV is a part of the Python packag''abcvoting''
However, when ''k'' is fixed, the computation of the PAV winning subset is computable in polynomial time, i.e. , where ''n'' is the number of voters.
Sequential proportional approval voting
Sequential proportional approval voting (SPAV) or reweighted approval voting (RAV) is an electoral system that extends the concept of approval voting to a multiple winner election. It is a simplified version of proportional approval voting. Pr ...
is a method that can be considered an approximation
An approximation is anything that is intentionally similar but not exactly equality (mathematics), equal to something else.
Etymology and usage
The word ''approximation'' is derived from Latin ''approximatus'', from ''proximus'' meaning ''very ...
of PAV with approximation ratio equal to , so the PAV score of the resulting committee is at most 37% worse than optimal. This method can be computed in polynomial time, and the election outcome could potentially be determined by hand. Sequential proportional approval voting
Sequential proportional approval voting (SPAV) or reweighted approval voting (RAV) is an electoral system that extends the concept of approval voting to a multiple winner election. It is a simplified version of proportional approval voting. Pr ...
on its own exhibits good properties and can be used as a full-fledged election system, though formally it fails all the proportionality properties that distinguish PAV. A more complex approach based on randomized rounding
Within computer science and operations research,
many combinatorial optimization problems are computationally intractable to solve exactly (to optimality).
Many such problems do admit fast (polynomial time) approximation algorithms—that is, algo ...
gives an approximation ratio of 0.7965. Under standard assumptions in complexity theory, this is the best approximation ratio that can be achieved for PAV in polynomial time. The problem of approximating PAV can be also formulated as the a minimization problem (instead of maximizing we want to minimize ), in which case the best known approximation ratio is 2.36.
From the perspective of parameterized complexity
In computer science, parameterized complexity is a branch of computational complexity theory that focuses on classifying computational problems according to their inherent difficulty with respect to ''multiple'' parameters of the input or output. T ...
, the problem of computing PAV is typically hard, with a few exceptional easy cases. The problem is NP-hard
In computational complexity theory, NP-hardness ( non-deterministic polynomial-time hardness) is the defining property of a class of problems that are informally "at least as hard as the hardest problems in NP". A simple example of an NP-hard pr ...
even in the two-dimensional spatial model of voting. It is solvable in polynomial time in the case of a single dimension.
Beyond approval committee elections
PAV can be used for voting on an agenda consisting of a number of independent issues, on which yes/no decisions need to be made.Further reading
* *See also
*Method of Equal Shares
The Method of Equal Shares (in early papers the method has been also referred to as Rule X, but since 2022 the authors started using the name "method of equal shares") is a proportional method of counting ballots that applies to participatory bud ...
* D'Hondt method
The D'Hondt method, also called the Jefferson method or the greatest divisors method, is a method for allocating seats in parliaments among federal states, or in party-list proportional representation systems. It belongs to the class of highest- ...
* Sequential proportional approval voting
Sequential proportional approval voting (SPAV) or reweighted approval voting (RAV) is an electoral system that extends the concept of approval voting to a multiple winner election. It is a simplified version of proportional approval voting. Pr ...
* Phragmen's voting rules
Phragmén's voting rules are multiwinner voting methods that guarantee proportional representation. They were published by Lars Edvard Phragmén in French and Swedish between 1893 and 1899, and translated to English by Svante Janson in 2016. Ther ...
References
{{voting systems Multi-winner electoral systems Proportional representation electoral systems Approval voting