pole–zero plot on:
[Wikipedia]
[Google]
[Amazon]
In
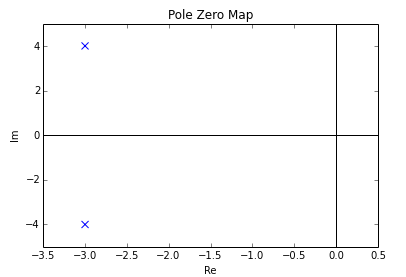 Notice that these two poles are
Notice that these two poles are
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, signal processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, Scalar potential, potential fields, Seismic tomograph ...
and control theory
Control theory is a field of control engineering and applied mathematics that deals with the control system, control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the applic ...
, a pole–zero plot is a graphical representation of a rational
Rationality is the quality of being guided by or based on reason. In this regard, a person acts rationally if they have a good reason for what they do, or a belief is rational if it is based on strong evidence. This quality can apply to an ...
transfer function
In engineering, a transfer function (also known as system function or network function) of a system, sub-system, or component is a function (mathematics), mathematical function that mathematical model, models the system's output for each possible ...
in the complex plane
In mathematics, the complex plane is the plane (geometry), plane formed by the complex numbers, with a Cartesian coordinate system such that the horizontal -axis, called the real axis, is formed by the real numbers, and the vertical -axis, call ...
which helps to convey certain properties of the system such as:
* Stability
* Causal system / anticausal system
* Region of convergence (ROC)
* Minimum phase / non minimum phase
A pole-zero plot shows the location in the complex plane of the poles and zeros of the transfer function
In engineering, a transfer function (also known as system function or network function) of a system, sub-system, or component is a function (mathematics), mathematical function that mathematical model, models the system's output for each possible ...
of a dynamic system, such as a controller, compensator, sensor, equalizer, filter, or communications channel. By convention, the poles of the system are indicated in the plot by an X while the zeros are indicated by a circle or O.
A pole-zero plot is plotted in the plane of a complex frequency domain, which can represent either a continuous-time or a discrete-time system:
* Continuous-time systems use the Laplace transform
In mathematics, the Laplace transform, named after Pierre-Simon Laplace (), is an integral transform that converts a Function (mathematics), function of a Real number, real Variable (mathematics), variable (usually t, in the ''time domain'') to a f ...
and are plotted in the ''s-plane'':
** Real frequency components are along its vertical axis (the imaginary line where )
* Discrete-time systems use the Z-transform and are plotted in the ''z-plane'':
** Real frequency components are along its unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
Continuous-time systems
In general, arational
Rationality is the quality of being guided by or based on reason. In this regard, a person acts rationally if they have a good reason for what they do, or a belief is rational if it is based on strong evidence. This quality can apply to an ...
transfer function for a continuous-time LTI system has the form:
where
* and are polynomials in ,
* is the order of the numerator polynomial,
* is the coefficient of the numerator polynomial,
* is the order of the denominator polynomial, and
* is the coefficient of the denominator polynomial.
Either or or both may be zero, but in real systems, it should be the case that ; otherwise the gain would be unbounded at high frequencies.
Poles and zeros
* the zeros of the system are roots of the numerator polynomial: such that * the poles of the system are roots of the denominator polynomial: such thatRegion of convergence
The region of convergence (ROC) for a given continuous-time transfer function is a half-plane or vertical strip, either of which contains no poles. In general, the ROC is not unique, and the particular ROC in any given case depends on whether the system iscausal
Causality is an influence by which one Event (philosophy), event, process, state, or Object (philosophy), object (''a'' ''cause'') contributes to the production of another event, process, state, or object (an ''effect'') where the cause is at l ...
or anti-causal.
* If the ROC includes the imaginary axis, then the system is bounded-input, bounded-output (BIBO) stable.
* If the ROC extends rightward from the pole with the largest real-part (but not at infinity), then the system is causal.
* If the ROC extends leftward from the pole with the smallest real-part (but not at negative infinity), then the system is anti-causal.
The ROC is usually chosen to include the imaginary axis since it is important for most practical systems to have BIBO stability.
Example
This system has no (finite) zeros and two poles: and The pole-zero plot would be: Notice that these two poles are
Notice that these two poles are complex conjugate
In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign. That is, if a and b are real numbers, then the complex conjugate of a + bi is a - ...
s, which is the necessary and sufficient condition to have real-valued coefficients in the differential equation representing the system.
Discrete-time systems
In general, a rational transfer function for a discrete-time LTI system has the form: where * is the order of the numerator polynomial, * is the coefficient of the numerator polynomial, * is the order of the denominator polynomial, and * is the coefficient of the denominator polynomial. Either or or both may be zero.Poles and zeros
* such that are thezero
0 (zero) is a number representing an empty quantity. Adding (or subtracting) 0 to any number leaves that number unchanged; in mathematical terminology, 0 is the additive identity of the integers, rational numbers, real numbers, and compl ...
s of the system
* such that are the poles of the system.
Region of convergence
The region of convergence (ROC) for a given discrete-time transfer function is a disk or annulus which contains no uncancelled poles. In general, the ROC is not unique, and the particular ROC in any given case depends on whether the system iscausal
Causality is an influence by which one Event (philosophy), event, process, state, or Object (philosophy), object (''a'' ''cause'') contributes to the production of another event, process, state, or object (an ''effect'') where the cause is at l ...
or anti-causal.
* If the ROC includes the unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
, then the system is bounded-input, bounded-output (BIBO) stable.
* If the ROC extends outward from the pole with the largest (but not infinite) magnitude, then the system has a right-sided impulse response. If the ROC extends outward from the pole with the largest magnitude and there is no pole at infinity, then the system is causal.
* If the ROC extends inward from the pole with the smallest (nonzero) magnitude, then the system is anti-causal.
The ROC is usually chosen to include the unit circle since it is important for most practical systems to have BIBO stability.
Example
If and are completely factored, their solution can be easily plotted in the z-plane. For example, given the following transfer function: The only (finite) zero is located at: , and the two poles are located at: , where is theimaginary unit
The imaginary unit or unit imaginary number () is a mathematical constant that is a solution to the quadratic equation Although there is no real number with this property, can be used to extend the real numbers to what are called complex num ...
.
The pole–zero plot would be:
See also
* Root locus *Laplace transform
In mathematics, the Laplace transform, named after Pierre-Simon Laplace (), is an integral transform that converts a Function (mathematics), function of a Real number, real Variable (mathematics), variable (usually t, in the ''time domain'') to a f ...
* Z-transform
* Rational function
In mathematics, a rational function is any function that can be defined by a rational fraction, which is an algebraic fraction such that both the numerator and the denominator are polynomials. The coefficients of the polynomials need not be ...
Bibliography
* * {{DEFAULTSORT:Pole-zero plot Signal processing