perfect powers on:
[Wikipedia]
[Google]
[Amazon]
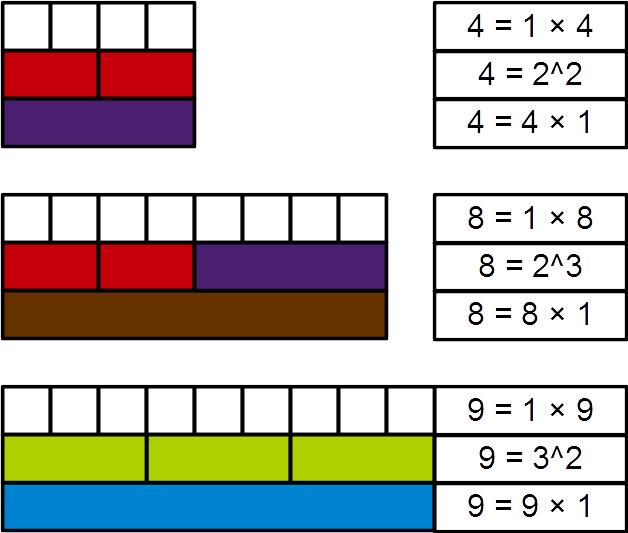 In
In
Lluís Bibiloni, Pelegrí Viader, and Jaume Paradís, On a Series of Goldbach and Euler, 2004 (Pdf)
{{Classes of natural numbers Number theory Integer sequences
 In
In mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, a perfect power is a natural number
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country").
Numbers used for counting are called ''Cardinal n ...
that is a product of equal natural factors, or, in other words, an integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign (−1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language ...
that can be expressed as a square or a higher integer power
Power most often refers to:
* Power (physics), meaning "rate of doing work"
** Engine power, the power put out by an engine
** Electric power
* Power (social and political), the ability to influence people or events
** Abusive power
Power may a ...
of another integer greater than one. More formally, ''n'' is a perfect power if there exist natural number
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country").
Numbers used for counting are called ''Cardinal n ...
s ''m'' > 1, and ''k'' > 1 such that ''mk'' = ''n''. In this case, ''n'' may be called a perfect ''k''th power. If ''k'' = 2 or ''k'' = 3, then ''n'' is called a perfect square or perfect cube
In arithmetic and algebra, the cube of a number is its third power, that is, the result of multiplying three instances of together.
The cube of a number or any other mathematical expression is denoted by a superscript 3, for example or .
...
, respectively. Sometimes 0 and 1 are also considered perfect powers (0''k'' = 0 for any ''k'' > 0, 1''k'' = 1 for any ''k'').
Examples and sums
Asequence
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called ''elements'', or ''terms''). The number of elements (possibly infinite) is calle ...
of perfect powers can be generated by iterating through the possible values for ''m'' and ''k''. The first few ascending perfect powers in numerical order (showing duplicate powers) are :
:
The sum of the reciprocals of the perfect powers (including duplicates such as 34 and 92, both of which equal 81) is 1:
:
which can be proved as follows:
:
The first perfect powers without duplicates are:
:(sometimes 0 and 1), 4, 8, 9, 16, 25, 27, 32, 36, 49, 64, 81, 100, 121, 125, 128, 144, 169, 196, 216, 225, 243, 256, 289, 324, 343, 361, 400, 441, 484, 512, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1000, 1024, ...
The sum of the reciprocals of the perfect powers ''p'' without duplicates is:
:
where μ(''k'') is the Möbius function
The Möbius function is a multiplicative function in number theory introduced by the German mathematician August Ferdinand Möbius (also transliterated ''Moebius'') in 1832. It is ubiquitous in elementary and analytic number theory and most oft ...
and ζ(''k'') is the Riemann zeta function
The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter (zeta), is a mathematical function of a complex variable defined as \zeta(s) = \sum_^\infty \frac = \frac + \frac + \frac + \cdots for \operatorname(s) > ...
.
According to Euler
Leonhard Euler ( , ; 15 April 170718 September 1783) was a Swiss mathematician, physicist, astronomer, geographer, logician and engineer who founded the studies of graph theory and topology and made pioneering and influential discoveries in ma ...
, Goldbach showed (in a now-lost letter) that the sum of over the set of perfect powers ''p'', excluding 1 and excluding duplicates, is 1:
:
This is sometimes known as the Goldbach–Euler theorem
In mathematics, the Goldbach–Euler theorem (also known as Goldbach's theorem), states that the sum of 1/(''p'' − 1) over the set of perfect powers ''p'', excluding 1 and omitting repetitions, converges to 1:
:\sum_^\frac= + \cd ...
.
Detecting perfect powers
Detecting whether or not a given natural number ''n'' is a perfect power may be accomplished in many different ways, with varying levels ofcomplexity
Complexity characterises the behaviour of a system or model whose components interaction, interact in multiple ways and follow local rules, leading to nonlinearity, randomness, collective dynamics, hierarchy, and emergence.
The term is generall ...
. One of the simplest such methods is to consider all possible values for ''k'' across each of the divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer m that may be multiplied by some integer to produce n. In this case, one also says that n is a multiple of m. An integer n is divisible or evenly divisible by ...
s of ''n'', up to . So if the divisors of are then one of the values must be equal to ''n'' if ''n'' is indeed a perfect power.
This method can immediately be simplified by instead considering only prime
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
values of ''k''. This is because if for a composite
Composite or compositing may refer to:
Materials
* Composite material, a material that is made from several different substances
** Metal matrix composite, composed of metal and other parts
** Cermet, a composite of ceramic and metallic materials
...
where ''p'' is prime, then this can simply be rewritten as . Because of this result, the minimal value of ''k'' must necessarily be prime.
If the full factorization of ''n'' is known, say where the are distinct primes, then ''n'' is a perfect power if and only if
In logic and related fields such as mathematics and philosophy, "if and only if" (shortened as "iff") is a biconditional logical connective between statements, where either both statements are true or both are false.
The connective is bicondi ...
where gcd denotes the greatest common divisor
In mathematics, the greatest common divisor (GCD) of two or more integers, which are not all zero, is the largest positive integer that divides each of the integers. For two integers ''x'', ''y'', the greatest common divisor of ''x'' and ''y'' is ...
. As an example, consider ''n'' = 296·360·724. Since gcd(96, 60, 24) = 12, ''n'' is a perfect 12th power (and a perfect 6th power, 4th power, cube and square, since 6, 4, 3 and 2 divide 12).
Gaps between perfect powers
In 2002 Romanian mathematicianPreda Mihăilescu
Preda V. Mihăilescu (born 23 May 1955) is a Romanian mathematician, best known for his proof of the 158-year-old Catalan's conjecture.
Biography
Born in Bucharest,Stewart 2013 he is the brother of Vintilă Mihăilescu.
After leaving Romania in ...
proved that the only pair of consecutive perfect powers is 23 = 8 and 32 = 9, thus proving Catalan's conjecture
Catalan's conjecture (or Mihăilescu's theorem) is a theorem in number theory that was Conjecture, conjectured by the mathematician Eugène Charles Catalan in 1844 and proven in 2002 by Preda Mihăilescu at Paderborn University. The integers 2 ...
.
Pillai's conjecture states that for any given positive integer ''k'' there are only a finite number of pairs of perfect powers whose difference is ''k''. This is an unsolved problem.
See also
*Prime power
In mathematics, a prime power is a positive integer which is a positive integer power of a single prime number.
For example: , and are prime powers, while
, and are not.
The sequence of prime powers begins:
2, 3, 4, 5, 7, 8, 9, 11, 13, 16, 17 ...
References
*External links
Lluís Bibiloni, Pelegrí Viader, and Jaume Paradís, On a Series of Goldbach and Euler, 2004 (Pdf)
{{Classes of natural numbers Number theory Integer sequences