Optimality Theory on:
[Wikipedia]
[Google]
[Amazon]
Optimality theory (frequently abbreviated OT) is a linguistic model proposing that the observed forms of
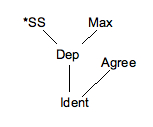 A diagram that represents the necessary rankings of constraints in this style is a Hasse diagram.
A diagram that represents the necessary rankings of constraints in this style is a Hasse diagram.
Ranking & Necessity
ROA-794. * Chomsky (1995). ''The Minimalist Program''. Cambridge, Massachusetts: The MIT Press. * Dresher, Bezalel Elan (1996)
''GLOT International'' 2, 1/2, January/February 1996, page 8 (a humorous introduction for novices) *Hale, Mark, and Charles Reiss (2008). ''The Phonological Enterprise''. Oxford University Press. * Halle, Morris (1995). Feature Geometry and Feature Spreading. ''Linguistic Inquiry'' 26, 1-46. * Heinz, Jeffrey, Greg Kobele, and Jason Riggle (2009)
Evaluating the Complexity of Optimality Theory
''Linguistic Inquiry'' 40, 277–288. * Idsardi, William J. (2006)
A Simple Proof that Optimality Theory is Computationally Intractable
''Linguistic Inquiry'' 37:271-275. * Idsardi, William J. (2000). Clarifying opacity. ''The Linguistic Review'' 17:337-50. * Kager, René (1999). ''Optimality Theory''. Cambridge: Cambridge University Press. * Kornai, Andras (2006)
''Is OT NP-hard?''
ROA-838. * Legendre, Géraldine, Jane Grimshaw and Sten Vikner. (2001). ''Optimality-theoretic Syntax''. MIT Press. * McCarthy, John (2001). ''A Thematic Guide to Optimality Theory''. Cambridge: Cambridge University Press. * McCarthy, John (2007). ''Hidden Generalizations: Phonological Opacity in Optimality Theory''. London: Equinox. * McCarthy, John (2008). ''Doing Optimality Theory: Applying Theory to Data''. Blackwell. * McCarthy, John and Alan Prince (1993)
''Prosodic Morphology: Constraint Interaction and Satisfaction''
Rutgers University Center for Cognitive Science Technical Report 3. * McCarthy, John and Alan Prince (1994)
''The Emergence of the Unmarked: Optimality in Prosodic Morphology''
Proceedings of NELS. * McCarthy, John J. & Alan Prince. (1995)
Faithfulness and reduplicative identity
In J. Beckman, L. W. Dickey, & S. Urbanczyk (Eds.), ''University of Massachusetts occasional papers in linguistics'' (Vol. 18, pp. 249–384). Amherst, Massachusetts: GLSA Publications. * Merchant, Nazarre & Jason Riggle. (2016
OT grammars, beyond partial orders: ERC sets and antimatroids
Nat Lang Linguist Theory, 34: 241. * Moreton, Elliott (2004)
''Non-computable Functions in Optimality Theory''
Ms. from 1999, published 2004 in John J. McCarthy (ed.), ''Optimality Theory in Phonology''. * Pater, Joe. (2009). Weighted Constraints in Generative Linguistics. "Cognitive Science" 33, 999–1035. * Prince, Alan (2007). The Pursuit of Theory. In Paul de Lacy, ed., ''Cambridge Handbook of Phonology''. * Prince, Alan (2002a)
Entailed Ranking Arguments
ROA-500. * Prince, Alan (2002b)
Arguing Optimality
In Coetzee, Andries, Angela Carpenter and Paul de Lacy (eds). ''Papers in Optimality Theory II''. GLSA, UMass. Amherst. ROA-536. * Prince, Alan and Paul Smolensky. (1993/2002/2004): ''Optimality Theory: Constraint Interaction in Generative Grammar''. Blackwell Publishers (2004
2002). Technical Report, Rutgers University Center for Cognitive Science and Computer Science Department, University of Colorado at Boulder (1993). * Tesar, Bruce and Paul Smolensky (1998)
Learnability in Optimality Theory
''Linguistic Inquiry'' 29(2): 229–268. * Trommer, Jochen. (2001)
Distributed Optimality
PhD dissertation, Universität Potsdam. * Wolf, Matthew. (2008)
Optimal Interleaving: Serial Phonology-Morphology Interaction in a Constraint-Based Model
PhD dissertation, University of Massachusetts. ROA-996.
Rutgers University Optimality Archive
Optimality Theory and the Three Laws of Robotics
OT Syntax: an interview with Jane Grimshaw
{{Authority control Optimality Theory, Phonology Phonotactics Phonological theories Linguistics Mathematical linguistics
language
Language is a structured system of communication that consists of grammar and vocabulary. It is the primary means by which humans convey meaning, both in spoken and signed language, signed forms, and may also be conveyed through writing syste ...
arise from the optimal satisfaction of conflicting constraints. OT differs from other approaches to phonological analysis, which typically use rules rather than constraints. However, phonological models of representation, such as autosegmental phonology, prosodic phonology, and linear phonology (SPE), are equally compatible with rule-based and constraint-based models. OT views grammars as systems that provide mappings from inputs to outputs; typically, the inputs are conceived of as underlying representations, and the outputs as their surface realizations. It is an approach within the larger framework of generative grammar
Generative grammar is a research tradition in linguistics that aims to explain the cognitive basis of language by formulating and testing explicit models of humans' subconscious grammatical knowledge. Generative linguists, or generativists (), ...
.
Optimality theory has its origin in a talk given by Alan Prince and Paul Smolensky in 1991 which was later developed in a book manuscript by the same authors in 1993.
Overview
There are three basic components of the theory: * Generator () takes an input, and generates the list of possible outputs, or candidates, * Constraint component () provides the criteria, in the form of strictly ranked violable constraints, used to decide between candidates, and * Evaluator () chooses the optimal candidate based on the constraints, and this candidate is the output. Optimality theory assumes that these components are universal. Differences in grammars reflect different rankings of the universal constraint set, . Part oflanguage acquisition
Language acquisition is the process by which humans acquire the capacity to perceive and comprehend language. In other words, it is how human beings gain the ability to be aware of language, to understand it, and to produce and use words and s ...
can then be described as the process of adjusting the ranking of these constraints.
Optimality theory as applied to language was originally proposed by the linguists Alan Prince and Paul Smolensky in 1991, and later expanded by Prince and John J. McCarthy. Although much of the interest in OT has been associated with its use in phonology
Phonology (formerly also phonemics or phonematics: "phonemics ''n.'' 'obsolescent''1. Any procedure for identifying the phonemes of a language from a corpus of data. 2. (formerly also phonematics) A former synonym for phonology, often pre ...
, the area to which OT was first applied, the theory is also applicable to other subfields of linguistics
Linguistics is the scientific study of language. The areas of linguistic analysis are syntax (rules governing the structure of sentences), semantics (meaning), Morphology (linguistics), morphology (structure of words), phonetics (speech sounds ...
(e.g. syntax
In linguistics, syntax ( ) is the study of how words and morphemes combine to form larger units such as phrases and sentences. Central concerns of syntax include word order, grammatical relations, hierarchical sentence structure (constituenc ...
and semantics
Semantics is the study of linguistic Meaning (philosophy), meaning. It examines what meaning is, how words get their meaning, and how the meaning of a complex expression depends on its parts. Part of this process involves the distinction betwee ...
).
Optimality theory is like other theories of generative grammar
Generative grammar is a research tradition in linguistics that aims to explain the cognitive basis of language by formulating and testing explicit models of humans' subconscious grammatical knowledge. Generative linguists, or generativists (), ...
in its focus on the investigation of universal principles, linguistic typology
Linguistic typology (or language typology) is a field of linguistics that studies and classifies languages according to their structural features to allow their comparison. Its aim is to describe and explain the structural diversity and the co ...
and language acquisition
Language acquisition is the process by which humans acquire the capacity to perceive and comprehend language. In other words, it is how human beings gain the ability to be aware of language, to understand it, and to produce and use words and s ...
.
Optimality theory also has roots in neural network research. It arose in part as an alternative to the connectionist theory of harmonic grammar, developed in 1990 by Géraldine Legendre, Yoshiro Miyata and Paul Smolensky. Variants of OT with connectionist-like weighted constraints continue to be pursued in more recent work (Pater 2009).
Input and : the candidate set
Optimality theory supposes that there are no language-specific restrictions on the input. This is called "richness of the base". Every grammar can handle every possible input. For example, a language without complex clusters must be able to deal with an input such as . Languages without complex clusters differ on how they will resolve this problem; some will epenthesize (e.g. , or if all codas are banned) and some will delete (e.g. ). is free to generate any number of output candidates, however much they deviate from the input. This is called "freedom of analysis". The grammar (ranking of constraints) of the language determines which of the candidates will be assessed as optimal by .: the constraint set
In optimality theory, every constraint is universal. is the same in every language. There are two basic types of constraints: * Faithfulness constraints require that the observed surface form (the output) match the underlying or lexical form (the input) in some particular way; that is, these constraints require identity between input and output forms. * Markedness constraints impose requirements on the structural well-formedness of the output. Each plays a crucial role in the theory. Markedness constraints motivate changes from the underlying form, and faithfulness constraints prevent every input from being realized as some completely unmarked form (such as ). The universal nature of makes some immediate predictions about language typology. If grammars differ only by having different rankings of , then the set of possible human languages is determined by the constraints that exist. Optimality theory predicts that there cannot be more grammars than there are permutations of the ranking of . The number of possible rankings is equal to thefactorial
In mathematics, the factorial of a non-negative denoted is the Product (mathematics), product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial:
\begin
n! &= n \times ...
of the total number of constraints, thus giving rise to the term ''factorial typology''. However, it may not be possible to distinguish all of these potential grammars, since not every constraint is guaranteed to have an observable effect in every language. Two total orders on the constraints of could generate the same range of input–output mappings, but differ in the relative ranking of two constraints which do not conflict with each other. Since there is no way to distinguish these two rankings they are said to belong to the same grammar. A grammar in OT is equivalent to an antimatroid. If rankings with ties are allowed, then the number of possibilities is an ordered Bell number rather than a factorial, allowing a significantly larger number of possibilities.
Faithfulness constraints
McCarthy and Prince (1995) propose three basic families of faithfulness constraints: * prohibits deletion (from "maximal"). * prohibits epenthesis (from "dependent"). * (F) prohibits alteration to the value of feature F (from "identical"). Each of the constraints' names may be suffixed with "-IO" or "-BR", standing for ''input/output'' and ''base/reduplicant'', respectively—the latter of which is used in analysis of reduplication—if desired. ''F'' in (F) is substituted by the name of adistinctive feature
In linguistics, a distinctive feature is the most basic unit of phonology, phonological structure that distinguishes one Phone (phonetics), sound from another within a language. For example, the feature Voice (phonetics), voice''distinguishes ...
, as in (voice).
and replace and proposed by Prince and Smolensky (1993), which stated "underlying segments must be parsed into syllable structure" and "syllable positions must be filled with underlying segments", respectively. and serve essentially the same functions as and , but differ in that they evaluate only the output and not the relation between the input and output, which is rather characteristic of markedness constraints. This stems from the model adopted by Prince and Smolensky known as ''containment theory'', which assumes the input segments unrealized by the output are not removed but rather "left unparsed" by a syllable. The model put forth by McCarthy and Prince (1995, 1999), known as ''correspondence theory'', has since replaced it as the standard framework.
McCarthy and Prince (1995) also propose:
* , violated when a word- or morpheme-internal segment is deleted (from "input-contiguity")
* , violated when a segment is inserted word- or morpheme-internally (from "output-contiguity")
* , violated when the order of some segments is changed (i.e. prohibits metathesis)
* , violated when two or more segments are realized as one (i.e. prohibits fusion)
* , violated when a segment is realized as multiple segments (i.e. prohibits unpacking or vowel breaking—opposite of )
Markedness constraints
Markedness constraints introduced by Prince and Smolensky (1993) include: Precise definitions in literature vary. Some constraints are sometimes used as a "cover constraint", standing in for a set of constraints that are not fully known or important. Some markedness constraints are context-free and others are context-sensitive. For example, *Vnasal states that vowels must not be nasal in any position and is thus context-free, whereas *VoralN states that vowels must not be oral when preceding a tautosyllabic nasal and is thus context-sensitive.Alignment constraints
Local conjunctions
Two constraints may be conjoined as a single constraint, called a ''local conjunction'', which gives only one violation each time both constraints are violated within a given domain, such as a segment, syllable or word. For example, []segment is violated once per voiced obstruent in a coda ("VOP" stands for "voiced obstruent prohibition"), and may be equivalently written as . Local conjunctions are used as a way of circumventing the problem of phonological opacity that arises when analyzing chain shifts.: definition of optimality
In the original proposal, given two candidates, A and B, A is better, or more "harmonic", than B on a constraint if A incurs fewer violations than B. Candidate A is more harmonic than B on an entire constraint hierarchy if A incurs fewer violations of the highest-ranked constraint distinguishing A and B. A is "optimal" in its candidate set if it is better on the constraint hierarchy than all other candidates. However, this definition of is able to model relations that exceed regularity. For example, given the constraints C1, C2, and C3, where C1 dominates C2, which dominates C3 (C1 ≫ C2 ≫ C3), A beats B, or is more harmonic than B, if A has fewer violations than B on the highest ranking constraint which assigns them a different number of violations (A is "optimal" if A beats B and the candidate set comprises only A and B). If A and B tie on C1, but A does better than B on C2, A is optimal, even if A has however many more violations of C3 than B does. This comparison is often illustrated with a tableau. The pointing finger marks the optimal candidate, and each cell displays an asterisk for each violation for a given candidate and constraint. Once a candidate does worse than another candidate on the highest ranking constraint distinguishing them, it incurs a fatal violation (marked in the tableau by an exclamation mark and by shaded cells for the lower-ranked constraints). Once a candidate incurs a fatal violation, it cannot be optimal, even if it outperforms the other candidates on the rest of . Other notational conventions include dotted lines separating columns of unranked or equally ranked constraints, a check mark ✔ in place of a finger in tentatively ranked tableaux (denoting harmonic but not conclusively optimal), and a circled asterisk ⊛ denoting a violation by a winner; in output candidates, the angle brackets denote segments elided in phonetic realization, and □ and □́ denote an epenthetic consonant and vowel, respectively. The "much greater than" sign ≫ (sometimes the nested ⪢) denotes the domination of a constraint over another ("C1 ≫ C2" = "C1 dominates C2") while the "succeeds" operator ≻ denotes superior harmony in comparison of output candidates ("A ≻ B" = "A is more harmonic than B"). Constraints are ranked in a hierarchy of strict domination. The ''strictness of strict domination'' means that a candidate which violates only a high-ranked constraint does worse on the hierarchy than one that does not, even if the second candidate fared worse on every other lower-ranked constraint. This also means that constraints are violable; the winning (i.e. the most harmonic) candidate need not satisfy all constraints, as long as for any rival candidate that does better than the winner on some constraint, there is a higher-ranked constraint on which the winner does better than that rival. Within a language, a constraint may be ranked high enough that it is always obeyed; it may be ranked low enough that it has no observable effects; or, it may have some intermediate ranking. The term ''the emergence of the unmarked'' describes situations in which a markedness constraint has an intermediate ranking, so that it is violated in some forms, but nonetheless has observable effects when higher-ranked constraints are irrelevant. An early example proposed by McCarthy and Prince (1994) is the constraint , which prohibits syllables from ending in consonants. In Balangao, is not ranked high enough to be always obeyed, as witnessed in roots like ''taynan'' (faithfulness to the input prevents deletion of the final ). But, in the reduplicated form ''ma-tayna-taynan'' 'repeatedly be left behind', the final is not copied. Under McCarthy and Prince's analysis, this is because faithfulness to the input does not apply to reduplicated material, and is thus free to prefer ''ma-tayna-taynan'' over hypothetical ''ma-taynan-taynan'' (which has an additional violation of ). Some optimality theorists prefer the use of comparative tableaux, as described in Prince (2002b). Comparative tableaux display the same information as the classic or "flyspeck" tableaux, but the information is presented in such a way that it highlights the most crucial information. For instance, the tableau above would be rendered in the following way. Each row in a comparative tableau represents a winner–loser pair, rather than an individual candidate. In the cells where the constraints assess the winner–loser pairs, "W" is placed if the constraint in that column prefers the winner, "L" if the constraint prefers the loser, and "e" if the constraint does not differentiate between the pair. Presenting the data in this way makes it easier to make generalizations. For instance, in order to have a consistent ranking ''some'' W must dominate ''all'' L's. Brasoveanu and Prince (2005) describe a process known as fusion and the various ways of presenting data in a comparative tableau in order to achieve the necessary and sufficient conditions for a given argument.Example
As a simplified example, consider the manifestation of the English plural: * (''dogs'') * (''cats'') * (''dishes'') Also consider the following constraint set, in descending order of domination: No matter how the constraints are re-ordered, the allomorph will always lose to . This is called ''harmonic bounding''. The violations incurred by the candidate are a subset of the violations incurred by ; specifically, if you epenthesize a vowel, changing the voicing of the morpheme is a gratuitous violation of constraints. In the tableau, there is a candidate which incurs no violations whatsoever. Within the constraint set of the problem, harmonically bounds all other possible candidates. This shows that a candidate does not need to be a winner in order to harmonically bound another candidate. The tableaux from above are repeated below using the comparative tableaux format. From the comparative tableau for , it can be observed that any ranking of these constraints will produce the observed output . Because there are no loser-preferring comparisons, wins under any ranking of these constraints; this means that no ranking can be established on the basis of this input. The tableau for contains rows with a single W and a single L. This shows that , , and must all dominate ; however, no ranking can be established between those constraints on the basis of this input. Based on this tableau, the following ranking has been established: : , , ≫ The tableau for shows that several more rankings are necessary in order to predict the desired outcome. The third row says nothing; there is no loser-preferring comparison in the third row. The first row reveals that either *SS or must dominate , based on the comparison between and . The fourth row shows that must dominate . The second row shows that either *SS or must dominate . From the tableau, it was established that dominates ; this means that *SS must dominate . So far, the following rankings have been shown to be necessary: : *SS, ≫ ≫ While it is possible that can dominate , it is not necessary; the ranking given above is sufficient for the observed to emerge. When the rankings from the tableaux are combined, the following ranking summary can be given: : *SS, ≫ , ≫ ::or : *SS, , ≫ ≫ There are two possible places to put when writing out rankings linearly; neither is truly accurate. The first implies that *SS and must dominate , and the second implies that must dominate . Neither of these are truthful, which is a failing of writing out rankings in a linear fashion like this. These sorts of problems are the reason why most linguists utilize a lattice graph to represent necessary and sufficient rankings, as shown below. A diagram that represents the necessary rankings of constraints in this style is a Hasse diagram.
A diagram that represents the necessary rankings of constraints in this style is a Hasse diagram.
Criticism
Optimality theory has attracted substantial amounts of criticism, most of which is directed at its application to phonology (rather than syntax or other fields). It is claimed that OT cannot account for phonological opacity (see Idsardi 2000, for example). In derivational phonology, effects that are inexplicable at the surface level but are explainable through "opaque" rule ordering may be seen; but in OT, which has no intermediate levels for rules to operate on, these effects are difficult to explain. For example, inQuebec French
Quebec French ( ), also known as Québécois French, is the predominant variety (linguistics), variety of the French language spoken in Canada. It is the dominant language of the province of Quebec, used in everyday communication, in education, ...
, high front vowels triggered affrication of , (e.g. ), but the loss of high vowels (visible at the surface level) has left the affrication with no apparent source. Derivational phonology can explain this by stating that vowel syncope (the loss of the vowel) "counterbled" affrication—that is, instead of vowel syncope occurring and " bleeding" (i.e. preventing) affrication, it says that affrication applies before vowel syncope, so that the high vowel is removed and the environment destroyed which had triggered affrication. Such counterbleeding rule orderings are therefore termed ''opaque'' (as opposed to ''transparent''), because their effects are not visible at the surface level.
The opacity of such phenomena finds no straightforward explanation in OT, since theoretical intermediate forms are not accessible (constraints refer only to the surface form and/or the underlying form). There have been a number of proposals designed to account for it, but most of the proposals significantly alter OT's basic architecture and therefore tend to be highly controversial. Frequently, such alterations add new types of constraints (which are not universal faithfulness or markedness constraints), or change the properties of (such as allowing for serial derivations) or . Examples of these include John J. McCarthy's sympathy theory and candidate chains theory.
A relevant issue is the existence of circular chain shifts, i.e. cases where input maps to output , but input maps to output . Many versions of OT predict this to be impossible (see Moreton 2004, Prince 2007).
Optimality theory is also criticized as being an impossible model of speech production/perception: computing and comparing an infinite number of possible candidates would take an infinitely long time to process. Idsardi (2006) argues this position, though other linguists dispute this claim on the grounds that Idsardi makes unreasonable assumptions about the constraint set and candidates, and that more moderate instantiations of OT do not present such significant computational problem
In theoretical computer science, a computational problem is one that asks for a solution in terms of an algorithm. For example, the problem of factoring
:"Given a positive integer ''n'', find a nontrivial prime factor of ''n''."
is a computati ...
s (see Kornai (2006) and Heinz, Kobele and Riggle (2009)). Another common rebuttal to this criticism of OT is that the framework is purely representational. In this view, OT is taken to be a model of linguistic competence and is therefore not intended to explain the specifics of linguistic performance.
Another objection to OT is that it is not technically a theory, in that it does not make falsifiable predictions. The source of this issue may be in terminology: the term ''theory'' is used differently here than in physics, chemistry, and other sciences. Specific instantiations of OT may make falsifiable predictions, in the same way specific proposals within other linguistic frameworks can. What predictions are made, and whether they are testable, depends on the specifics of individual proposals (most commonly, this is a matter of the definitions of the constraints used in an analysis). Thus, OT as a framework is best described as a scientific paradigm.
Theories within optimality theory
In practice, implementations of OT often make use of many concepts of phonological theories of representations, such as thesyllable
A syllable is a basic unit of organization within a sequence of speech sounds, such as within a word, typically defined by linguists as a ''nucleus'' (most often a vowel) with optional sounds before or after that nucleus (''margins'', which are ...
, the mora, or feature geometry. Completely distinct from these, there are sub-theories which have been proposed entirely within OT, such as positional faithfulness theory, correspondence theory (McCarthy and Prince 1995), sympathy theory, stratal OT, and a number of theories of learnability, most notably by Bruce Tesar. Other theories within OT are concerned with issues like the need for derivational levels within the phonological domain, the possible formulations of constraints, and constraint interactions other than strict domination.
Use outside of phonology
Optimality theory is most commonly associated with the field ofphonology
Phonology (formerly also phonemics or phonematics: "phonemics ''n.'' 'obsolescent''1. Any procedure for identifying the phonemes of a language from a corpus of data. 2. (formerly also phonematics) A former synonym for phonology, often pre ...
, but has also been applied to other areas of linguistics. Jane Grimshaw, Geraldine Legendre and Joan Bresnan have developed instantiations of the theory within syntax
In linguistics, syntax ( ) is the study of how words and morphemes combine to form larger units such as phrases and sentences. Central concerns of syntax include word order, grammatical relations, hierarchical sentence structure (constituenc ...
. Optimality theoretic approaches are also relatively prominent in morphology (and the morphology–phonology interface in particular).
In the domain of semantics
Semantics is the study of linguistic Meaning (philosophy), meaning. It examines what meaning is, how words get their meaning, and how the meaning of a complex expression depends on its parts. Part of this process involves the distinction betwee ...
, OT is less commonly used. But constraint-based systems have been developed to provide a formal model of interpretation. OT has also been used as a framework for pragmatics
In linguistics and the philosophy of language, pragmatics is the study of how Context (linguistics), context contributes to meaning. The field of study evaluates how human language is utilized in social interactions, as well as the relationship ...
.
For orthography
An orthography is a set of convention (norm), conventions for writing a language, including norms of spelling, punctuation, Word#Word boundaries, word boundaries, capitalization, hyphenation, and Emphasis (typography), emphasis.
Most national ...
, constraint-based analyses have also been proposed, among others, by Richard Wiese and Silke Hamann/ Ilaria Colombo. Constraints cover both the relations between sound and letter as well as preferences for spelling itself.
Notes
References
* Brasoveanu, Adrian, and Alan Prince (2005)Ranking & Necessity
ROA-794. * Chomsky (1995). ''The Minimalist Program''. Cambridge, Massachusetts: The MIT Press. * Dresher, Bezalel Elan (1996)
''GLOT International'' 2, 1/2, January/February 1996, page 8 (a humorous introduction for novices) *Hale, Mark, and Charles Reiss (2008). ''The Phonological Enterprise''. Oxford University Press. * Halle, Morris (1995). Feature Geometry and Feature Spreading. ''Linguistic Inquiry'' 26, 1-46. * Heinz, Jeffrey, Greg Kobele, and Jason Riggle (2009)
Evaluating the Complexity of Optimality Theory
''Linguistic Inquiry'' 40, 277–288. * Idsardi, William J. (2006)
A Simple Proof that Optimality Theory is Computationally Intractable
''Linguistic Inquiry'' 37:271-275. * Idsardi, William J. (2000). Clarifying opacity. ''The Linguistic Review'' 17:337-50. * Kager, René (1999). ''Optimality Theory''. Cambridge: Cambridge University Press. * Kornai, Andras (2006)
''Is OT NP-hard?''
ROA-838. * Legendre, Géraldine, Jane Grimshaw and Sten Vikner. (2001). ''Optimality-theoretic Syntax''. MIT Press. * McCarthy, John (2001). ''A Thematic Guide to Optimality Theory''. Cambridge: Cambridge University Press. * McCarthy, John (2007). ''Hidden Generalizations: Phonological Opacity in Optimality Theory''. London: Equinox. * McCarthy, John (2008). ''Doing Optimality Theory: Applying Theory to Data''. Blackwell. * McCarthy, John and Alan Prince (1993)
''Prosodic Morphology: Constraint Interaction and Satisfaction''
Rutgers University Center for Cognitive Science Technical Report 3. * McCarthy, John and Alan Prince (1994)
''The Emergence of the Unmarked: Optimality in Prosodic Morphology''
Proceedings of NELS. * McCarthy, John J. & Alan Prince. (1995)
Faithfulness and reduplicative identity
In J. Beckman, L. W. Dickey, & S. Urbanczyk (Eds.), ''University of Massachusetts occasional papers in linguistics'' (Vol. 18, pp. 249–384). Amherst, Massachusetts: GLSA Publications. * Merchant, Nazarre & Jason Riggle. (2016
OT grammars, beyond partial orders: ERC sets and antimatroids
Nat Lang Linguist Theory, 34: 241. * Moreton, Elliott (2004)
''Non-computable Functions in Optimality Theory''
Ms. from 1999, published 2004 in John J. McCarthy (ed.), ''Optimality Theory in Phonology''. * Pater, Joe. (2009). Weighted Constraints in Generative Linguistics. "Cognitive Science" 33, 999–1035. * Prince, Alan (2007). The Pursuit of Theory. In Paul de Lacy, ed., ''Cambridge Handbook of Phonology''. * Prince, Alan (2002a)
Entailed Ranking Arguments
ROA-500. * Prince, Alan (2002b)
Arguing Optimality
In Coetzee, Andries, Angela Carpenter and Paul de Lacy (eds). ''Papers in Optimality Theory II''. GLSA, UMass. Amherst. ROA-536. * Prince, Alan and Paul Smolensky. (1993/2002/2004): ''Optimality Theory: Constraint Interaction in Generative Grammar''. Blackwell Publishers (2004
2002). Technical Report, Rutgers University Center for Cognitive Science and Computer Science Department, University of Colorado at Boulder (1993). * Tesar, Bruce and Paul Smolensky (1998)
Learnability in Optimality Theory
''Linguistic Inquiry'' 29(2): 229–268. * Trommer, Jochen. (2001)
Distributed Optimality
PhD dissertation, Universität Potsdam. * Wolf, Matthew. (2008)
Optimal Interleaving: Serial Phonology-Morphology Interaction in a Constraint-Based Model
PhD dissertation, University of Massachusetts. ROA-996.
External links
Rutgers University Optimality Archive
Optimality Theory and the Three Laws of Robotics
OT Syntax: an interview with Jane Grimshaw
{{Authority control Optimality Theory, Phonology Phonotactics Phonological theories Linguistics Mathematical linguistics