Order-sorted Logic on:
[Wikipedia]
[Google]
[Amazon]
Many-sorted logic can reflect formally our intention not to handle the universe as a
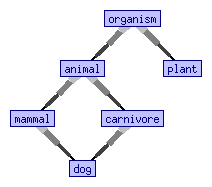 While ''many-sorted'' logic requires two distinct sorts to have disjoint universe sets, ''order-sorted'' logic allows one sort to be declared a subsort of another sort , usually by writing or similar syntax. In the above biology example, it is desirable to declare
:,
:,
:,
:,
:,
:,
and so on; cf. picture.
Wherever a term of some sort is required, a term of any subsort of may be supplied instead (''
While ''many-sorted'' logic requires two distinct sorts to have disjoint universe sets, ''order-sorted'' logic allows one sort to be declared a subsort of another sort , usually by writing or similar syntax. In the above biology example, it is desirable to declare
:,
:,
:,
:,
:,
:,
and so on; cf. picture.
Wherever a term of some sort is required, a term of any subsort of may be supplied instead (''
''Lecture Notes on Decision Procedures''
b
Calogero G. Zarba
Systems of formal logic
homogeneous
Homogeneity and heterogeneity are concepts often used in the sciences and statistics relating to the uniformity of a substance or organism. A material or image that is homogeneous is uniform in composition or character (i.e. color, shape, siz ...
collection of objects, but to partition it in a way that is similar to types in typeful programming. Both functional and assertive "parts of speech
In grammar, a part of speech or part-of-speech (abbreviated as POS or PoS, also known as word class or grammatical category) is a category of words (or, more generally, of lexical items) that have similar grammatical properties. Words that are assi ...
" in the language of the logic reflect this typeful partitioning of the universe, even on the syntax level: substitution and argument passing can be done only accordingly, respecting the "sorts".
There are various ways to formalize the intention mentioned above; a ''many-sorted logic'' is any package of information which fulfils it. In most cases, the following are given:
* a set of sorts, ''S''
* an appropriate generalization of the notion of ''signature
A signature (; from la, signare, "to sign") is a Handwriting, handwritten (and often Stylization, stylized) depiction of someone's name, nickname, or even a simple "X" or other mark that a person writes on documents as a proof of identity and ...
'' to be able to handle the additional information that comes with the sorts.
The domain of discourse
In the formal sciences, the domain of discourse, also called the universe of discourse, universal set, or simply universe, is the set of entities over which certain variables of interest in some formal treatment may range.
Overview
The dom ...
of any structure of that signature is then fragmented into disjoint subsets, one for every sort.
Example
When reasoning about biological organisms, it is useful to distinguish two sorts: and . While a function makes sense, a similar function usually does not. Many-sorted logic allows one to have terms like , but to discard terms like as syntactically ill-formed.Algebraization
The algebraization of many-sorted logic is explained in an article by Caleiro and Gonçalves, which generalizesabstract algebraic logic
In mathematical logic, abstract algebraic logic is the study of the algebraization of deductive systems
arising as an abstraction of the well-known Lindenbaum–Tarski algebra, and how the resulting algebras are related to logical systems.Font, 200 ...
to the many-sorted case, but can also be used as introductory material.
Order-sorted logic
 While ''many-sorted'' logic requires two distinct sorts to have disjoint universe sets, ''order-sorted'' logic allows one sort to be declared a subsort of another sort , usually by writing or similar syntax. In the above biology example, it is desirable to declare
:,
:,
:,
:,
:,
:,
and so on; cf. picture.
Wherever a term of some sort is required, a term of any subsort of may be supplied instead (''
While ''many-sorted'' logic requires two distinct sorts to have disjoint universe sets, ''order-sorted'' logic allows one sort to be declared a subsort of another sort , usually by writing or similar syntax. In the above biology example, it is desirable to declare
:,
:,
:,
:,
:,
:,
and so on; cf. picture.
Wherever a term of some sort is required, a term of any subsort of may be supplied instead (''Liskov substitution principle
The Liskov substitution principle (LSP) is a particular definition of a subtyping relation, called strong behavioral subtyping, that was initially introduced by Barbara Liskov in a 1988 conference keynote address titled ''Data abstraction and h ...
''). For example, assuming a function declaration , and a constant declaration , the term is perfectly valid and has the sort . In order to supply the information that the mother of a dog is a dog in turn, another declaration may be issued; this is called ''function overloading'', similar to overloading in programming languages
In programming language theory and type theory, polymorphism is the provision of a single interface to entities of different types or the use of a single symbol to represent multiple different types.: "Polymorphic types are types whose operation ...
.
Order-sorted logic can be translated into unsorted logic, using a unary predicate for each sort , and an axiom for each subsort declaration . The reverse approach was successful in automated theorem proving: in 1985, Christoph Walther could solve a then benchmark problem by translating it into order-sorted logic, thereby boiling it down an order of magnitude, as many unary predicates turned into sorts.
In order to incorporate order-sorted logic into a clause-based automated theorem prover, a corresponding '' order-sorted unification'' algorithm is necessary, which requires for any two declared sorts their intersection to be declared, too: if and are variables of sort and , respectively, the equation has the solution , where .
Smolka generalized order-sorted logic to allow for parametric polymorphism
In programming languages and type theory, parametric polymorphism allows a single piece of code to be given a "generic" type, using variables in place of actual types, and then instantiated with particular types as needed. Parametrically polymorph ...
.
In his framework, subsort declarations are propagated to complex type expressions.
As a programming example, a parametric sort may be declared (with being a type parameter as in a C++ template
C, or c, is the third letter in the Latin alphabet, used in the modern English alphabet, the alphabets of other western European languages and others worldwide. Its name in English is ''cee'' (pronounced ), plural ''cees''.
History
"C" ...
), and from a subsort declaration the relation is automatically inferred, meaning that each list of integers is also a list of floats.
Schmidt-Schauß generalized order-sorted logic to allow for term declarations.
As an example, assuming subsort declarations and , a term declaration like allows to declare a property of integer addition that could not be expressed by ordinary overloading.
See also
*Categorical logic
__NOTOC__
Categorical logic is the branch of mathematics in which tools and concepts from category theory are applied to the study of mathematical logic. It is also notable for its connections to theoretical computer science.
In broad terms, cat ...
* Many-sorted first-order logic#Many-sorted logic
References
Early papers on many-sorted logic include: * , collected in the author's ''Computation, Logic, Philosophy. A Collection of Essays'', Beijing: Science Press; Dordrecht: Kluwer Academic, 1990. * * * {{cite journal, author=F. Jeffry Pelletier, title=Sortal Quantification and Restricted Quantification, journal=Philosophical Studies, year=1972, volume=23, issue=6, pages=400–404, url=https://www.sfu.ca/~jeffpell/papers/SortalRestrQuant.pdf, doi=10.1007/bf00355532, s2cid=170303654External links
*"Many-sorted Logic", the first chapter i''Lecture Notes on Decision Procedures''
b
Calogero G. Zarba
Systems of formal logic