One-way quantum computer on:
[Wikipedia]
[Google]
[Amazon]

 In the quantum logic gate model, a set of qubits, called register, is prepared at the beginning of the computation, then a set of logic operations over the qubits, carried by unitary operators, is implemented. A quantum circuit is formed by a register of qubits on which unitary transformations are applied over the qubits. In the measurement-based quantum computation, instead of implementing a logic operation via unitary transformations, the same operation is executed by entangling a number of input qubits with a cluster of ancillary qubits, forming an overall source state of qubits, and then measuring a number of them. The remaining output qubits will be affected by the measurements because of the entanglement with the measured qubits. The one-way computer has been proved to be a universal quantum computer, which means it can reproduce any unitary operation over an arbitrary number of qubits.
In the quantum logic gate model, a set of qubits, called register, is prepared at the beginning of the computation, then a set of logic operations over the qubits, carried by unitary operators, is implemented. A quantum circuit is formed by a register of qubits on which unitary transformations are applied over the qubits. In the measurement-based quantum computation, instead of implementing a logic operation via unitary transformations, the same operation is executed by entangling a number of input qubits with a cluster of ancillary qubits, forming an overall source state of qubits, and then measuring a number of them. The remaining output qubits will be affected by the measurements because of the entanglement with the measured qubits. The one-way computer has been proved to be a universal quantum computer, which means it can reproduce any unitary operation over an arbitrary number of qubits.
 At the beginning of the computation, the qubits can be distinguished into two categories: the input and the ancillary qubits. The inputs represent the qubits set in a generic state, on which some unitary transformations are to be acted. In order to prepare the source state, all the ancillary qubits must be prepared in the state:
:
where and are the quantum encoding for the classical and bits:
:.
A register with qubits will be therefore set as . Thereafter, the entanglement between two qubits can be performed by applying a gate operation. The matrix representation of such two-qubits operator is given by
:
The action of a gate over two qubits can be described by the following system:
:
When applying a gate over two ancillae in the state, the overall state
:
turns to be an entangled pair of qubits. When entangling two ancillae, no importance is given about which is the control qubit and which one the target, as far as the outcome turns to be the same. Similarly, as the gates are represented in a diagonal form, they all commute each other, and no importance is given about which qubits to entangle first. Photons are the most common source to prepare entangled physical qubits.
At the beginning of the computation, the qubits can be distinguished into two categories: the input and the ancillary qubits. The inputs represent the qubits set in a generic state, on which some unitary transformations are to be acted. In order to prepare the source state, all the ancillary qubits must be prepared in the state:
:
where and are the quantum encoding for the classical and bits:
:.
A register with qubits will be therefore set as . Thereafter, the entanglement between two qubits can be performed by applying a gate operation. The matrix representation of such two-qubits operator is given by
:
The action of a gate over two qubits can be described by the following system:
:
When applying a gate over two ancillae in the state, the overall state
:
turns to be an entangled pair of qubits. When entangling two ancillae, no importance is given about which is the control qubit and which one the target, as far as the outcome turns to be the same. Similarly, as the gates are represented in a diagonal form, they all commute each other, and no importance is given about which qubits to entangle first. Photons are the most common source to prepare entangled physical qubits.
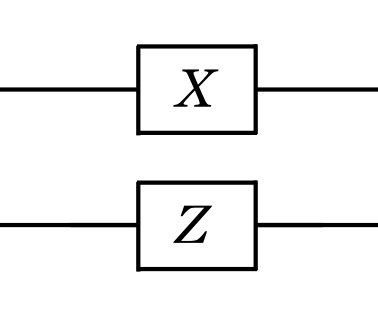 The process of measurement over a single-particle state can be described by projecting the state on the eigenvector of an observable. Consider an observable with two possible eigenvectors, say and , and suppose to deal with a multi-particle quantum system . Measuring the -th qubit by the observable means to project the state over the eigenvectors of :
:.
The actual state of the -th qubit is now , which can turn to be or , depending on the outcome from the measurement (which is probabilistic in quantum mechanics). The measurement projection can be performed over the eigenstates of the observable:
:,
where and belong to the
The process of measurement over a single-particle state can be described by projecting the state on the eigenvector of an observable. Consider an observable with two possible eigenvectors, say and , and suppose to deal with a multi-particle quantum system . Measuring the -th qubit by the observable means to project the state over the eigenvectors of :
:.
The actual state of the -th qubit is now , which can turn to be or , depending on the outcome from the measurement (which is probabilistic in quantum mechanics). The measurement projection can be performed over the eigenstates of the observable:
:,
where and belong to the
 The operations of entanglement, measurement and correction can be performed in order to implement unitary gates. Such operations can be performed time by time for any logic gate in the circuit, or rather in a pattern which allocates all the entanglement operations at the beginning, the measurements in the middle and the corrections at the end of the circuit. Such pattern of computation is referred to as ''CME'' standard pattern. In the ''CME'' formalism, the operation of entanglement between the and qubits is referred to as . The measurement on the qubit, in the - plane, with respect to a angle, is defined as . At last, the byproduct over a qubit, with respect to the measurement over a qubit, is described as , where is set to if the outcome is the state, when the outcome is . The same notation holds for the byproducts.
When performing a computation following the ''CME'' pattern, it may happen that two measurements and on the - plane depend one on the outcome from the other. For example, the sign in front of the angle of measurement on the -th qubit can be flipped with respect to the measurement over the -th qubit: in such case, the notation will be written as , and therefore the two operations of measurement do commute each other no more. If is set to , no flip on the sign will occur, otherwise (when ) the angle will be flipped to . The notation can therefore be rewritten as .
The operations of entanglement, measurement and correction can be performed in order to implement unitary gates. Such operations can be performed time by time for any logic gate in the circuit, or rather in a pattern which allocates all the entanglement operations at the beginning, the measurements in the middle and the corrections at the end of the circuit. Such pattern of computation is referred to as ''CME'' standard pattern. In the ''CME'' formalism, the operation of entanglement between the and qubits is referred to as . The measurement on the qubit, in the - plane, with respect to a angle, is defined as . At last, the byproduct over a qubit, with respect to the measurement over a qubit, is described as , where is set to if the outcome is the state, when the outcome is . The same notation holds for the byproducts.
When performing a computation following the ''CME'' pattern, it may happen that two measurements and on the - plane depend one on the outcome from the other. For example, the sign in front of the angle of measurement on the -th qubit can be flipped with respect to the measurement over the -th qubit: in such case, the notation will be written as , and therefore the two operations of measurement do commute each other no more. If is set to , no flip on the sign will occur, otherwise (when ) the angle will be flipped to . The notation can therefore be rewritten as .

quantum computing
Quantum computing is a type of computation whose operations can harness the phenomena of quantum mechanics, such as superposition, interference, and entanglement. Devices that perform quantum computations are known as quantum computers. Thou ...
that first prepares an entangled ''resource state'', usually a cluster state
In quantum information and quantum computing, a cluster state is a type of highly entangled state of multiple qubits. Cluster states are generated in lattices of qubits with Ising type interactions. A cluster ''C'' is a connected subset of a '' ...
or graph state
In quantum computing, a graph state is a special type of multi-qubit state that can be represented by a graph. Each qubit is represented by a vertex of the graph, and there is an edge between every interacting pair of qubits. In particular, they a ...
, then performs single qubit
In quantum computing, a qubit () or quantum bit is a basic unit of quantum information—the quantum version of the classic binary bit physically realized with a two-state device. A qubit is a two-state (or two-level) quantum-mechanical system, ...
measurements on it. It is "one-way" because the resource state is destroyed by the measurements.
The outcome of each individual measurement is random, but they are related in such a way that the computation always succeeds. In general the choices of basis
Basis may refer to:
Finance and accounting
*Adjusted basis, the net cost of an asset after adjusting for various tax-related items
*Basis point, 0.01%, often used in the context of interest rates
* Basis trading, a trading strategy consisting o ...
for later measurements need to depend on the results of earlier measurements, and hence the measurements cannot all be performed at the same time.
The hardware implementation of MBQC mainly relies on photonic devices, thanks to the properties of entanglement between the photons. The process of entanglement and measurement can be described with the help of graph tools and group theory
In abstract algebra, group theory studies the algebraic structures known as group (mathematics), groups.
The concept of a group is central to abstract algebra: other well-known algebraic structures, such as ring (mathematics), rings, field ...
, in particular by the elements from the stabilizer group.
Definition
The purpose of quantum computing focuses on building an information theory with the features ofquantum mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, q ...
: instead of encoding a binary unit of information (bit
The bit is the most basic unit of information in computing and digital communications. The name is a portmanteau of binary digit. The bit represents a logical state with one of two possible values. These values are most commonly represented a ...
), which can be switched to 1 or 0, a quantum binary unit of information (qubit) can simultaneously turn to be 0 and 1 at the same time, thanks to the phenomenon called superposition. Another key feature for quantum computing relies on the entanglement between the qubits.
 In the quantum logic gate model, a set of qubits, called register, is prepared at the beginning of the computation, then a set of logic operations over the qubits, carried by unitary operators, is implemented. A quantum circuit is formed by a register of qubits on which unitary transformations are applied over the qubits. In the measurement-based quantum computation, instead of implementing a logic operation via unitary transformations, the same operation is executed by entangling a number of input qubits with a cluster of ancillary qubits, forming an overall source state of qubits, and then measuring a number of them. The remaining output qubits will be affected by the measurements because of the entanglement with the measured qubits. The one-way computer has been proved to be a universal quantum computer, which means it can reproduce any unitary operation over an arbitrary number of qubits.
In the quantum logic gate model, a set of qubits, called register, is prepared at the beginning of the computation, then a set of logic operations over the qubits, carried by unitary operators, is implemented. A quantum circuit is formed by a register of qubits on which unitary transformations are applied over the qubits. In the measurement-based quantum computation, instead of implementing a logic operation via unitary transformations, the same operation is executed by entangling a number of input qubits with a cluster of ancillary qubits, forming an overall source state of qubits, and then measuring a number of them. The remaining output qubits will be affected by the measurements because of the entanglement with the measured qubits. The one-way computer has been proved to be a universal quantum computer, which means it can reproduce any unitary operation over an arbitrary number of qubits.
General procedure
The standard process of measurement-based quantum computing consists of three steps: entangle the qubits, measure the ancillae (auxiliary qubits) and correct the outputs. In the first step, the qubits are entangled in order to prepare the source state. In the second step, the ancillae are measured, affecting the state of the output qubits. However, the measurement outputs are non-deterministic result, due to undetermined nature of quantum mechanics: in order to carry on the computation in a deterministic way, some correction operators, called byproducts, are introduced.Preparing the source state
Measuring the qubits
 The process of measurement over a single-particle state can be described by projecting the state on the eigenvector of an observable. Consider an observable with two possible eigenvectors, say and , and suppose to deal with a multi-particle quantum system . Measuring the -th qubit by the observable means to project the state over the eigenvectors of :
:.
The actual state of the -th qubit is now , which can turn to be or , depending on the outcome from the measurement (which is probabilistic in quantum mechanics). The measurement projection can be performed over the eigenstates of the observable:
:,
where and belong to the
The process of measurement over a single-particle state can be described by projecting the state on the eigenvector of an observable. Consider an observable with two possible eigenvectors, say and , and suppose to deal with a multi-particle quantum system . Measuring the -th qubit by the observable means to project the state over the eigenvectors of :
:.
The actual state of the -th qubit is now , which can turn to be or , depending on the outcome from the measurement (which is probabilistic in quantum mechanics). The measurement projection can be performed over the eigenstates of the observable:
:,
where and belong to the Pauli matrices
In mathematical physics and mathematics, the Pauli matrices are a set of three complex matrices which are Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma (), they are occasionally denoted by tau () when use ...
. The eigenvectors of are . Measuring a qubit on the - plane, i.e. by the observable, means to project it over or . In the one-way quantum computing, once a qubit has been measured, there is no way to recycle it in the flow of computation. Therefore, instead of using the notation, it is common to find to indicate a projective measurement over the -th qubit.
Correcting the output
After all the measurements have been performed, the system has been reduced to a smaller number of qubits, which form the output state of the system. Due to the probabilistic outcome of measurements, the system is not set in a deterministic way: after a measurement on the - plane, the output may change whether the outcome had been or . In order to perform a deterministic computation, some corrections must be introduced. The correction operators, or byproduct operators, are applied to the output qubits after all the measurements have been performed. The byproduct operators which can be implemented are and . Depending on the outcome of the measurement, a byproduct operator can be applied or not to the output state: a correction over the -th qubit, depending on the outcome of the measurement performed over the -th qubit via the observable, can be described as , where is set to be if the outcome of measurement was , otherwise is if it was . In the first case, no correction will occur, in the latter one a operator will be implemented on the -th qubit. Eventually, even though the outcome of a measurement is not deterministic in quantum mechanics, the results from measurements can be used in order to perform corrections, and carry on a deterministic computation.''CME'' pattern
 The operations of entanglement, measurement and correction can be performed in order to implement unitary gates. Such operations can be performed time by time for any logic gate in the circuit, or rather in a pattern which allocates all the entanglement operations at the beginning, the measurements in the middle and the corrections at the end of the circuit. Such pattern of computation is referred to as ''CME'' standard pattern. In the ''CME'' formalism, the operation of entanglement between the and qubits is referred to as . The measurement on the qubit, in the - plane, with respect to a angle, is defined as . At last, the byproduct over a qubit, with respect to the measurement over a qubit, is described as , where is set to if the outcome is the state, when the outcome is . The same notation holds for the byproducts.
When performing a computation following the ''CME'' pattern, it may happen that two measurements and on the - plane depend one on the outcome from the other. For example, the sign in front of the angle of measurement on the -th qubit can be flipped with respect to the measurement over the -th qubit: in such case, the notation will be written as , and therefore the two operations of measurement do commute each other no more. If is set to , no flip on the sign will occur, otherwise (when ) the angle will be flipped to . The notation can therefore be rewritten as .
The operations of entanglement, measurement and correction can be performed in order to implement unitary gates. Such operations can be performed time by time for any logic gate in the circuit, or rather in a pattern which allocates all the entanglement operations at the beginning, the measurements in the middle and the corrections at the end of the circuit. Such pattern of computation is referred to as ''CME'' standard pattern. In the ''CME'' formalism, the operation of entanglement between the and qubits is referred to as . The measurement on the qubit, in the - plane, with respect to a angle, is defined as . At last, the byproduct over a qubit, with respect to the measurement over a qubit, is described as , where is set to if the outcome is the state, when the outcome is . The same notation holds for the byproducts.
When performing a computation following the ''CME'' pattern, it may happen that two measurements and on the - plane depend one on the outcome from the other. For example, the sign in front of the angle of measurement on the -th qubit can be flipped with respect to the measurement over the -th qubit: in such case, the notation will be written as , and therefore the two operations of measurement do commute each other no more. If is set to , no flip on the sign will occur, otherwise (when ) the angle will be flipped to . The notation can therefore be rewritten as .
An example: Euler rotations
As an illustrative example, consider the Euler rotation in the basis: such operation, in the gate model of quantum computation, is described as :, where are the angles for the rotation, while defines a global phase which is irrelevant for the computation. To perform such operation in the one-way computing frame, it is possible to implement the following ''CME'' pattern: :, where the input state is the qubit , all the other qubits are auxiliary ancillae and therefore have to be prepared in the state. In the first step, the input state must be entangled with the second qubits; in turn, the second qubit must be entangled with the third one and so on. The entangling operations between the qubits can be performed by the gates. In the second place, the first and the second qubits must be measured by the observable, which means they must be projected onto the eigenstates of such observable. When the is zero, the states reduce to ones, i.e. the eigenvectors for the Pauli operator. The first measurement is performed on the qubit with a angle, which means it has to be projected onto the states. The second measurement is performed with respect to the angle, i.e. the second qubit has to be projected on the state. However, if the outcome from the previous measurement has been , the sign of the angle has to be flipped, and the second qubit will be projected to the state; if the outcome from the first measurement has been , no flip needs to be performed. The same operations have to be repeated for the third and the fourth measurements, according to the respective angles and sign flips. The sign over the angle is set to be . Eventually the fifth qubit (the only one not to be measured) figures out to be the output state. At last, the corrections over the output state have to be performed via the byproduct operators. For instance, if the measurements over the second and the fourth qubits turned to be and , no correction will be conducted by the operator, as . The same result holds for a outcome, as and thus the squared Pauli operator returns the identity. As seen in such example, in the measurement-based computation model, the physical input qubit (the first one) and output qubit (the third one) may differ each other.Equivalence between quantum circuit model and MBQC
The one-way quantum computer allows the implementation of a circuit of unitary transformations through the operations of entanglement and measurement. At the same time, any quantum circuit can be in turn converted into a ''CME'' pattern: a technique to translate quantum circuits into a ''MBQC'' pattern of measurements has been formulated by V. Danos et al. Such conversion can be carried on by using a universal set of logic gates composed by the and the operators: therefore, any circuit can be decomposed into a set of and the gates. The single-qubit operator is defined as follows: :. The can be converted into a ''CME'' pattern as follows: : which means, to implement a operator, the input qubits must be entangled with an ancilla qubit , therefore the input must be measured on the - plane, thereafter the output qubit is corrected by the byproduct. Once every gate has been decomposed into the ''CME'' pattern, the operations in the overall computation will consist of entanglements, measurements and corrections. In order to lead the whole flow of computation to a ''CME'' pattern, some rules are provided.Standardization
In order to move all the entanglements at the beginning of the process, some rules ofcommutation
Commute, commutation or commutative may refer to:
* Commuting, the process of travelling between a place of residence and a place of work
Mathematics
* Commutative property, a property of a mathematical operation whose result is insensitive to th ...
must be pointed out:
:
:
:.
The entanglement operator commutes with the Pauli operators and with any other operator acting on a qubit , but not with the Pauli operators acting on the -th or -th qubits.
Pauli simplification
The measurement operations commute with the corrections in the following manner: : :, where . Such operation means that, when shifting the corrections at the end of the pattern, some dependencies between the measurements may occur. The operator is called signal shifting, whose action will be explained in the next paragraph. For particular angles, some simplifications, called Pauli simplifications, can be introduced: : :.Signal shifting
The action of the signal shifting operator can be explained through its rules of commutation: : :. The