NURBS on:
[Wikipedia]
[Google]
[Amazon]

 Non-uniform rational basis spline (NURBS) is a mathematical model using basis splines (B-splines) that is commonly used in
Non-uniform rational basis spline (NURBS) is a mathematical model using basis splines (B-splines) that is commonly used in
 Before computers, designs were drawn by hand on paper with various drafting tools.
Before computers, designs were drawn by hand on paper with various drafting tools.
 A NURBS curve is defined by its order, a set of weighted control points, and a knot vector. NURBS curves and surfaces are generalizations of both
A NURBS curve is defined by its order, a set of weighted control points, and a knot vector. NURBS curves and surfaces are generalizations of both
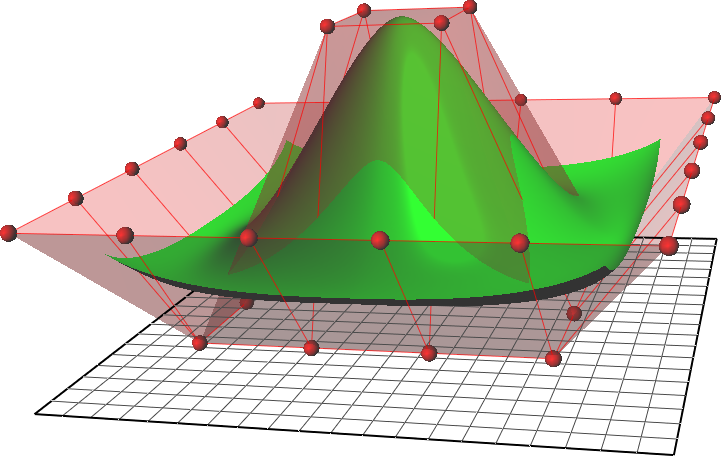
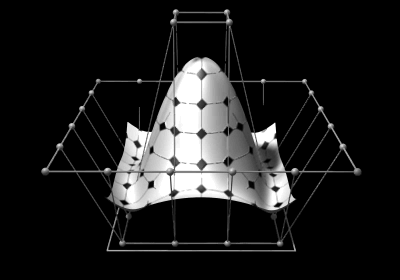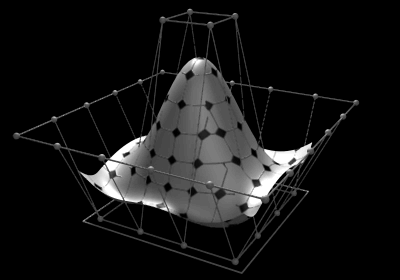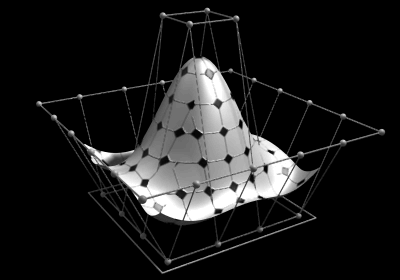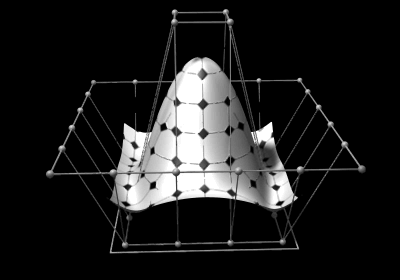 The control points determine the shape of the curve. Typically, each point of the curve is computed by taking a
The control points determine the shape of the curve. Typically, each point of the curve is computed by taking a
 :
rises linearly from zero to one on the interval where is non-zero, while falls from one to zero on the interval where is non-zero. As mentioned before, is a triangular function, nonzero over two knot spans rising from zero to one on the first, and falling to zero on the second knot span. Higher order basis functions are non-zero over corresponding more knot spans and have correspondingly higher degree. If is the parameter, and is the th knot, we can write the functions and as
:
and
:
The functions and are positive when the corresponding lower order basis functions are non-zero. By induction on n it follows that the basis functions are non-negative for all values of and . This makes the computation of the basis functions numerically stable.
Again by induction, it can be proved that the sum of the basis functions for a particular value of the parameter is unity. This is known as the partition of unity property of the basis functions.
The figures show the linear and the quadratic basis functions for the knots
One knot span is considerably shorter than the others. On that knot span, the peak in the quadratic basis function is more distinct, reaching almost one. Conversely, the adjoining basis functions fall to zero more quickly. In the geometrical interpretation, this means that the curve approaches the corresponding control point closely. In case of a double knot, the length of the knot span becomes zero and the peak reaches one exactly. The basis function is no longer differentiable at that point. The curve will have a sharp corner if the neighbour control points are not collinear.
:
rises linearly from zero to one on the interval where is non-zero, while falls from one to zero on the interval where is non-zero. As mentioned before, is a triangular function, nonzero over two knot spans rising from zero to one on the first, and falling to zero on the second knot span. Higher order basis functions are non-zero over corresponding more knot spans and have correspondingly higher degree. If is the parameter, and is the th knot, we can write the functions and as
:
and
:
The functions and are positive when the corresponding lower order basis functions are non-zero. By induction on n it follows that the basis functions are non-negative for all values of and . This makes the computation of the basis functions numerically stable.
Again by induction, it can be proved that the sum of the basis functions for a particular value of the parameter is unity. This is known as the partition of unity property of the basis functions.
The figures show the linear and the quadratic basis functions for the knots
One knot span is considerably shorter than the others. On that knot span, the peak in the quadratic basis function is more distinct, reaching almost one. Conversely, the adjoining basis functions fall to zero more quickly. In the geometrical interpretation, this means that the curve approaches the corresponding control point closely. In case of a double knot, the length of the knot span becomes zero and the peak reaches one exactly. The basis function is no longer differentiable at that point. The curve will have a sharp corner if the neighbour control points are not collinear.
 A number of transformations can be applied to a NURBS object. For instance, if some curve is defined using a certain degree and N control points, the same curve can be expressed using the same degree and N+1 control points. In the process a number of control points change position and a knot is inserted in the knot vector.
These manipulations are used extensively during interactive design. When adding a control point, the shape of the curve should stay the same, forming the starting point for further adjustments. A number of these operations are discussed below.
A number of transformations can be applied to a NURBS object. For instance, if some curve is defined using a certain degree and N control points, the same curve can be expressed using the same degree and N+1 control points. In the process a number of control points change position and a knot is inserted in the knot vector.
These manipulations are used extensively during interactive design. When adding a control point, the shape of the curve should stay the same, forming the starting point for further adjustments. A number of these operations are discussed below.
 Non-rational splines or
Non-rational splines or
Clear explanation of NURBS for non-experts
TinySpline: Opensource C-library with bindings for various languages
Computer-aided design Splines (mathematics) 3D computer graphics Interpolation Multivariate interpolation
 Non-uniform rational basis spline (NURBS) is a mathematical model using basis splines (B-splines) that is commonly used in
Non-uniform rational basis spline (NURBS) is a mathematical model using basis splines (B-splines) that is commonly used in computer graphics
Computer graphics deals with generating images with the aid of computers. Today, computer graphics is a core technology in digital photography, film, video games, cell phone and computer displays, and many specialized applications. A great de ...
for representing curves and surfaces
A surface, as the term is most generally used, is the outermost or uppermost layer of a physical object or space.
Surface or surfaces may also refer to:
Mathematics
*Surface (mathematics), a generalization of a plane which needs not be flat
* Sur ...
. It offers great flexibility and precision for handling both analytic (defined by common mathematical formula
In science, a formula is a concise way of expressing information symbolically, as in a mathematical formula or a ''chemical formula''. The informal use of the term ''formula'' in science refers to the general construct of a relationship betwe ...
e) and modeled shapes. It is a type of curve modeling, as opposed to polygonal modeling
In 3D computer graphics, polygonal modeling is an approach for modeling objects by representing or approximating their surfaces using polygon meshes. Polygonal modeling is well suited to scanline rendering and is therefore the method of choice f ...
or digital sculpting
Digital sculpting, also known as sculpt modeling or 3D sculpting, is the use of software that offers tools to push, pull, smooth, grab, pinch or otherwise manipulate a digital object as if it were made of a real-life substance such as clay.
Sculp ...
. NURBS curves are commonly used in computer-aided design
Computer-aided design (CAD) is the use of computers (or ) to aid in the creation, modification, analysis, or optimization of a design. This software is used to increase the productivity of the designer, improve the quality of design, improve co ...
(CAD), manufacturing
Manufacturing is the creation or production of goods with the help of equipment, labor, machines, tools, and chemical or biological processing or formulation. It is the essence of secondary sector of the economy. The term may refer to ...
(CAM), and engineering
Engineering is the use of scientific principles to design and build machines, structures, and other items, including bridges, tunnels, roads, vehicles, and buildings. The discipline of engineering encompasses a broad range of more speciali ...
(CAE). They are part of numerous industry-wide standards, such as IGES
The Initial Graphics Exchange Specification (IGES) is a vendor-neutral file format that allows the digital exchange of information among computer-aided design (CAD) systems. It's an ASCII-based textual format.
The official title of IGES is ''Dig ...
, STEP, ACIS, and PHIGS
PHIGS (Programmer's Hierarchical Interactive Graphics System) is an application programming interface (API) standard for rendering 3D computer graphics, considered to be the 3D graphics standard for the 1980s through the early 1990s. Subsequently, ...
. Tools for creating and editing NURBS surfaces are found in various 3D graphics
3D computer graphics, or “3D graphics,” sometimes called CGI, 3D-CGI or three-dimensional computer graphics are graphics that use a three-dimensional representation of geometric data (often Cartesian) that is stored in the computer for th ...
and animation
Animation is a method by which still figures are manipulated to appear as moving images. In traditional animation, images are drawn or painted by hand on transparent celluloid sheets to be photographed and exhibited on film. Today, most ani ...
software packages.
They can be efficiently handled by computer programs yet allow for easy human interaction. NURBS surfaces are functions of two parameter
A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when ...
s mapping to a surface in three-dimensional space
Three-dimensional space (also: 3D space, 3-space or, rarely, tri-dimensional space) is a geometric setting in which three values (called ''parameters'') are required to determine the position of an element (i.e., point). This is the informa ...
. The shape of the surface is determined by control points. In a compact form, NURBS surfaces can represent simple geometrical shapes. For complex organic shapes, T-splines and subdivision surfaces
In the field of 3D computer graphics, a subdivision surface (commonly shortened to SubD surface) is a curved surface represented by the specification of a coarser polygon mesh and produced by a recursive algorithmic method. The curved surface, ...
are more suitable because they halve the number of control points in comparison with the NURBS surfaces.
In general, editing NURBS curves and surfaces is intuitive and predictable. Control points are always either connected directly to the curve or surface, or else act as if they were connected by a rubber band. Depending on the type of user interface, the editing of NURBS curves and surfaces can be via their control points (similar to Bézier curve
A Bézier curve ( ) is a parametric curve used in computer graphics and related fields. A set of discrete "control points" defines a smooth, continuous curve by means of a formula. Usually the curve is intended to approximate a real-world shape ...
s) or via higher level tools such as ''spline modeling'' and ''hierarchical editing''.
Historical background
 Before computers, designs were drawn by hand on paper with various drafting tools.
Before computers, designs were drawn by hand on paper with various drafting tools. Ruler
A ruler, sometimes called a rule, line gauge, or scale, is a device used in geometry and technical drawing, as well as the engineering and construction industries, to measure distances or draw straight lines.
Variants
Rulers have long ...
s were used for straight lines, compasses for circles, and protractor
A protractor is a measuring instrument, typically made of transparent plastic or glass, for measuring angles.
Some protractors are simple half-discs or full circles. More advanced protractors, such as the bevel protractor, have one or two sw ...
s for angles. But many shapes, such as the freeform curve
Freeform surface modelling is a technique for engineering freeform surfaces with a CAD or CAID system.
The technology has encompassed two main fields. Either creating aesthetic surfaces (class A surfaces) that also perform a function; for exam ...
of a ship's bow, could not be drawn with these tools. Although such curves could be drawn freehand at the drafting board, shipbuilders often needed a life-size version which could not be done by hand. Such large drawings were done with the help of flexible strips of wood, called splines. The splines were held in place at a number of predetermined points, called "ducks"; between the ducks, the elasticity of the spline material caused the strip to take the shape that minimized the energy of bending, thus creating the smoothest possible shape that fit the constraints. The shape could be adjusted by moving the ducks.
In 1946, mathematicians started studying the spline shape, and derived the piecewise polynomial
In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An exampl ...
formula known as the spline curve
In mathematics, a spline is a special function defined piecewise by polynomials.
In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low degree poly ...
or spline function. I. J. Schoenberg gave the spline function its name after its resemblance to the mechanical spline used by draftsmen.
As computers were introduced into the design process, the physical properties of such splines were investigated so that they could be modelled with mathematical precision and reproduced where needed. Pioneering work was done in France
France (), officially the French Republic ( ), is a country primarily located in Western Europe. It also comprises of Overseas France, overseas regions and territories in the Americas and the Atlantic Ocean, Atlantic, Pacific Ocean, Pac ...
by Renault
Groupe Renault ( , , , also known as the Renault Group in English; legally Renault S.A.) is a French multinational automobile manufacturer established in 1899. The company produces a range of cars and vans, and in the past has manufactured ...
engineer Pierre Bézier
Pierre Étienne Bézier (1 September 1910 – 25 November 1999; ) was a French engineer and one of the founders of the fields of solid, geometric and physical modelling as well as in the field of representing curves, especially in computer-ai ...
, and Citroën
Citroën () is a French automobile brand. The "Automobiles Citroën" manufacturing company was founded in March 1919 by André Citroën. Citroën is owned by Stellantis since 2021 and previously was part of the PSA Group after Peugeot acquired 8 ...
's physicist and mathematician Paul de Casteljau
Paul de Casteljau (19 November 1930 – 24 March 2022) was a French physicist and mathematician. In 1959, while working at Citroën, he developed an algorithm for evaluating calculations on a certain family of curves, which would later be formali ...
. They worked nearly parallel to each other, but because Bézier published the results of his work, Bézier curves were named after him, while de Casteljau's name is only associated with related algorithms.
At first NURBS were only used in the proprietary CAD
Computer-aided design (CAD) is the use of computers (or ) to aid in the creation, modification, analysis, or optimization of a design. This software is used to increase the productivity of the designer, improve the quality of design, improve c ...
packages of car companies. Later they became part of standard computer graphics packages.
Real-time, interactive rendering of NURBS curves and surfaces was first made commercially available on Silicon Graphics
Silicon Graphics, Inc. (stylized as SiliconGraphics before 1999, later rebranded SGI, historically known as Silicon Graphics Computer Systems or SGCS) was an American high-performance computing manufacturer, producing computer hardware and soft ...
workstations in 1989. In 1993, the first interactive NURBS modeller for PCs, called NöRBS, was developed by CAS Berlin, a small startup company cooperating with the Technical University of Berlin
The Technical University of Berlin (official name both in English and german: link=no, Technische Universität Berlin, also known as TU Berlin and Berlin Institute of Technology) is a public research university located in Berlin, Germany. It was ...
.
Continuity
A surface under construction, e.g. the hull of a motor yacht, is usually composed of several NURBS surfaces known as NURBS patches (or just ''patches''). These surface patches should be fitted together in such a way that the boundaries are invisible. This is mathematically expressed by the concept of geometric continuity. Higher-level tools exist that benefit from the ability of NURBS to create and establish geometric continuity of different levels: * Positional continuity (G0) holds whenever the end positions of two curves or surfaces coincide. The curves or surfaces may still meet at an angle, giving rise to a sharp corner or edge and causing broken highlights. * Tangential continuity (G¹) requires the end vectors of the curves or surfaces to be parallel and pointing the same way, ruling out sharp edges. Because highlights falling on a tangentially continuous edge are always continuous and thus look natural, this level of continuity can often be sufficient. * Curvature continuity (G²) further requires the end vectors to be of the same length and rate of length change. Highlights falling on a curvature-continuous edge do not display any change, causing the two surfaces to appear as one. This can be visually recognized as "perfectly smooth". This level of continuity is very useful in the creation of models that require many bi-cubic patches composing one continuous surface. Geometric continuity mainly refers to the shape of the resulting surface; since NURBS surfaces are functions, it is also possible to discuss the derivatives of the surface with respect to the parameters. This is known asparametric continuity
In mathematical analysis, the smoothness of a function (mathematics), function is a property measured by the number of Continuous function, continuous Derivative (mathematics), derivatives it has over some domain, called ''differentiability cl ...
. Parametric continuity of a given degree implies geometric continuity of that degree.
First- and second-level parametric continuity (C0 and C¹) are for practical purposes identical to positional and tangential (G0 and G¹) continuity. Third-level parametric continuity (C²), however, differs from curvature continuity in that its parameterization is also continuous. In practice, C² continuity is easier to achieve if uniform B-splines are used.
The definition of C''n'' continuity requires that the ''n''th derivative of adjacent curves/surfaces () are equal at a joint. Note that the (partial) derivatives of curves and surfaces are vectors that have a direction and a magnitude; both should be equal.
Highlights and reflections can reveal the perfect smoothing, which is otherwise practically impossible to achieve without NURBS surfaces that have at least G² continuity. This same principle is used as one of the surface evaluation methods whereby a ray-traced or reflection-mapped image of a surface with white stripes reflecting on it will show even the smallest deviations on a surface or set of surfaces. This method is derived from car prototyping wherein surface quality is inspected by checking the quality of reflections of a neon-light ceiling on the car surface. This method is also known as "Zebra analysis".
Technical specifications
B-spline
In the mathematical subfield of numerical analysis, a B-spline or basis spline is a spline function that has minimal support with respect to a given degree, smoothness, and domain partition. Any spline function of given degree can be expresse ...
s and Bézier curve
A Bézier curve ( ) is a parametric curve used in computer graphics and related fields. A set of discrete "control points" defines a smooth, continuous curve by means of a formula. Usually the curve is intended to approximate a real-world shape ...
s and surfaces, the primary difference being the weighting of the control points, which makes NURBS curves ''rational''. (''Non-rational'', aka ''simple'', B-splines are a special case/subset of rational B-splines, where each control point is a regular non-homogenous coordinate o 'w'
O, or o, is the fifteenth letter and the fourth vowel letter in the Latin alphabet, used in the modern English alphabet, the alphabets of other western European languages and others worldwide. Its name in English is ''o'' (pronounced ), pl ...
rather than a homogeneous coordinate
In mathematics, homogeneous coordinates or projective coordinates, introduced by August Ferdinand Möbius in his 1827 work , are a system of coordinates used in projective geometry, just as Cartesian coordinates are used in Euclidean geometr ...
. That is equivalent to having weight "1" at each control point; ''Rational'' B-splines use the 'w' of each control point as a weight.)
By using a two-dimensional grid of control points, NURBS surfaces including planar patches and sections of spheres can be created. These are parametrized with two variables (typically called ''s'' and ''t'' or ''u'' and ''v''). This can be extended to arbitrary dimensions to create NURBS mapping .
NURBS curves and surfaces are useful for a number of reasons:
* The set of NURBS for a given order is invariant under affine
Affine may describe any of various topics concerned with connections or affinities.
It may refer to:
* Affine, a relative by marriage in law and anthropology
* Affine cipher, a special case of the more general substitution cipher
* Affine comb ...
transformations: operations like rotations and translations can be applied to NURBS curves and surfaces by applying them to their control points.
* They offer one common mathematical form for both standard analytical shapes (e.g., conics) and free-form shapes.
* They provide the flexibility to design a large variety of shapes.
* They reduce the memory consumption when storing shapes (compared to simpler methods).
* They can be evaluated reasonably quickly by numerically stable and accurate algorithm
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific problems or to perform a computation. Algorithms are used as specifications for performing ...
s.
Here, NURBS is mostly discussed in one dimension (curves); it can be generalized to two (surfaces) or even more dimensions.
Order
The ''order'' of a NURBS curve defines the number of nearby control points that influence any given point on the curve. The curve is represented mathematically by a polynomial of degree one less than the order of the curve. Hence, second-order curves (which are represented by linear polynomials) are called linear curves, third-order curves are called quadratic curves, and fourth-order curves are called cubic curves. The number of control points must be greater than or equal to the order of the curve. In practice, cubic curves are the ones most commonly used. Fifth- and sixth-order curves are sometimes useful, especially for obtaining continuous higher order derivatives, but curves of higher orders are practically never used because they lead to internal numerical problems and tend to require disproportionately large calculation times.Control points
 The control points determine the shape of the curve. Typically, each point of the curve is computed by taking a
The control points determine the shape of the curve. Typically, each point of the curve is computed by taking a weighted
A weight function is a mathematical device used when performing a sum, integral, or average to give some elements more "weight" or influence on the result than other elements in the same set. The result of this application of a weight function is ...
sum of a number of control points. The weight of each point varies according to the governing parameter. For a curve of degree d, the weight of any control point is only nonzero in d+1 intervals of the parameter space. Within those intervals, the weight changes according to a polynomial function (''basis functions'') of degree d. At the boundaries of the intervals, the basis functions go smoothly to zero, the smoothness being determined by the degree of the polynomial.
As an example, the basis function of degree one is a triangle function. It rises from zero to one, then falls to zero again. While it rises, the basis function of the previous control point falls. In that way, the curve interpolates between the two points, and the resulting curve is a polygon, which is continuous
Continuity or continuous may refer to:
Mathematics
* Continuity (mathematics), the opposing concept to discreteness; common examples include
** Continuous probability distribution or random variable in probability and statistics
** Continuous g ...
, but not differentiable
In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non-vertical tangent line at each interior point in its ...
at the interval boundaries, or knots. Higher degree polynomials have correspondingly more continuous derivatives. Note that within the interval the polynomial nature of the basis functions and the linearity of the construction make the curve perfectly smooth, so it is only at the knots that discontinuity can arise.
In many applications the fact that a single control point only influences those intervals where it is active is a highly desirable property, known as local support. In modeling, it allows the changing of one part of a surface while keeping other parts unchanged.
Adding more control points allows better approximation to a given curve, although only a certain class of curves can be represented exactly with a finite number of control points. NURBS curves also feature a scalar weight for each control point. This allows for more control over the shape of the curve without unduly raising the number of control points. In particular, it adds conic sections like circles and ellipses to the set of curves that can be represented exactly. The term ''rational'' in NURBS refers to these weights.
The control points can have any dimensionality
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coordin ...
. One-dimensional points just define a scalar function of the parameter. These are typically used in image processing programs to tune the brightness and color curves. Three-dimensional control points are used abundantly in 3D modeling, where they are used in the everyday meaning of the word 'point', a location in 3D space.
Multi-dimensional points might be used to control sets of time-driven values, e.g. the different positional and rotational settings of a robot arm. NURBS surfaces are just an application of this. Each control 'point' is actually a full vector of control points, defining a curve. These curves share their degree and the number of control points, and span one dimension of the parameter space. By interpolating these control vectors over the other dimension of the parameter space, a continuous set of curves is obtained, defining the surface.
Knot vector
The knot vector is a sequence of parameter values that determines where and how the control points affect the NURBS curve. The number of knots is always equal to the number of control points plus curve degree plus one (i.e. number of control points plus curve order). The knot vector divides the parametric space in the intervals mentioned before, usually referred to as ''knot spans''. Each time the parameter value enters a new knot span, a new control point becomes active, while an old control point is discarded. It follows that the values in the knot vector should be in nondecreasing order, so (0, 0, 1, 2, 3, 3) is valid while (0, 0, 2, 1, 3, 3) is not. Consecutive knots can have the same value. This then defines a knot span of zero length, which implies that two control points are activated at the same time (and of course two control points become deactivated). This has impact on continuity of the resulting curve or its higher derivatives; for instance, it allows the creation of corners in an otherwise smooth NURBS curve. A number of coinciding knots is sometimes referred to as a knot with a certain multiplicity. Knots with multiplicity two or three are known as double or triple knots. The multiplicity of a knot is limited to the degree of the curve; since a higher multiplicity would split the curve into disjoint parts and it would leave control points unused. For first-degree NURBS, each knot is paired with a control point. The knot vector usually starts with a knot that has multiplicity equal to the order. This makes sense, since this activates the control points that have influence on the first knot span. Similarly, the knot vector usually ends with a knot of that multiplicity. Curves with such knot vectors start and end in a control point. The values of the knots control the mapping between the input parameter and the corresponding NURBS value. For example, if a NURBS describes a path through space over time, the knots control the time that the function proceeds past the control points. For the purposes of representing shapes, however, only the ratios of the difference between the knot values matter; in that case, the knot vectors (0, 0, 1, 2, 3, 3) and (0, 0, 2, 4, 6, 6) produce the same curve. The positions of the knot values influences the mapping of parameter space to curve space. Rendering a NURBS curve is usually done by stepping with a fixed stride through the parameter range. By changing the knot span lengths, more sample points can be used in regions where the curvature is high. Another use is in situations where the parameter value has some physical significance, for instance if the parameter is time and the curve describes the motion of a robot arm. The knot span lengths then translate into velocity and acceleration, which are essential to get right to prevent damage to the robot arm or its environment. This flexibility in the mapping is what the phrase ''non uniform'' in NURBS refers to. Necessary only for internal calculations, knots are usually not helpful to the users of modeling software. Therefore, many modeling applications do not make the knots editable or even visible. It's usually possible to establish reasonable knot vectors by looking at the variation in the control points. More recent versions of NURBS software (e.g.,Autodesk Maya
Autodesk Maya, commonly shortened to just Maya ( ), is a 3D computer graphics application that runs on Windows, macOS and Linux, originally developed by Alias and currently owned and developed by Autodesk. It is used to create assets for interact ...
and Rhinoceros 3D) allow for interactive editing of knot positions, but this is significantly less intuitive than the editing of control points.
Construction of the basis functions
The B-spline basis functions used in the construction of NURBS curves are usually denoted as , in which corresponds to the th control point, and corresponds with the degree of the basis function. The parameter dependence is frequently left out, so we can write . The definition of these basis functions is recursive in . The degree-0 functions arepiecewise
In mathematics, a piecewise-defined function (also called a piecewise function, a hybrid function, or definition by cases) is a function defined by multiple sub-functions, where each sub-function applies to a different interval in the domain. P ...
constant function
In mathematics, a constant function is a function whose (output) value is the same for every input value. For example, the function is a constant function because the value of is 4 regardless of the input value (see image).
Basic propertie ...
s. They are one on the corresponding knot span and zero everywhere else.
Effectively, is a linear interpolation of and . The latter two functions are non-zero for
knot spans, overlapping for knot spans. The function is computed as
General form of a NURBS curve
Using the definitions of the basis functions from the previous paragraph, a NURBS curve takes the following form: : In this, is the number of control points and are the corresponding weights. The denominator is a normalizing factor that evaluates to one if all weights are one. This can be seen from the partition of unity property of the basis functions. It is customary to write this as : in which the functions : are known as the ''rational basis functions''.General form of a NURBS surface
A NURBS surface is obtained as thetensor product
In mathematics, the tensor product V \otimes W of two vector spaces and (over the same field) is a vector space to which is associated a bilinear map V\times W \to V\otimes W that maps a pair (v,w),\ v\in V, w\in W to an element of V \otime ...
of two NURBS curves, thus using two independent parameters and (with indices and respectively):
:
with
:
as rational basis functions.
Manipulating NURBS objects
 A number of transformations can be applied to a NURBS object. For instance, if some curve is defined using a certain degree and N control points, the same curve can be expressed using the same degree and N+1 control points. In the process a number of control points change position and a knot is inserted in the knot vector.
These manipulations are used extensively during interactive design. When adding a control point, the shape of the curve should stay the same, forming the starting point for further adjustments. A number of these operations are discussed below.
A number of transformations can be applied to a NURBS object. For instance, if some curve is defined using a certain degree and N control points, the same curve can be expressed using the same degree and N+1 control points. In the process a number of control points change position and a knot is inserted in the knot vector.
These manipulations are used extensively during interactive design. When adding a control point, the shape of the curve should stay the same, forming the starting point for further adjustments. A number of these operations are discussed below.
Knot insertion
As the term suggests, knot insertion inserts a knot into the knot vector. If the degree of the curve is , then control points are replaced by new ones. The shape of the curve stays the same. A knot can be inserted multiple times, up to the maximum multiplicity of the knot. This is sometimes referred to as knot refinement and can be achieved by an algorithm that is more efficient than repeated knot insertion.Knot removal
Knot removal is the reverse of knot insertion. Its purpose is to remove knots and the associated control points in order to get a more compact representation. Obviously, this is not always possible while retaining the exact shape of the curve. In practice, a tolerance in the accuracy is used to determine whether a knot can be removed. The process is used to clean up after an interactive session in which control points may have been added manually, or after importing a curve from a different representation, where a straightforward conversion process leads to redundant control points.Degree elevation
A NURBS curve of a particular degree can always be represented by a NURBS curve of higher degree. This is frequently used when combining separate NURBS curves, e.g., when creating a NURBS surface interpolating between a set of NURBS curves or when unifying adjacent curves. In the process, the different curves should be brought to the same degree, usually the maximum degree of the set of curves. The process is known as degree elevation.Curvature
The most important property indifferential geometry
Differential geometry is a mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of differential calculus, integral calculus, linear algebra and mult ...
is the curvature
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.
For curves, the can ...
. It describes the local properties (edges, corners, etc.) and relations between the first and second derivative, and thus, the precise curve shape. Having determined the derivatives it is easy to compute or approximated as the arclength from the second derivative . The direct computation of the curvature with these equations is the big advantage of parameterized curves against their polygonal representations.
Example: a circle
Bézier curve
A Bézier curve ( ) is a parametric curve used in computer graphics and related fields. A set of discrete "control points" defines a smooth, continuous curve by means of a formula. Usually the curve is intended to approximate a real-world shape ...
s may approximate a circle, but they cannot represent it exactly. Rational splines can represent any conic section, including the circle, exactly. This representation is not unique, but one possibility appears below:
The order is three, since a circle is a quadratic curve and the spline's order is one more than the degree of its piecewise polynomial segments. The knot vector is . The circle is composed of four quarter circles, tied together with double knots. Although double knots in a third order NURBS curve would normally result in loss of continuity in the first derivative, the control points are positioned in such a way that the first derivative is continuous. In fact, the curve is infinitely differentiable everywhere, as it must be if it exactly represents a circle.
The curve represents a circle exactly, but it is not exactly parametrized in the circle's arc length. This means, for example, that the point at does not lie at (except for the start, middle and end point of each quarter circle, since the representation is symmetrical). This would be impossible, since the ''x'' coordinate of the circle would provide an exact rational polynomial expression for , which is impossible. The circle does make one full revolution as its parameter goes from 0 to , but this is only because the knot vector was arbitrarily chosen as multiples of .
See also
* Spline *Bézier surface
Bézier surfaces are a species of mathematical spline used in computer graphics, computer-aided design, and finite element modeling.
As with Bézier curves, a Bézier surface is defined by a set of control points. Similar to interpolation in man ...
* de Boor's algorithm In the mathematical subfield of numerical analysis de Boor's algorithmC. de Boor 971 "Subroutine package for calculating with B-splines", Techn.Rep. LA-4728-MS, Los Alamos Sci.Lab, Los Alamos NM; p. 109, 121. is a polynomial-time and numerically s ...
* Triangle mesh
* Point cloud
Point or points may refer to:
Places
* Point, Lewis, a peninsula in the Outer Hebrides, Scotland
* Point, Texas, a city in Rains County, Texas, United States
* Point, the NE tip and a ferry terminal of Lismore, Inner Hebrides, Scotland
* Poin ...
* Rational motion
* Isogeometric analysis Isogeometric analysis is a computational approach that offers the possibility of integrating finite element analysis (FEA) into conventional NURBS-based CAD design tools. Currently, it is necessary to convert data between CAD and FEA packages to an ...
References
External links
Clear explanation of NURBS for non-experts
TinySpline: Opensource C-library with bindings for various languages
Computer-aided design Splines (mathematics) 3D computer graphics Interpolation Multivariate interpolation