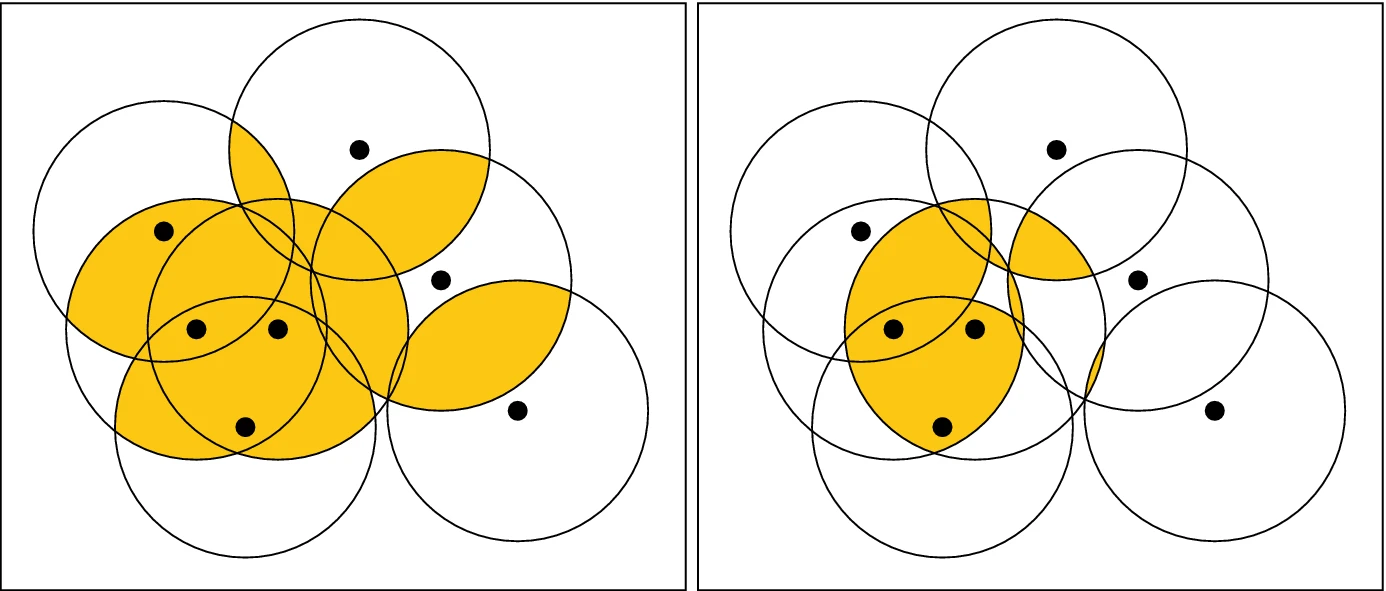The multicover bifiltration is a two-parameter sequence of nested

topological spaces In mathematics, a topological space is, roughly speaking, a geometrical space in which closeness is defined but cannot necessarily be measured by a numeric distance. More specifically, a topological space is a set whose elements are called point ...

derived from the covering of a

finite set In mathematics, particularly set theory, a finite set is a set that has a finite number of elements. Informally, a finite set is a set which one could in principle count and finish counting. For example, is a finite set with five elements. Th ...

in a

metric space In mathematics, a metric space is a Set (mathematics), set together with a notion of ''distance'' between its Element (mathematics), elements, usually called point (geometry), points. The distance is measured by a function (mathematics), functi ...

by growing metric balls. It is a multidimensional extension of the

offset filtration The offset filtration (also called the "union-of-balls" or "union-of-disks" filtration) is a growing sequence of metric balls used to detect the size and scale of topological features of a data set. The offset filtration commonly arises in persis ...

that captures density information about the underlying data set by filtering the points of the offsets at each index according to how many balls cover each point. The multicover bifiltration has been an object of study within multidimensional

persistent homology In topological data analysis, persistent homology is a method for computing topological features of a space at different spatial resolutions. More persistent features are detected over a wide range of spatial scales and are deemed more likely to ...

and

topological data analysis In applied mathematics, topological data analysis (TDA) is an approach to the analysis of datasets using techniques from topology. Extraction of information from datasets that are high-dimensional, incomplete and noisy is generally challenging. TDA ...

Definition

Following the notation of Corbet et al. (2022), given a finite set

A\subset \mathbb R^d

, the multicover bifiltration on

A

is a two-parameter filtration indexed by

\mathbb R \times \mathbb N^

defined index-wise as

\operatorname_ := \

, where

\mathbb N

denotes the non-negative integers.{{Cite journal , last1=Corbet , first1=René , last2=Kerber , first2=Michael , last3=Lesnick , first3=Michael , last4=Osang , first4=Georg , date=2023-02-20 , title=Computing the Multicover Bifiltration , journal=Discrete & Computational Geometry , volume=70 , issue=2 , pages=376–405 , language=en , doi=10.1007/s00454-022-00476-8 , pmid=37581017 , pmc=10423148 , issn=0179-5376, arxiv=2103.07823 Note that when

k=1

is fixed we recover the

Offset Filtration The offset filtration (also called the "union-of-balls" or "union-of-disks" filtration) is a growing sequence of metric balls used to detect the size and scale of topological features of a data set. The offset filtration commonly arises in persis ...

Properties

The multicover bifiltration admits a topologically equivalent polytopal model of polynomial size, called the "

rhomboid Traditionally, in two-dimensional geometry, a rhomboid is a parallelogram in which adjacent sides are of unequal lengths and angles are non-right angled. The terms "rhomboid" and "parallelogram" are often erroneously conflated with each oth ...

bifiltration." The rhomboid bifiltration is an extension of the rhomboid

tiling Tiling may refer to: *The physical act of laying tiles *Tessellations Computing *The compiler optimization of loop tiling *Tiled rendering, the process of subdividing an image by regular grid *Tiling window manager People *Heinrich Sylvester The ...

introduced by Edelsbrunner and Osang in 2021 for computing the

of the multicover bifiltration along one axis of the indexing set. The rhomboid bifiltration on a set of

n

points in a

Euclidean space Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...

can be computed in polynomial time. Rhomboid_Tiling

The multicover bifiltration is also topologically equivalent to a multicover nerve construction due to Sheehy called the subdivision-Čech bifiltration, which considers the

barycentric subdivision In mathematics, the barycentric subdivision is a standard way to subdivide a given simplex into smaller ones. Its extension to simplicial complexes is a canonical method to refining them. Therefore, the barycentric subdivision is an important tool ...

on the nerve of the offsets.D. R. Sheehy, �
A multicover nerve for geometric inference
” in ''CCCG: Canadian conference in computational geometry'', 2012. In particular, the subdivision-Čech and multicover bifiltrations are weakly equivalent, and hence have

isomorphic In mathematics, an isomorphism is a structure-preserving mapping or morphism between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between the ...

homology modules in all dimensions. However, the subdivision-Čech bifiltration has an exponential number of simplices in the size of the data set, and hence is not amenable to efficient direct computations.

References

Computational geometry Topology Geometry