Morton order on:
[Wikipedia]
[Google]
[Amazon]
 In
In
 The figure below shows the Z-values for the two dimensional case with integer coordinates 0 ≤ ''x'' ≤ 7, 0 ≤ ''y'' ≤ 7 (shown both in decimal and binary). Interleaving the binary coordinate values (starting to the right with the ''x''-bit (in blue) and alternating to the left with the ''y''-bit (in red)) yields the binary ''z''-values (tilted by 45° as shown). Connecting the ''z''-values in their numerical order produces the recursively Z-shaped curve. Two-dimensional Z-values are also known as quadkey values.
The figure below shows the Z-values for the two dimensional case with integer coordinates 0 ≤ ''x'' ≤ 7, 0 ≤ ''y'' ≤ 7 (shown both in decimal and binary). Interleaving the binary coordinate values (starting to the right with the ''x''-bit (in blue) and alternating to the left with the ''y''-bit (in red)) yields the binary ''z''-values (tilted by 45° as shown). Connecting the ''z''-values in their numerical order produces the recursively Z-shaped curve. Two-dimensional Z-values are also known as quadkey values.
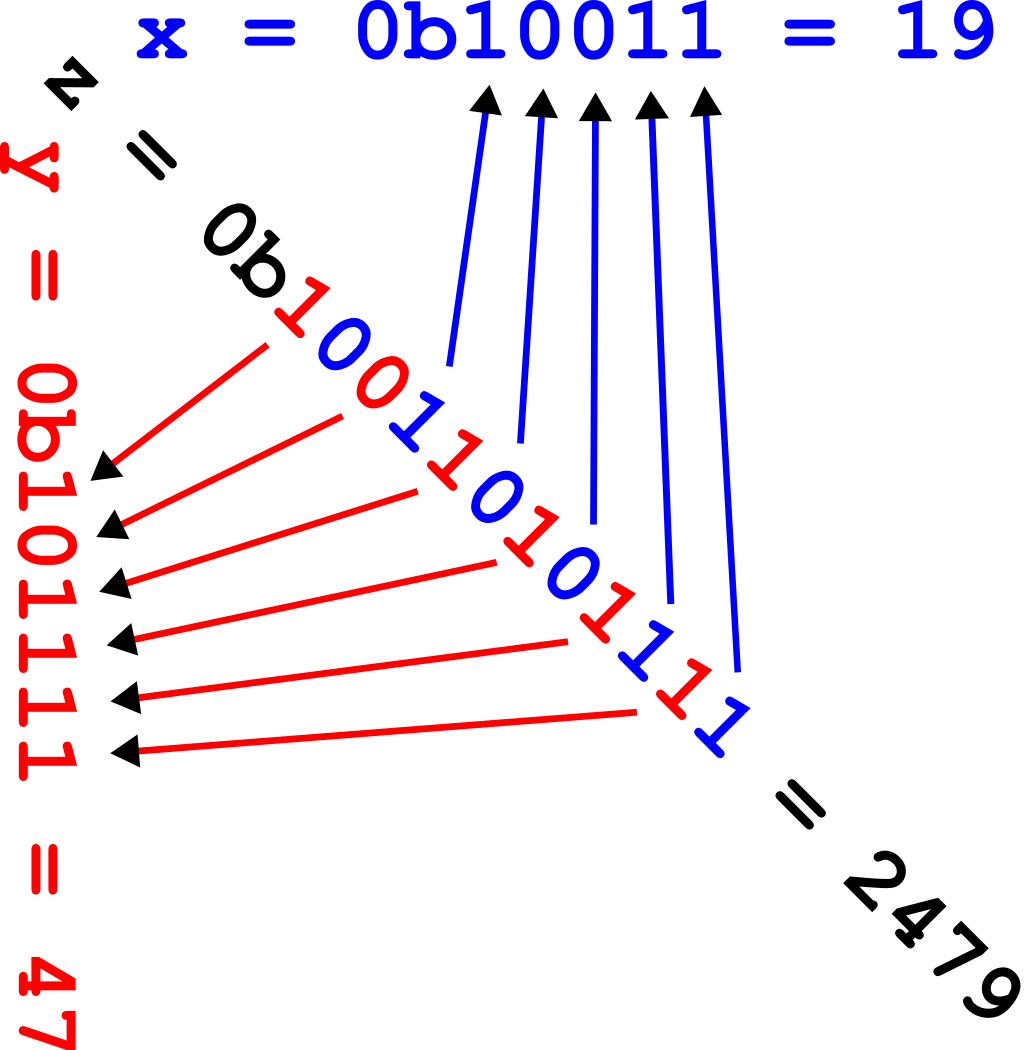
 The Z-values of the ''x'' coordinates are described as binary numbers from the
The Z-values of the ''x'' coordinates are described as binary numbers from the
def cmp_zorder(lhs, rhs) -> bool:
"""Compare z-ordering."""
# Assume lhs and rhs array-like objects of indices.
assert len(lhs) len(rhs)
# Will contain the most significant dimension.
msd = 0
# Loop over the other dimensions.
for dim in range(1, len(lhs)):
# Check if the current dimension is more significant
# by comparing the most significant bits.
if less_msb(lhs sd^ rhs sd lhs im^ rhs im:
msd = dim
return lhs sd< rhs sd
One way to determine whether the most significant bit is smaller is to compare the floor of the base-2 logarithm of each point. It turns out the following operation is equivalent, and only requires exclusive or operations:
def less_msb(x: int, y: int) -> bool:
return x < y and x < (x ^ y)
It is also possible to compare floating point numbers using the same technique. The
 In this example, the range being queried (''x'' = 2, ..., 3, ''y'' = 2, ..., 6) is indicated by the dotted rectangle. Its highest Z-value (MAX) is 45. In this example, the value ''F'' = 19 is encountered when searching a data structure in increasing Z-value direction, so we would have to search in the interval between ''F'' and MAX (hatched area). To speed up the search, one would calculate the next Z-value which is in the search range, called BIGMIN (36 in the example) and only search in the interval between BIGMIN and MAX (bold values), thus skipping most of the hatched area. Searching in decreasing direction is analogous with LITMAX which is the highest Z-value in the query range lower than ''F''. The BIGMIN problem has first been stated and its solution shown in Tropf and Herzog. This solution is also used in
In this example, the range being queried (''x'' = 2, ..., 3, ''y'' = 2, ..., 6) is indicated by the dotted rectangle. Its highest Z-value (MAX) is 45. In this example, the value ''F'' = 19 is encountered when searching a data structure in increasing Z-value direction, so we would have to search in the interval between ''F'' and MAX (hatched area). To speed up the search, one would calculate the next Z-value which is in the search range, called BIGMIN (36 in the example) and only search in the interval between BIGMIN and MAX (bold values), thus skipping most of the hatched area. Searching in decreasing direction is analogous with LITMAX which is the highest Z-value in the query range lower than ''F''. The BIGMIN problem has first been stated and its solution shown in Tropf and Herzog. This solution is also used in

STANN: A library for approximate nearest neighbor search, using Z-order curve
Sean Eron Anderson, Stanford University Fractal curves Database algorithms Geometric data structures Database index techniques Linear algebra
mathematical analysis
Analysis is the branch of mathematics dealing with continuous functions, limit (mathematics), limits, and related theories, such as Derivative, differentiation, Integral, integration, measure (mathematics), measure, infinite sequences, series (m ...
and computer science
Computer science is the study of computation, automation, and information. Computer science spans theoretical disciplines (such as algorithms, theory of computation, information theory, and automation) to Applied science, practical discipli ...
, functions which are Z-order, Lebesgue curve, Morton space-filling curve, Morton order or Morton code map multidimensional data to one dimension while preserving locality of the data points. It is named in France after Henri Lebesgue
Henri Léon Lebesgue (; June 28, 1875 – July 26, 1941) was a French mathematician known for his theory of integration, which was a generalization of the 17th-century concept of integration—summing the area between an axis and the curve of ...
, who studied it in 1904, and named in US after Guy Macdonald Morton, who first applied the order to file sequencing in 1966. The z-value of a point in multidimensions is simply calculated by interleaving the binary
Binary may refer to:
Science and technology Mathematics
* Binary number, a representation of numbers using only two digits (0 and 1)
* Binary function, a function that takes two arguments
* Binary operation, a mathematical operation that t ...
representations of its coordinate values. Once the data are sorted into this ordering, any one-dimensional data structure can be used such as binary search tree
In computer science, a binary search tree (BST), also called an ordered or sorted binary tree, is a rooted binary tree data structure with the key of each internal node being greater than all the keys in the respective node's left subtree and ...
s, B-tree
In computer science, a B-tree is a self-balancing tree data structure that maintains sorted data and allows searches, sequential access, insertions, and deletions in logarithmic time. The B-tree generalizes the binary search tree, allowing for n ...
s, skip list
In computer science, a skip list (or skiplist) is a probabilistic data structure that allows \mathcal(\log n) average complexity for search as well as \mathcal(\log n) average complexity for insertion within an ordered sequence of n elements. T ...
s or (with low significant bits truncated) hash table
In computing, a hash table, also known as hash map, is a data structure that implements an associative array or dictionary. It is an abstract data type that maps keys to values. A hash table uses a hash function to compute an ''index'', als ...
s. The resulting ordering can equivalently be described as the order one would get from a depth-first
Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible alon ...
traversal of a quadtree
A quadtree is a tree data structure in which each internal node has exactly four children. Quadtrees are the two-dimensional analog of octrees and are most often used to partition a two-dimensional space by recursively subdividing it into four ...
or octree
An octree is a tree data structure in which each internal node has exactly eight children. Octrees are most often used to partition a three-dimensional space by recursively subdividing it into eight octants. Octrees are the three-dimensional ana ...
.
Coordinate values
 The figure below shows the Z-values for the two dimensional case with integer coordinates 0 ≤ ''x'' ≤ 7, 0 ≤ ''y'' ≤ 7 (shown both in decimal and binary). Interleaving the binary coordinate values (starting to the right with the ''x''-bit (in blue) and alternating to the left with the ''y''-bit (in red)) yields the binary ''z''-values (tilted by 45° as shown). Connecting the ''z''-values in their numerical order produces the recursively Z-shaped curve. Two-dimensional Z-values are also known as quadkey values.
The figure below shows the Z-values for the two dimensional case with integer coordinates 0 ≤ ''x'' ≤ 7, 0 ≤ ''y'' ≤ 7 (shown both in decimal and binary). Interleaving the binary coordinate values (starting to the right with the ''x''-bit (in blue) and alternating to the left with the ''y''-bit (in red)) yields the binary ''z''-values (tilted by 45° as shown). Connecting the ''z''-values in their numerical order produces the recursively Z-shaped curve. Two-dimensional Z-values are also known as quadkey values.
Moser–de Bruijn sequence
In number theory, the Moser–de Bruijn sequence is an integer sequence named after Leo Moser and Nicolaas Govert de Bruijn, consisting of the sums of distinct powers of 4, or equivalently the numbers whose binary representations are nonzero o ...
, having nonzero bits only in their even positions:
x[] =
The sum and difference of two ''x'' values are calculated by using bitwise operations:
x[i+j] = ((x[i] , 0b10101010) + x[j]) & 0b01010101
x[i−j] = ((x[i] & 0b01010101) − x[j]) & 0b01010101 if i ≥ j
This property can be used to offset a Z-value, for example in two dimensions the coordinates to the top (decreasing y), bottom (increasing y), left (decreasing x) and right (increasing x) from the current Z-value ''z'' are:
top = (((z & 0b10101010) − 1) & 0b10101010) , (z & 0b01010101)
bottom = (((z , 0b01010101) + 1) & 0b10101010) , (z & 0b01010101)
left = (((z & 0b01010101) − 1) & 0b01010101) , (z & 0b10101010)
right = (((z , 0b10101010) + 1) & 0b01010101) , (z & 0b10101010)
And in general to add two two-dimensional Z-values ''w'' and ''z'':
sum = ((z , 0b10101010) + (w & 0b01010101) & 0b01010101) , ((z , 0b01010101) + (w & 0b10101010) & 0b10101010)
Efficiently building quadtrees and octrees
The Z-ordering can be used to efficiently build aquadtree
A quadtree is a tree data structure in which each internal node has exactly four children. Quadtrees are the two-dimensional analog of octrees and are most often used to partition a two-dimensional space by recursively subdividing it into four ...
(2D) or octree
An octree is a tree data structure in which each internal node has exactly eight children. Octrees are most often used to partition a three-dimensional space by recursively subdividing it into eight octants. Octrees are the three-dimensional ana ...
(3D) for a set of points.. The basic idea is to sort the input set according to Z-order. Once sorted, the points can either be stored in a binary search tree and used directly, which is called a linear quadtree, or they can be used to build a pointer based quadtree.
The input points are usually scaled in each dimension to be positive integers, either as a fixed point representation over the unit range or corresponding to the machine word size. Both representations are equivalent and allow for the highest order non-zero bit to be found in constant time. Each square in the quadtree has a side length which is a power of two, and corner coordinates which are multiples of the side length. Given any two points, the ''derived square'' for the two points is the smallest square covering both points. The interleaving of bits from the ''x'' and ''y'' components of each point is called the ''shuffle'' of ''x'' and ''y'', and can be extended to higher dimensions.
Points can be sorted according to their shuffle without explicitly interleaving the bits. To do this, for each dimension, the most significant bit of the exclusive or
Exclusive or or exclusive disjunction is a logical operation that is true if and only if its arguments differ (one is true, the other is false).
It is symbolized by the prefix operator J and by the infix operators XOR ( or ), EOR, EXOR, , ...
of the coordinates of the two points for that dimension is examined. The dimension for which the most significant bit is largest is then used to compare the two points to determine their shuffle order.
The exclusive or operation masks off the higher order bits for which the two coordinates are identical. Since the shuffle interleaves bits from higher order to lower order, identifying the coordinate with the largest most significant bit, identifies the first bit in the shuffle order which differs, and that coordinate can be used to compare the two points.. This is shown in the following Python code:
less_msb function is modified to first compare the exponents. Only when they are equal is the standard less_msb function used on the mantissas.
Once the points are in sorted order, two properties make it easy to build a quadtree: The first is that the points contained in a square of the quadtree form a contiguous interval in the sorted order. The second is that if more than one child of a square contains an input point, the square is the ''derived square'' for two adjacent points in the sorted order.
For each adjacent pair of points, the derived square is computed and its side length determined. For each derived square, the interval containing it is bounded by the first larger square to the right and to the left in sorted order. Each such interval corresponds to a square in the quadtree. The result of this is a compressed quadtree, where only nodes containing input points or two or more children are present. A non-compressed quadtree can be built by restoring the missing nodes, if desired.
Rather than building a pointer based quadtree, the points can be maintained in sorted order in a data structure such as a binary search tree. This allows points to be added and deleted in time. Two quadtrees can be merged by merging the two sorted sets of points, and removing duplicates. Point location can be done by searching for the points preceding and following the query point in the sorted order. If the quadtree is compressed, the predecessor node found may be an arbitrary leaf inside the compressed node of interest. In this case, it is necessary to find the predecessor of the least common ancestor of the query point and the leaf found.
Use with one-dimensional data structures for range searching
Although preserving locality well, for efficient range searches an algorithm is necessary for calculating, from a point encountered in the data structure, the next Z-value which is in the multidimensional search range:UB-tree
The UB-tree as proposed by Rudolf Bayer and Volker Markl is a balanced tree for storing and efficiently retrieving multidimensional data. It is basically a B+ tree
A B+ tree is an m-ary tree with a variable but often large number of childre ...
s ("GetNextZ-address"). As the approach does not depend on the one dimensional data structure chosen, there is still free choice of structuring the data, so well known methods such as balanced trees can be used to cope with dynamic data (in contrast for example to R-tree
R-trees are tree data structures used for spatial access methods, i.e., for indexing multi-dimensional information such as geographical coordinates, rectangles or polygons. The R-tree was proposed by Antonin Guttman in 1984 and has found sign ...
s where special considerations are necessary). Similarly, this independence makes it easier to incorporate the method into existing databases.
Applying the method hierarchically (according to the data structure at hand), optionally in both increasing and decreasing direction, yields highly efficient multidimensional range search which is important in both commercial and technical applications, e.g. as a procedure underlying nearest neighbour searches. Z-order is one of the few multidimensional access methods that has found its way into commercial database systems (Oracle database
Oracle Database (commonly referred to as Oracle DBMS, Oracle Autonomous Database, or simply as Oracle) is a multi-model database management system produced and marketed by Oracle Corporation.
It is a database commonly used for running online t ...
1995, Transbase
Transbase is a relational database management system, developed and maintained by Transaction Software GmbH, Munich. The development of Transbase was started in the 1980s by Rudolf Bayer under the name „Merkur“ at the department of Computer S ...
2000 ).
As long ago as 1966, G.M.Morton proposed Z-order for file sequencing of a static two dimensional geographical database. Areal data units are contained in one or a few quadratic frames represented by their sizes and lower right corner Z-values, the sizes complying with the Z-order hierarchy at the corner position. With high probability, changing to an adjacent frame is done with one or a few relatively small scanning steps.
Related structures
As an alternative, theHilbert curve
The Hilbert curve (also known as the Hilbert space-filling curve) is a continuous fractal space-filling curve first described by the German mathematician David Hilbert in 1891, as a variant of the space-filling Peano curves discovered by Giuseppe ...
has been suggested as it has a better order-preserving behaviour, and, in fact, was used in an optimized index, the S2-geometry.
Applications
Linear algebra
TheStrassen algorithm
In linear algebra, the Strassen algorithm, named after Volker Strassen, is an algorithm for matrix multiplication. It is faster than the standard matrix multiplication algorithm for large matrices, with a better asymptotic complexity, although t ...
for matrix multiplication is based on splitting the matrices in four blocks, and then recursively splitting each of these blocks in four smaller blocks, until the blocks are single elements (or more practically: until reaching matrices so small that the Moser–de Bruijn sequence trivial algorithm is faster). Arranging the matrix elements in Z-order then improves locality, and has the additional advantage (compared to row- or column-major ordering) that the subroutine for multiplying two blocks does not need to know the total size of the matrix, but only the size of the blocks and their location in memory. Effective use of Strassen multiplication
with Z-order has been demonstrated, see Valsalam and Skjellum's 2002 paper.
Buluç ''et al.'' present a sparse matrix
In numerical analysis and scientific computing, a sparse matrix or sparse array is a matrix in which most of the elements are zero. There is no strict definition regarding the proportion of zero-value elements for a matrix to qualify as sparse b ...
data structure that Z-orders its non-zero elements to enable parallel
Parallel is a geometric term of location which may refer to:
Computing
* Parallel algorithm
* Parallel computing
* Parallel metaheuristic
* Parallel (software), a UNIX utility for running programs in parallel
* Parallel Sysplex, a cluster of ...
matrix-vector multiplication.
Texture mapping
SomeGPU
A graphics processing unit (GPU) is a specialized electronic circuit designed to manipulate and alter memory to accelerate the creation of images in a frame buffer intended for output to a display device. GPUs are used in embedded systems, mobi ...
s store texture map
Texture mapping is a method for mapping a texture on a computer-generated graphic. Texture here can be high frequency detail, surface texture, or color.
History
The original technique was pioneered by Edwin Catmull in 1974.
Texture mapping ...
s in Z-order to increase spatial locality of reference
In computer science, locality of reference, also known as the principle of locality, is the tendency of a processor to access the same set of memory locations repetitively over a short period of time. There are two basic types of reference localit ...
during texture mapped rasterization. This allows cache lines
A CPU cache is a hardware cache used by the central processing unit (CPU) of a computer to reduce the average cost (time or energy) to access data from the main memory. A cache is a smaller, faster memory, located closer to a processor core, whic ...
to represent rectangular tiles, increasing the probability that nearby accesses are in the cache. At a larger scale, it also decreases the probability of costly, so called, "page breaks" (i.e., the cost of changing rows) in SDRAM/DDRAM. This is important because 3D rendering involves arbitrary transformations (rotations, scaling, perspective, and distortion by animated surfaces).
These formats are often referred to as ''swizzled textures'' or ''twiddled textures''. Other tiled formats may also be used.
N-body problem
The Barnes–Hut algorithm requires construction of an oct-tree. Storing the data as a pointer-based tree requires many sequential pointer dereferences to iterate over the oct-tree indepth-first
Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible alon ...
order (expensive on a distributed-memory machine). Instead, if one stores the data in a hashtable
In computing, a hash table, also known as hash map, is a data structure that implements an associative array or dictionary. It is an abstract data type that maps keys to values. A hash table uses a hash function to compute an ''index'', also ...
, using oct-tree hashing
An octree is a tree data structure in which each internal node has exactly eight children. Octrees are most often used to partition a three-dimensional space by recursively subdividing it into eight octants. Octrees are the three-dimensional anal ...
, the Z-order curve naturally iterates the oct-tree in depth-first order.
See also
*Geohash
Geohash is a public domain geocode system invented in 2008 by Gustavo NiemeyerEvidences at the Wayback Machine:
labix.org in 2008, the G. Niemeyer's blog announcing Geohash
*an article about Geohash witnessing and citing G. Niemeyer works, befor ...
* Hilbert R-tree Hilbert R-tree, an R-tree variant, is an index for multidimensional objects such as lines, regions, 3-D objects, or high-dimensional feature-based parametric objects. It can be thought of as an extension to B+-tree for multidimensional objects.
Th ...
* Linear algebra
Linear algebra is the branch of mathematics concerning linear equations such as:
:a_1x_1+\cdots +a_nx_n=b,
linear maps such as:
:(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n,
and their representations in vector spaces and through matrices.
...
* Locality preserving hashing
* Matrix representation
Matrix representation is a method used by a computer language to store matrix (mathematics), matrices of more than one dimension in computer storage, memory.
Fortran and C (programming language), C use different schemes for their native arrays. Fo ...
* Netto's theorem
In mathematical analysis, Netto's theorem states that continuous bijections of smooth manifolds preserve dimension. That is, there does not exist a continuous bijection between two smooth manifolds of different dimension. It is named after Eugen N ...
* PH-tree
* Spatial index
A spatial database is a general-purpose database (usually a relational database) that has been enhanced to include spatial data that represents objects defined in a geometric space, along with tools for querying and analyzing such data. Most sp ...
References
{{reflistExternal links
STANN: A library for approximate nearest neighbor search, using Z-order curve
Sean Eron Anderson, Stanford University Fractal curves Database algorithms Geometric data structures Database index techniques Linear algebra