HOME

TheInfoList



Click Here for Items Related To - Midpoint circle algorithm
OR:
Midpoint circle algorithm on:   [Wikipedia]   [Google]   [Amazon]

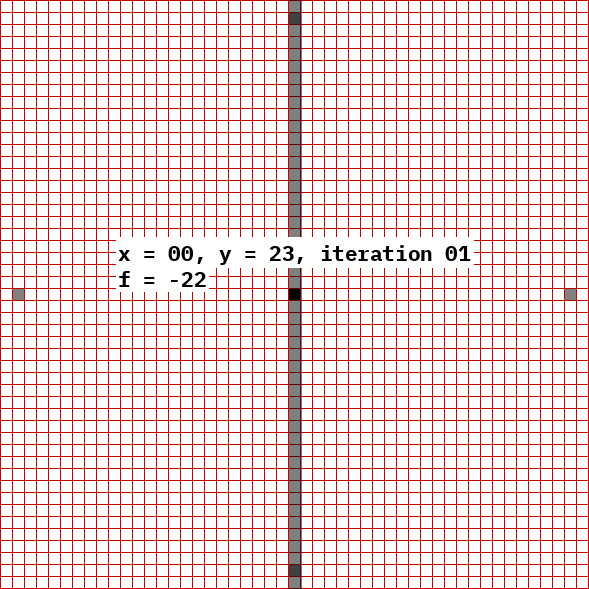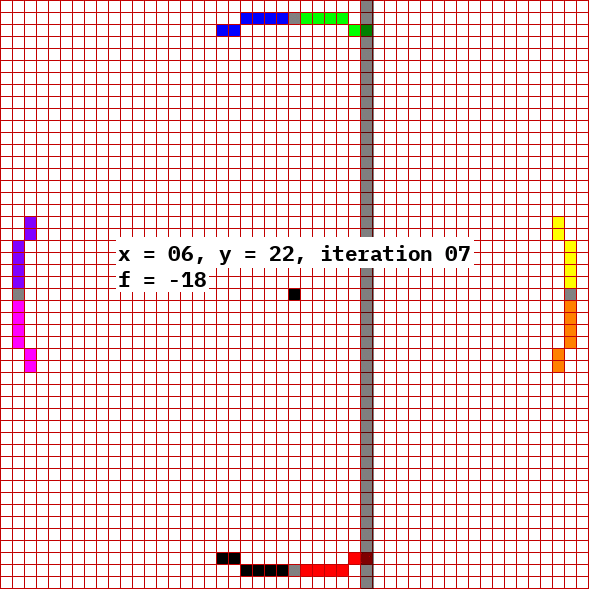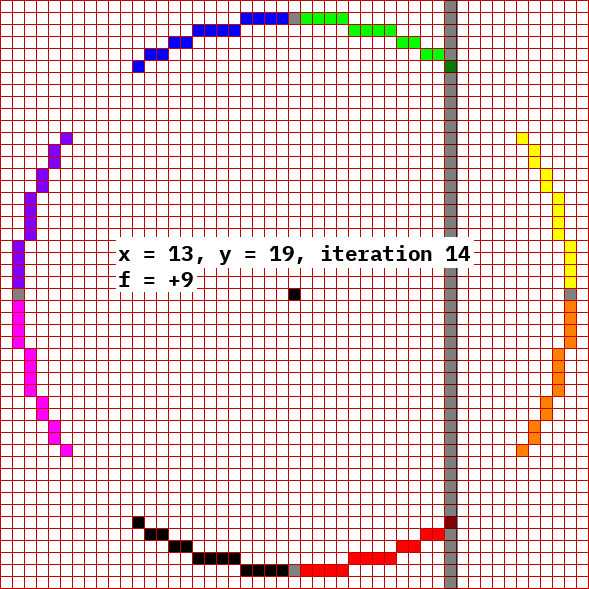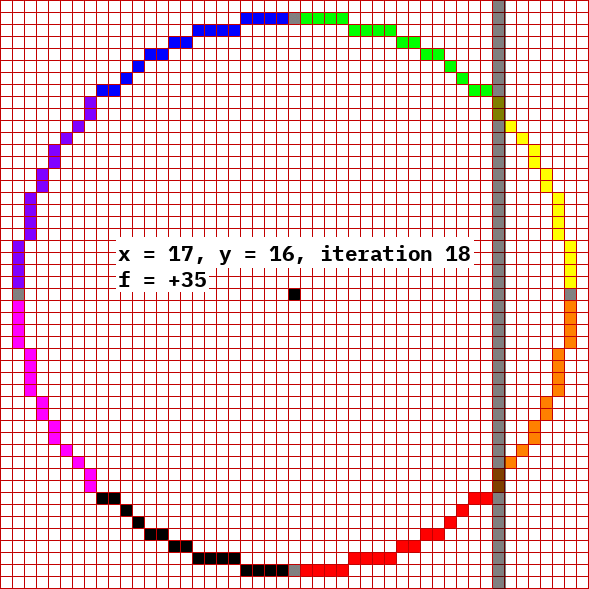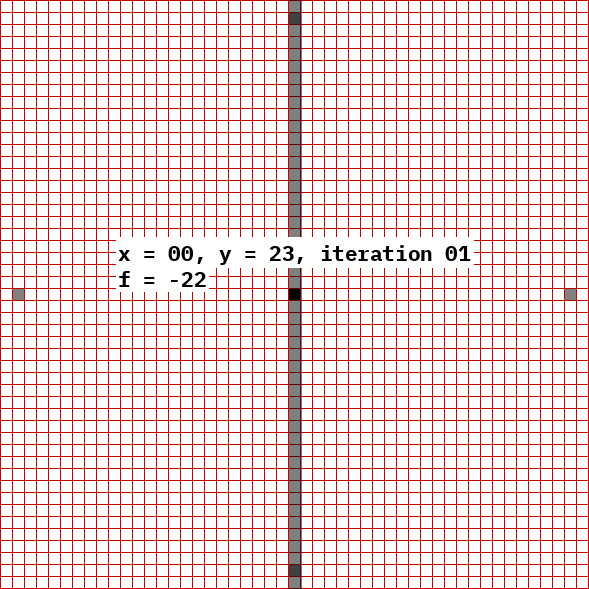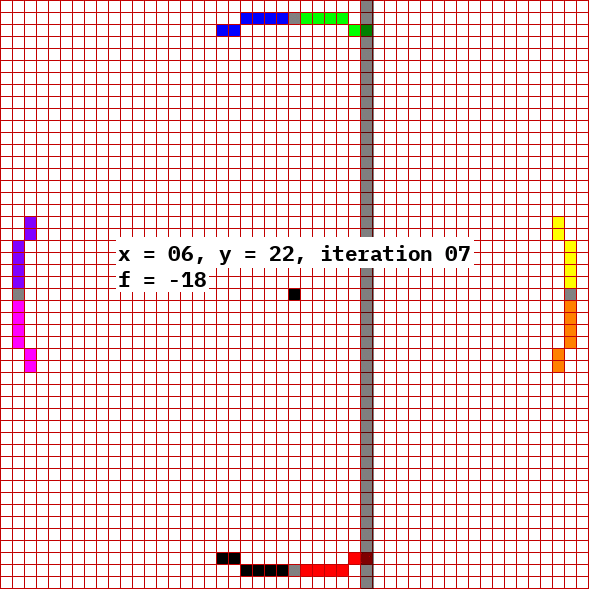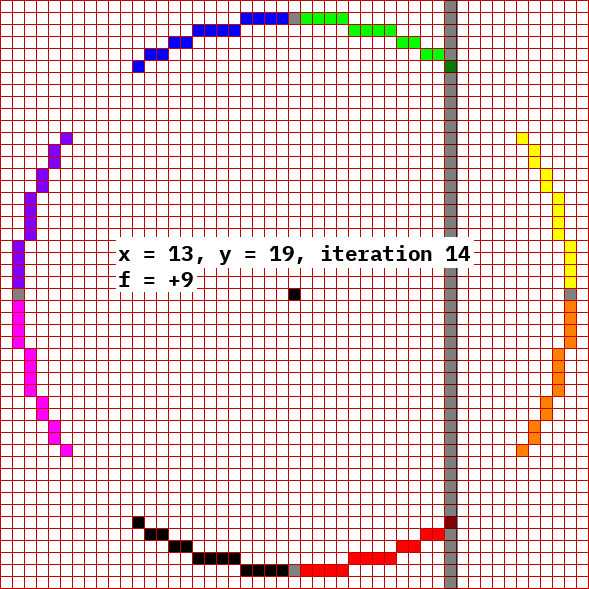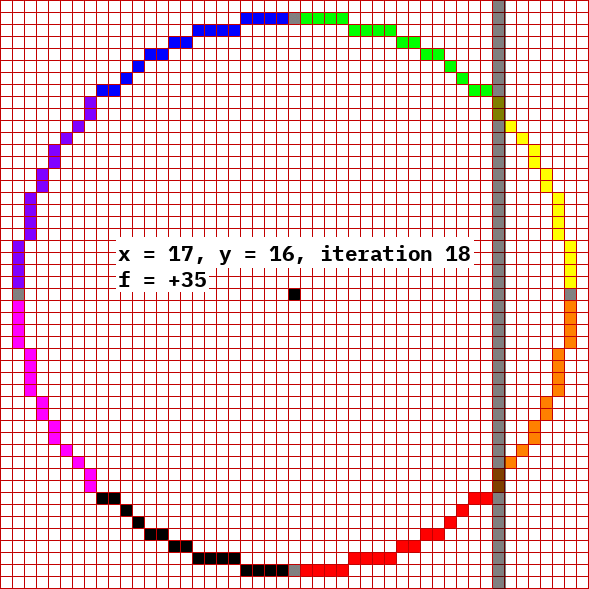In
computer graphics Computer graphics deals with generating images with the aid of computers. Today, computer graphics is a core technology in digital photography, film, video games, cell phone and computer displays, and many specialized applications. A great de ...
, the midpoint circle algorithm is an algorithm used to determine the points needed for
rasterizing In computer graphics, rasterisation (British English) or rasterization (American English) is the task of taking an image described in a vector graphics format (shapes) and converting it into a raster image (a series of pixels, dots or lines, whic ...
a
circle A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is const ...
.
Bresenham Jack Elton Bresenham (born 11 October 1937, Clovis, New Mexico, US) is a former professor of computer science. Biography Bresenham retired from 27 years of service at IBM as a Senior Technical Staff Member in 1987. He taught for 16 years at Wint ...
's circle algorithm is derived from the midpoint circle algorithm. The algorithm can be generalized to
conic section In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a specia ...
s. The algorithm is related to work by Pitteway and Van Aken.


Summary

This algorithm draws all eight octants simultaneously, starting from each cardinal direction (0°, 90°, 180°, 270°) and extends both ways to reach the nearest multiple of 45° (45°, 135°, 225°, 315°). It can determine where to stop because when y = x, it has reached 45°. The reason for using these angles is shown in the above picture: As x increases, it does not skip nor repeat any x value until reaching 45°. So during the while loop, x increments by 1 each iteration, and y decrements by 1 on occasion, never exceeding 1 in one iteration. This changes at 45° because that is the point where the tangent is rise=run. Whereas rise>run before and riseconcentric circles In geometry, two or more objects are said to be concentric, coaxal, or coaxial when they share the same center or axis. Circles, regular polygons and regular polyhedra, and spheres may be concentric to one another (sharing the same center point ...
drawn with the midpoint circle algorithm." heights="191px"> File:Concentric circles drawn with Bresenham's circle algorithm (all black) 01.png, On left, all circles are drawn black. File:Concentric circles drawn with Bresenham's circle algorithm.png, On right, red, black and blue are used together to demonstrate the concentricity of the circles.


Algorithm

The objective of the algorithm is to approximate the curve x^2 + y^2 = r^2 using pixels; in
layman's terms Plain English (or layman's terms) are groups of words that are to be clear and easy to know. It usually avoids the use of rare words and uncommon euphemisms to explain the subject. Plain English wording is intended to be suitable for almost anyone, ...
every pixel should be approximately the same distance from the center. At each step, the path is extended by choosing the adjacent pixel which satisfies x^2 + y^2 \leq r^2 but maximizes x^2 + y^2 . Since the candidate pixels are adjacent, the arithmetic to calculate the latter expression is simplified, requiring only bit shifts and additions. But a simplification can be done in order to understand the bitshift. Keep in mind that a left bitshift of a binary number is the same as multiplying with 2. Ergo, a left bitshift of the radius only produces the
diameter In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle. It can also be defined as the longest chord of the circle. Both definitions are also valid for ...
which is defined as radius times two. This algorithm starts with the
circle A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is const ...
equation. For simplicity, assume the center of the circle is at (0,0). Consider first the first octant only, and draw a curve which starts at point (r,0) and proceeds counterclockwise, reaching the angle of 45. The ''fast'' direction here (the
basis vector In mathematics, a set of vectors in a vector space is called a basis if every element of may be written in a unique way as a finite linear combination of elements of . The coefficients of this linear combination are referred to as components ...
with the greater increase in value) is the y direction. The algorithm always takes a step in the positive y direction (upwards), and occasionally takes a step in the ''slow'' direction (the negative x direction). From the circle equation is obtained the transformed equation x^2 + y^2 - r^2 = 0, where r^2 is computed only once during initialization. Let the points on the circle be a sequence of coordinates of the vector to the point (in the usual basis). Points are numbered according to the order in which drawn, with n=1 assigned to the first point (r,0). For each point, the following holds: :\begin x_n^2 + y_n^2 = r^2 \end This can be rearranged thus: :\begin x_n^2 = r^2 - y_n^2 \end And likewise for the next point: :\begin x_^2 = r^2 - y_^2 \end Since for the first octant the next point will always be at least 1 pixel higher than the last (but also at most 1 pixel higher to maintain continuity), it is true that: :\begin y_^2 &= (y_n + 1)^2 \\ &= y_n^2 + 2y_n + 1 \end :\begin x_^2 = r^2 - y_n^2 - 2y_n - 1 \end So, rework the next-point-equation into a recursive one by substituting x_n^2 = r^2 - y_n^2: :\begin x_^2 = x_n^2 - 2y_n - 1 \end Because of the continuity of a circle and because the maxima along both axes is the same, clearly it will not be skipping x points as it advances in the sequence. Usually it stays on the same x coordinate, and sometimes advances by one. The resulting coordinate is then translated by adding midpoint coordinates. These frequent integer additions do not limit the
performance A performance is an act of staging or presenting a play, concert, or other form of entertainment. It is also defined as the action or process of carrying out or accomplishing an action, task, or function. Management science In the work place ...
much, as those square (root) computations can be spared in the inner loop in turn. Again, the zero in the transformed circle equation is replaced by the error term. The initialization of the error term is derived from an offset of ½ pixel at the start. Until the intersection with the perpendicular line, this leads to an accumulated value of r in the error term, so that this value is used for initialization. The frequent computations of
square In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adj ...
s in the circle equation,
trigonometric Trigonometry () is a branch of mathematics that studies relationships between side lengths and angles of triangles. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. ...
expressions and
square root In mathematics, a square root of a number is a number such that ; in other words, a number whose ''square'' (the result of multiplying the number by itself, or  ⋅ ) is . For example, 4 and −4 are square roots of 16, because . E ...
s can again be avoided by dissolving everything into single steps and using recursive computation of the quadratic terms from the preceding iterations.


Variant with integer-based arithmetic

Just as with
Bresenham's line algorithm Bresenham's line algorithm is a line drawing algorithm that determines the points of an ''n''-dimensional raster that should be selected in order to form a close approximation to a straight line between two points. It is commonly used to draw line ...
, this algorithm can be optimized for integer-based math. Because of symmetry, if an algorithm can be found that only computes the pixels for one octant, the pixels can be reflected to get the whole circle. We start by defining the radius error as the difference between the exact representation of the circle and the center point of each pixel (or any other arbitrary mathematical point on the pixel, so long as it's consistent across all pixels). For any pixel with a center at (x_i, y_i), the radius error is defined as: :RE(x_i,y_i) = \left\vert x_i^2 + y_i^2 - r^2 \right\vert For clarity, this formula for a circle is derived at the origin, but the algorithm can be modified for any location. It is useful to start with the point (r,0) on the positive X-axis. Because the radius will be a whole number of pixels, clearly the radius error will be zero: :RE(x_i,y_i) = \left\vert x_i^2 + 0^2 - r^2 \right\vert = 0 Because it starts in the first counter-clockwise positive octant, it will step in the direction with the greatest ''travel'', the Y direction, so it is clear that y_ = y_i + 1. Also, because it concerns this octant only, the X values have only 2 options: to stay the same as the prior iteration, or decrease by 1. A decision variable can be created that determines if the following is true: :RE(x_i-1, y_i+1) < RE(x_i,y_i+1) If this inequality holds, then plot (x_i-1, y_i+1); if not, then plot (x_i,y_i+1). So, how to determine if this inequality holds? Start with a definition of radius error: : \begin RE(x_i-1, y_i+1) & < RE(x_i,y_i+1) \\ \left\vert (x_i-1)^2 + (y_i+1)^2 - r^2 \right\vert & < \left\vert x_i^2 + (y_i+1)^2 - r^2 \right\vert \\ \left\vert (x_i^2 - 2 x_i + 1) + (y_i^2 + 2 y_i + 1) - r^2 \right\vert & < \left\vert x_i^2 + (y_i^2 + 2 y_i + 1) - r^2 \right\vert \\ \end The absolute value function does not help, so square both sides, since a square is always positive: : \begin \left (x_i^2 - 2 x_i + 1) + (y_i^2 + 2 y_i + 1) - r^2 \right 2 & < \left x_i^2 + (y_i^2 + 2 y_i + 1) - r^2 \right 2 \\ \left (x_i^2 + y_i^2 - r^2 + 2 y_i + 1) + (1 - 2 x_i) \right 2 & < \left x_i^2 + y_i^2 - r^2 + 2 y_i + 1 \right 2 \\ \left ( x_i^2 + y_i^2 - r^2 + 2 y_i + 1 \right )^2 + 2 (1 - 2 x_i) (x_i^2 + y_i^2 - r^2 + 2 y_i + 1) + (1 - 2 x_i)^2 & < \left x_i^2 + y_i^2 - r^2 + 2 y_i + 1 \right 2 \\ 2 (1 - 2 x_i) (x_i^2 + y_i^2 - r^2 + 2 y_i + 1) + (1 - 2 x_i)^2 & < 0 \\ \end Since x > 0, the term (1 - 2 x_i) < 0, so dividing gets: : \begin 2 \left (x_i^2 + y_i^2 - r^2) + (2 y_i + 1) \right + (1 - 2 x_i) & > 0 \\ 2 \left RE(x_i,y_i) + Y_\text \right + X_\text & > 0 \\ \end Thus, the decision criterion changes from using floating-point operations to simple integer addition, subtraction, and bit shifting (for the multiply by 2 operations). If , then decrement the X value. If , then keep the same X value. Again, by reflecting these points in all the octants, a full circle results. We may reduce computation by only calculating the delta between the values of this decision formula from its value at the previous step. We start by assigning as which is the initial value of the formula at , then as above at each step if we update it as (and decrement X), otherwise thence increment Y as usual.


Drawing incomplete octants

The implementations above always draw only complete octants or circles. To draw only a certain
arc ARC may refer to: Business * Aircraft Radio Corporation, a major avionics manufacturer from the 1920s to the '50s * Airlines Reporting Corporation, an airline-owned company that provides ticket distribution, reporting, and settlement services * ...
from an angle \alpha to an angle \beta, the algorithm needs first to calculate the x and y coordinates of these end points, where it is necessary to resort to trigonometric or square root computations (see
Methods of computing square roots Methods of computing square roots are numerical analysis algorithms for approximating the principal, or non-negative, square root (usually denoted \sqrt, \sqrt /math>, or S^) of a real number. Arithmetically, it means given S, a procedure for fin ...
). Then the Bresenham algorithm is run over the complete octant or circle and sets the pixels only if they fall into the wanted interval. After finishing this arc, the algorithm can be ended prematurely. If the angles are given as
slope In mathematics, the slope or gradient of a line is a number that describes both the ''direction'' and the ''steepness'' of the line. Slope is often denoted by the letter ''m''; there is no clear answer to the question why the letter ''m'' is use ...
s, then no trigonometry or square roots are necessary: simply check that y/x is between the desired slopes.


Generalizations

It is also possible to use the same concept to rasterize a
parabola In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves. One descript ...
,
ellipse In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special ty ...
, or any other two-dimensional
curve In mathematics, a curve (also called a curved line in older texts) is an object similar to a line (geometry), line, but that does not have to be Linearity, straight. Intuitively, a curve may be thought of as the trace left by a moving point (ge ...
.


References

{{Reflist


External links


Drawing circles
- An article on drawing circles, that derives from a simple scheme to an efficient one
Midpoint Circle Algorithm in several programming languages
Geometric algorithms Digital geometry Articles with example C code Articles with example JavaScript code de:Rasterung von Kreisen#Midpoint-Algorithmus