Maple (software) on:
[Wikipedia]
[Google]
[Amazon]
Maple is a
myfac := proc(n::nonnegint)
local out, i;
out := 1;
for i from 2 to n do
out := out * i
end do;
out
end proc;
Simple functions can also be defined using the "maps to" arrow notation:
myfac := n -> product(i, i = 1..n);
int(cos(x/a), x);
Output:
:
M := Matrix(
:
LinearAlgebra:-Determinant(M);
:
series(tanh(x), x = 0, 15)
:
:
f := x^53-88*x^5-3*x-5 = 0
fsolve(f)
-1.097486315, -.5226535640, 1.099074017
The same command can also solve systems of equations:
f := (cos(x+y))^2 + exp(x)*y+cot(x-y)+cosh(z+x) = 0:
g := x^5 - 8*y = 2:
h := x+3*y-77*z=55;
fsolve( );
plot(x*sin(x), x = -10..10);
plot3d(x^2+y^2, x = -1..1, y = -1..1);
plots:-animate(subs(k = 0.5, f), x=-30..30, t=-10..10, numpoints=200, frames=50, color=red, thickness=3);
 * Animation of functions of three variables
* Animation of functions of three variables
plots:-animate3d(cos(t*x)*sin(3*t*y), x=-Pi..Pi, y=-Pi..Pi, t=1..2);
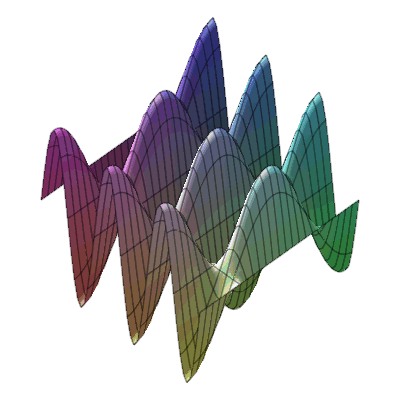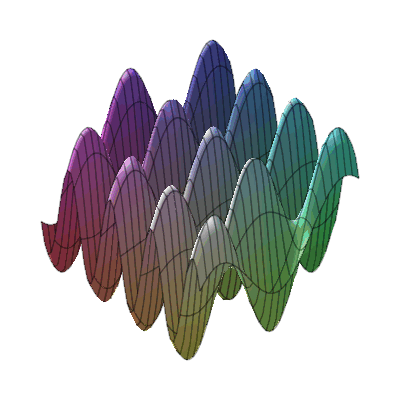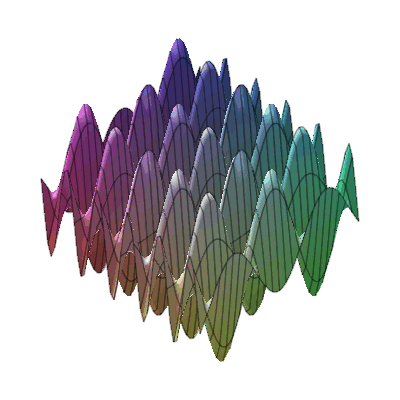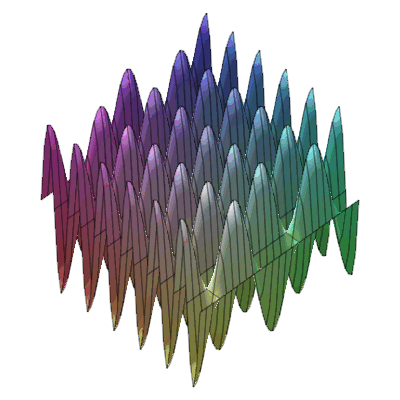 * Fly-through animation of 3-D plots.
* Fly-through animation of 3-D plots.
M := Matrix( 400,400,200

f := (1+A*t+B*t^2)*exp(c*t);
:
inttrans:-laplace(f, t, s);
:
* inverse Laplace transform
inttrans:-invlaplace(1/(s-a), s, x);
:
inttrans:-fourier(sin(x), x, w)
:
eqn:= f(x)-3*Int((x*y+x^2*y^2)*f(y), y=-1..1) = h(x):
intsolve(eqn,f(x));
:
Maplesoft, division of Waterloo Maple, Inc.
– official website {{Authority control C (programming language) software Notebook interface Computer algebra system software for Linux Computer algebra system software for macOS Computer algebra system software for Windows Computer algebra systems Cross-platform software Data mining and machine learning software Data visualization software Data-centric programming languages Econometrics software Functional languages Interactive geometry software IRIX software Linear algebra Maplesoft Mathematical optimization software Mathematical software Numerical analysis software for Linux Numerical analysis software for macOS Numerical analysis software for Windows Numerical programming languages Numerical software Parallel computing Physics software Plotting software Products introduced in 1982 Proprietary commercial software for Linux Proprietary cross-platform software Regression and curve fitting software Simulation programming languages Software modeling language Statistical programming languages Theorem proving software systems Time series software
symbolic
Symbolic may refer to:
* Symbol, something that represents an idea, a process, or a physical entity
Mathematics, logic, and computing
* Symbolic computation, a scientific area concerned with computing with mathematical formulas
* Symbolic dynamic ...
and numeric
A number is a mathematical object used to count, measure, and label. The original examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers can ...
computing environment as well as a multi-paradigm programming language
Programming paradigms are a way to classify programming languages based on their features. Languages can be classified into multiple paradigms.
Some paradigms are concerned mainly with implications for the execution model of the language, suc ...
. It covers several areas of technical computing, such as symbolic mathematics, numerical analysis, data processing, visualization, and others. A toolbox, MapleSim, adds functionality for multidomain physical modeling and code generation.
Maple's capacity for symbolic computing include those of a general-purpose computer algebra system. For instance, it can manipulate mathematical expressions and find symbolic solutions to
certain problems, such as those arising from ordinary and partial differential equations
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, a ...
.
Maple is developed commercially by the Canadian software company Maplesoft. The name 'Maple' is a reference to the software's Canadian heritage.
Overview
Core functionality
Users can enter mathematics in traditional mathematical notation. Custom user interfaces can also be created. There is support for numeric computations, to arbitrary precision, as well as symbolic computation and visualization. Examples of symbolic computations are given below. Maple incorporates a dynamically typed imperative-styleprogramming language
A programming language is a system of notation for writing computer programs. Most programming languages are text-based formal languages, but they may also be graphical. They are a kind of computer language.
The description of a programming l ...
(resembling Pascal), which permits variables of lexical scope
Scope or scopes may refer to:
People with the surname
* Jamie Scope (born 1986), English footballer
* John T. Scopes (1900–1970), central figure in the Scopes Trial regarding the teaching of evolution
Arts, media, and entertainment
* CinemaS ...
. There are also interfaces to other languages ( C, C#, Fortran, Java
Java (; id, Jawa, ; jv, ꦗꦮ; su, ) is one of the Greater Sunda Islands in Indonesia. It is bordered by the Indian Ocean to the south and the Java Sea to the north. With a population of 151.6 million people, Java is the world's mo ...
, MATLAB
MATLAB (an abbreviation of "MATrix LABoratory") is a proprietary multi-paradigm programming language and numeric computing environment developed by MathWorks. MATLAB allows matrix manipulations, plotting of functions and data, implementa ...
, and Visual Basic), as well as to Microsoft Excel
Microsoft Excel is a spreadsheet developed by Microsoft for Windows, macOS, Android and iOS. It features calculation or computation capabilities, graphing tools, pivot tables, and a macro programming language called Visual Basic for ...
.
Maple supports MathML 2.0, which is a W3C format for representing and interpreting mathematical expressions, including their display in web pages. There is also functionality for converting expressions from traditional mathematical notation to markup suitable for the typesetting system LaTeX
Latex is an emulsion (stable dispersion) of polymer microparticles in water. Latexes are found in nature, but synthetic latexes are common as well.
In nature, latex is found as a milky fluid found in 10% of all flowering plants (angiosper ...
.
Architecture
Maple is based on a smallkernel
Kernel may refer to:
Computing
* Kernel (operating system), the central component of most operating systems
* Kernel (image processing), a matrix used for image convolution
* Compute kernel, in GPGPU programming
* Kernel method, in machine lea ...
, written in C, which provides the Maple language. Most functionality is provided by libraries, which come from a variety of sources. Most of the libraries are written in the Maple language; these have viewable source code. Many numerical computations are performed by the NAG Numerical Libraries, ATLAS
An atlas is a collection of maps; it is typically a bundle of maps of Earth or of a region of Earth.
Atlases have traditionally been bound into book form, but today many atlases are in multimedia formats. In addition to presenting geograp ...
libraries, or GMP libraries.
Different functionality in Maple requires numerical data in different formats. Symbolic expressions are stored in memory as directed acyclic graphs. The standard interface and calculator interface are written in Java
Java (; id, Jawa, ; jv, ꦗꦮ; su, ) is one of the Greater Sunda Islands in Indonesia. It is bordered by the Indian Ocean to the south and the Java Sea to the north. With a population of 151.6 million people, Java is the world's mo ...
.
History
The first concept of Maple arose from a meeting in late 1980 at the University of Waterloo. Researchers at the university wished to purchase a computer powerful enough to run the Lisp-based computer algebra system Macsyma. Instead, they opted to develop their own computer algebra system, named Maple, that would run on lower cost computers. Aiming for portability, they began writing Maple in programming languages from the BCPL family (initially using a subset of B and C, and later on only C). A first limited version appeared after three weeks, and fuller versions entered mainstream use beginning in 1982. By the end of 1983, over 50 universities had copies of Maple installed on their machines. In 1984, the research group arranged with Watcom Products Inc to license and distribute the first commercially available version, Maple 3.3. In 1988 Waterloo Maple Inc. (Maplesoft) was founded. The company’s original goal was to manage the distribution of the software, but eventually it grew to have its own R&D department, where most of Maple's development takes place today (the remainder being done at various university laboratories). In 1989, the first graphical user interface for Maple was developed and included with version 4.3 for the Macintosh. X11 and Windows versions of the new interface followed in 1990 with Maple V. In 1992, Maple V Release 2 introduced the Maple "worksheet" that combined text, graphics, and input and typeset output. In 1994 a special issue of a newsletter created by Maple developers called ''MapleTech'' was published. In 1999, with the release of Maple 6, Maple included some of the NAG Numerical Libraries. In 2003, the current "standard" interface was introduced with Maple 9. This interface is primarily written inJava
Java (; id, Jawa, ; jv, ꦗꦮ; su, ) is one of the Greater Sunda Islands in Indonesia. It is bordered by the Indian Ocean to the south and the Java Sea to the north. With a population of 151.6 million people, Java is the world's mo ...
(although portions, such as the rules for typesetting mathematical formulae, are written in the Maple language). The Java interface was criticized for being slow; improvements have been made in later versions, although the Maple 11 documentation recommends the previous ("classic") interface for users with less than 500 MB of physical memory.
Between 1995 and 2005 Maple lost significant market share to competitors due to a weaker user interface. With Maple 10 in 2005, Maple introduced a new "document mode" interface, which has since been further developed across several releases.
In September 2009 Maple and Maplesoft were acquired by the Japanese software retailer Cybernet Systems.
Version history
* Maple 1.0: January, 1982 * Maple 1.1: January, 1982 * Maple 2.0: May, 1982 * Maple 2.1: June, 1982 * Maple 2.15: August, 1982 * Maple 2.2: December, 1982 * Maple 3.0: May, 1983 * Maple 3.1: October, 1983 * Maple 3.2: April, 1984 * Maple 3.3: March, 1985 (first public available version) * Maple 4.0: April, 1986 * Maple 4.1: May, 1987 * Maple 4.2: December, 1987 * Maple 4.3: March, 1989 * Maple V: August, 1990 * Maple V R2: November 1992 * Maple V R3: March 15, 1994 * Maple V R4: January, 1996 * Maple V R5: November 1, 1997 * Maple 6: December 6, 1999 * Maple 7: July 1, 2001 * Maple 8: April 16, 2002 * Maple 9: June 30, 2003 * Maple 9.5: April 15, 2004 * Maple 10: May 10, 2005 * Maple 11: February 21, 2007 * Maple 11.01: July, 2007 * Maple 11.02: November, 2007 * Maple 12: May, 2008 * Maple 12.01: October, 2008 * Maple 12.02: December, 2008 * Maple 13: April 28, 2009 * Maple 13.01: July, 2009 * Maple 13.02: October, 2009 * Maple 14: April 29, 2010 * Maple 14.01: October 28, 2010 * Maple 15: April 13, 2011 * Maple 15.01: June 21, 2011 * Maple 16: March 28, 2012 * Maple 16.01: May 16, 2012 * Maple 17: March 13, 2013 * Maple 17.01: July, 2013 * Maple 18: Mar 5, 2014 * Maple 18.01: May, 2014 * Maple 18.01a: July, 2014 * Maple 18.02: Nov, 2014 * Maple 2015.0: Mar 4, 2015 * Maple 2015.1: Nov, 2015 * Maple 2016.0: March 2, 2016 * Maple 2016.1: April 20, 2016 * Maple 2016.1a: April 27, 2016 * Maple 2017.0: May 25, 2017 * Maple 2017.1: June 28, 2017 * Maple 2017.2: August 2, 2017 * Maple 2017.3: October 3, 2017 * Maple 2018.0: March 21, 2018 * Maple 2019.0: March 14, 2019 * Maple 2020.0: March 12, 2020Features
Features of Maple include: * Support for symbolic and numeric computation with arbitrary precision * Elementary and special mathematical function libraries *Complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
s and interval arithmetic
* Arithmetic, greatest common divisors and factorization for multivariate polynomials over the rationals, finite fields, algebraic number fields, and algebraic function fields
* Limits, series and asymptotic expansions
* Gröbner basis
* Differential Algebra
* Matrix manipulation tools including support for sparse arrays
* Mathematical function graphing and animation tools
* Solvers for systems of equations, diophantine equations, ODEs, PDEs, DAEs, DDEs and recurrence relations
* Numeric and symbolic tools for discrete and continuous calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizati ...
including definite and indefinite integration, definite and indefinite sum In discrete calculus the indefinite sum operator (also known as the antidifference operator), denoted by \sum _x or \Delta^ , is the linear operator
In mathematics, and more specifically in linear algebra, a linear map (also called a linear ma ...
mation, automatic differentiation and continuous and discrete integral transforms
* Constrained and unconstrained local and global optimization
* Statistics including model fitting, hypothesis testing, and probability distribution
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomeno ...
s
* Tools for data manipulation, visualization and analysis
* Tools for probability and combinatoric
Combinatorics is an area of mathematics primarily concerned with counting, both as a means and an end in obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many appl ...
problems
* Support for time-series and unit based data
* Connection to online collection of financial and economic data
* Tools for financial calculations including bonds, annuities, derivatives, options etc.
* Calculations and simulations on random processes
* Tools for text mining including regular expressions
* Tools for signal processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing '' signals'', such as sound, images, and scientific measurements. Signal processing techniques are used to optimize transmissions, ...
and linear and non-linear control system
A control system manages, commands, directs, or regulates the behavior of other devices or systems using control loops. It can range from a single home heating controller using a thermostat controlling a domestic boiler to large industrial ...
s
* Discrete math
Discrete mathematics is the study of mathematical structures that can be considered "discrete" (in a way analogous to discrete variables, having a bijection with the set of natural numbers) rather than "continuous" (analogously to continuous ...
tools including number theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Math ...
* Tools for visualizing and analysing directed and undirected graphs
* Group theory including permutation and finitely presented groups
* Symbolic tensor functions
* Import and export filters for data, image, sound, CAD, and document formats
* Technical word processing including formula editing
* Programming language supporting procedural
Procedural may refer to:
* Procedural generation, a term used in computer graphics applications
*Procedural knowledge, the knowledge exercised in the performance of some task
* Procedural law, a legal concept
*Procedural memory, a cognitive scienc ...
, functional and object-oriented constructs
* Tools for adding user interface
In the industrial design field of human–computer interaction, a user interface (UI) is the space where interactions between humans and machines occur. The goal of this interaction is to allow effective operation and control of the machine f ...
s to calculations and applications
* Tools for connecting to SQL, Java
Java (; id, Jawa, ; jv, ꦗꦮ; su, ) is one of the Greater Sunda Islands in Indonesia. It is bordered by the Indian Ocean to the south and the Java Sea to the north. With a population of 151.6 million people, Java is the world's mo ...
, .NET, C++, Fortran and http
The Hypertext Transfer Protocol (HTTP) is an application layer protocol in the Internet protocol suite model for distributed, collaborative, hypermedia information systems. HTTP is the foundation of data communication for the World Wide Web, ...
* Tools for generating code for C, C#, Fortran, Java
Java (; id, Jawa, ; jv, ꦗꦮ; su, ) is one of the Greater Sunda Islands in Indonesia. It is bordered by the Indian Ocean to the south and the Java Sea to the north. With a population of 151.6 million people, Java is the world's mo ...
, JavaScript
JavaScript (), often abbreviated as JS, is a programming language that is one of the core technologies of the World Wide Web, alongside HTML and CSS. As of 2022, 98% of Website, websites use JavaScript on the Client (computing), client side ...
, Julia, Matlab
MATLAB (an abbreviation of "MATrix LABoratory") is a proprietary multi-paradigm programming language and numeric computing environment developed by MathWorks. MATLAB allows matrix manipulations, plotting of functions and data, implementa ...
, Perl
Perl is a family of two High-level programming language, high-level, General-purpose programming language, general-purpose, Interpreter (computing), interpreted, dynamic programming languages. "Perl" refers to Perl 5, but from 2000 to 2019 it ...
, Python, R, and Visual Basic
* Tools for parallel programming
Parallel computing is a type of computation in which many calculations or processes are carried out simultaneously. Large problems can often be divided into smaller ones, which can then be solved at the same time. There are several different f ...
Examples of Maple code
The following code, which computes the factorial of a nonnegative integer, is an example of an imperative programming construct within Maple:Integration
Find :.Determinant
Compute the determinant of a matrix.1,2,3 1-2-3; 1, 2, 3; or One, Two, Three may refer to:
Brands
* 1-2-3 (fuel station), in Norway
* Lotus 1-2-3, a computer spreadsheet program
* .123, a file extension used by Lotus 1-2-3
* Jell-O 1-2-3, a dessert
Film, TV and books
* ''One, Two, Three'' ...
,b,c ,y,z); # example Matrix
Series expansion
Solve equations numerically
The following code numerically calculates the roots of a high-order polynomial:Plotting of function of single variable
Plot with ranging from -10 to 10:Plotting of function of two variables
Plot with and ranging from -1 to 1:Animation of functions
* Animation of function of two variables : * Animation of functions of three variables
* Animation of functions of three variables
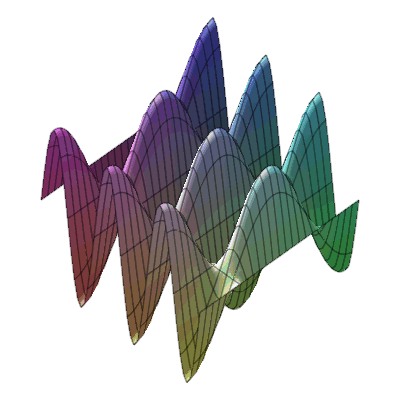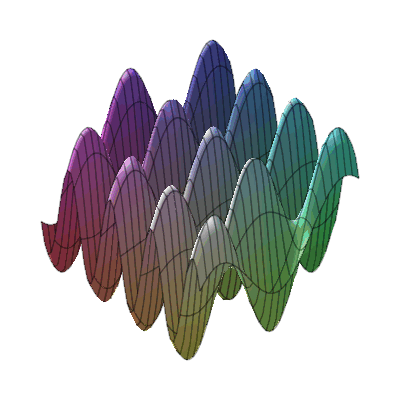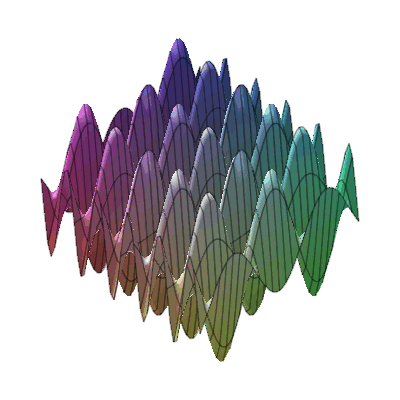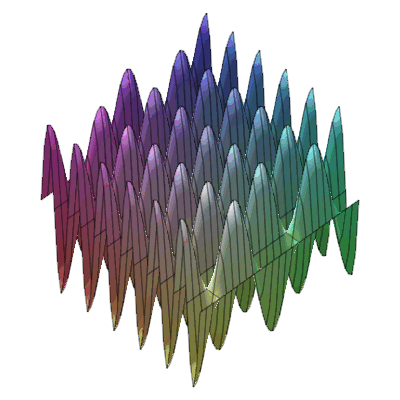 * Fly-through animation of 3-D plots.
* Fly-through animation of 3-D plots.
00,100,-400
This list contains selected positive numbers in increasing order, including counts of things, dimensionless quantities and probabilities. Each number is given a name in the short scale, which is used in English-speaking countries, as well as a ...
,1,1, datatype=float :
plot3d(1, x=0..2*Pi, y=0..Pi, axes=none, coords=spherical, viewpoint= ath=M;

Laplace transform
* Laplace transformFourier transform
* Fourier transformIntegral equations
Find functions that satisfy the integral equation :.Use of the Maple engine
The Maple engine is used within several other products from Maplesoft: * Moebius, DigitalEd’s online testing suite, uses Maple to algorithmically generate questions and grade student responses. * MapleNet allows users to create JSP pages andJava
Java (; id, Jawa, ; jv, ꦗꦮ; su, ) is one of the Greater Sunda Islands in Indonesia. It is bordered by the Indian Ocean to the south and the Java Sea to the north. With a population of 151.6 million people, Java is the world's mo ...
Applets. MapleNet 12 and above also allow users to upload and work with Maple worksheets containing interactive components.
* MapleSim, an engineering simulation tool.
* Maple Quantum Chemistry Package from RDMChem computes and visualizes the electronic energies and properties of molecules.
Listed below are third-party commercial products that no longer use the Maple engine:
* Versions of Mathcad
Mathcad is computer software for the verification, validation, documentation and re-use of mathematical calculations in engineering and science, notably mechanical, chemical, electrical, and civil engineering. Released in 1986 on DOS, it introduce ...
released between 1994 and 2006 included a Maple-derived algebra engine (MKM, aka Mathsoft Kernel Maple), though subsequent versions use MuPAD.
* Symbolic Math Toolbox in MATLAB
MATLAB (an abbreviation of "MATrix LABoratory") is a proprietary multi-paradigm programming language and numeric computing environment developed by MathWorks. MATLAB allows matrix manipulations, plotting of functions and data, implementa ...
contained a portion of the Maple 10 engine, but now uses MuPAD (starting with MATLAB R2007b+ release).
* Older versions of the mathematical editor Scientific Workplace included Maple as a computational engine, though current versions include MuPAD.
See also
* Comparison of computer algebra systems * Comparison of numerical-analysis software * Comparison of programming languages * Comparison of statistical packages * List of computer algebra systems * List of computer simulation software * List of graphing software * List of numerical-analysis software * Mathematical software * SageMath (an open source algebra program)References
External links
Maplesoft, division of Waterloo Maple, Inc.
– official website {{Authority control C (programming language) software Notebook interface Computer algebra system software for Linux Computer algebra system software for macOS Computer algebra system software for Windows Computer algebra systems Cross-platform software Data mining and machine learning software Data visualization software Data-centric programming languages Econometrics software Functional languages Interactive geometry software IRIX software Linear algebra Maplesoft Mathematical optimization software Mathematical software Numerical analysis software for Linux Numerical analysis software for macOS Numerical analysis software for Windows Numerical programming languages Numerical software Parallel computing Physics software Plotting software Products introduced in 1982 Proprietary commercial software for Linux Proprietary cross-platform software Regression and curve fitting software Simulation programming languages Software modeling language Statistical programming languages Theorem proving software systems Time series software