Macdonald's Constant Term Conjecture on:
[Wikipedia]
[Google]
[Amazon]
In mathematics, Macdonald polynomials ''P''λ(''x''; ''t'',''q'') are a family of
! .
Haiman's proof of the Macdonald positivity conjecture and the ''n''! conjecture involved showing that the
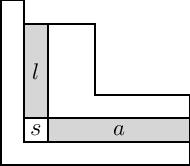 The transformed Macdonald polynomials in the formula above are related to the classical Macdonald polynomials via a sequence of transformations. First, the ''integral form'' of the Macdonald polynomials, denoted , is a re-scaling of that clears the denominators of the coefficients:
:
where is the collection of squares in the Young diagram of , and and denote the ''arm'' and ''leg'' of the square , as shown in the figure. ''Note: The figure at right uses French notation for tableau, which is flipped vertically from the English notation used on the Wikipedia page for Young diagrams. French notation is more commonly used in the study of Macdonald polynomials.''
The transformed Macdonald polynomials can then be defined in terms of the 's. We have
:
The transformed Macdonald polynomials in the formula above are related to the classical Macdonald polynomials via a sequence of transformations. First, the ''integral form'' of the Macdonald polynomials, denoted , is a re-scaling of that clears the denominators of the coefficients:
:
where is the collection of squares in the Young diagram of , and and denote the ''arm'' and ''leg'' of the square , as shown in the figure. ''Note: The figure at right uses French notation for tableau, which is flipped vertically from the English notation used on the Wikipedia page for Young diagrams. French notation is more commonly used in the study of Macdonald polynomials.''
The transformed Macdonald polynomials can then be defined in terms of the 's. We have
:
orthogonal
In mathematics, orthogonality is the generalization of the geometric notion of '' perpendicularity''.
By extension, orthogonality is also used to refer to the separation of specific features of a system. The term also has specialized meanings in ...
symmetric
Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definit ...
polynomials in several variables, introduced by Macdonald
Macdonald, MacDonald or McDonald may refer to:
Organisations
* McDonald's, a chain of fast food restaurants
* McDonald & Co., a former investment firm
* MacDonald Motorsports, a NASCAR team
* Macdonald Realty, a Canadian real estate brokerage f ...
in 1987. He later introduced a non-symmetric generalization in 1995. Macdonald originally associated his polynomials with weights λ of finite root systems and used just one variable ''t'', but later realized that it is more natural to associate them with affine root system
In mathematics, an affine root system is a root system of affine-linear functions on a Euclidean space. They are used in the classification of affine Lie algebra
In mathematics, a Lie algebra (pronounced ) is a vector space \mathfrak g to ...
s rather than finite root systems, in which case the variable ''t'' can be replaced by several different variables ''t''=(''t''1,...,''t''''k''), one for each of the ''k'' orbits of roots in the affine root system. The Macdonald polynomials are polynomials in ''n'' variables ''x''=(''x''1,...,''x''''n''), where ''n'' is the rank of the affine root system. They generalize many other families of orthogonal polynomials, such as Jack polynomial
In mathematics, the Jack function is a generalization of the Jack polynomial, introduced by Henry Jack. The Jack polynomial is a homogeneous, symmetric polynomial which generalizes the Schur and zonal polynomials, and is in turn generalized by ...
s and Hall–Littlewood polynomials and Askey–Wilson polynomials In mathematics, the Askey–Wilson polynomials (or ''q''-Wilson polynomials) are a family of orthogonal polynomials introduced by as q-analogs of the Wilson polynomials. They include many of the other orthogonal polynomials in 1 variable as specia ...
, which in turn include most of the named 1-variable orthogonal polynomials as special cases. Koornwinder polynomials
In mathematics, Macdonald-Koornwinder polynomials (also called Koornwinder polynomials) are a family of orthogonal polynomials in several variables, introduced by and I. G. Macdonald (1987, important special cases), that generalize the Askey–W ...
are Macdonald polynomials of certain non-reduced root systems. They have deep relationships with affine Hecke algebra
In mathematics, an affine Hecke algebra is the algebra associated to an affine Weyl group, and can be used to prove Macdonald's constant term conjecture for Macdonald polynomials.
Definition
Let V be a Euclidean space of a finite dimension and \S ...
s and Hilbert scheme
In algebraic geometry, a branch of mathematics, a Hilbert scheme is a scheme that is the parameter space for the closed subschemes of some projective space (or a more general projective scheme), refining the Chow variety. The Hilbert scheme is a d ...
s, which were used to prove several conjectures made by Macdonald about them.
Definition
First fix some notation: *''R'' is a finiteroot system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras, especially the classification and representat ...
in a real vector space ''V''.
*''R+'' is a choice of positive roots
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras, especially the classification and representatio ...
, to which corresponds a positive Weyl chamber
In mathematics, in particular the theory of Lie algebras, the Weyl group (named after Hermann Weyl) of a root system Φ is a subgroup of the isometry group of that root system. Specifically, it is the subgroup which is generated by reflections t ...
.
*''W'' is the Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group (named after Hermann Weyl) of a root system Φ is a subgroup of the isometry group of that root system. Specifically, it is the subgroup which is generated by reflections ...
of ''R''.
*''Q'' is the root lattice of ''R'' (the lattice spanned by the roots).
*''P'' is the weight lattice In the mathematical field of representation theory, a weight of an algebra ''A'' over a field F is an algebra homomorphism from ''A'' to F, or equivalently, a one-dimensional representation of ''A'' over F. It is the algebra analogue of a multipli ...
of ''R'' (containing ''Q'').
* An ordering on the weights: if and only if is a nonnegative linear combination of simple roots.
*''P+'' is the set of dominant weights: the elements of ''P'' in the positive Weyl chamber.
*ρ is the Weyl vector
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by . There is a closely related formula for the c ...
: half the sum of the positive roots; this is a special element of ''P''+ in the interior of the positive Weyl chamber.
*''F'' is a field of characteristic 0, usually the rational numbers.
*''A'' = ''F''(''P'') is the group algebra of ''P'', with a basis of elements written ''e''λ for λ ∈ ''P''.
* If ''f'' = ''e''λ, then ''f'' means ''e''−λ, and this is extended by linearity to the whole group algebra.
*''m''μ = Σλ ∈ ''W''μ''e''λ is an orbit sum; these elements form a basis for the subalgebra ''A''''W'' of elements fixed by ''W''.
*, the infinite q-Pochhammer symbol.
*
* is the inner product of two elements of ''A'', at least when ''t'' is a positive integer power of ''q''.
The Macdonald polynomials ''P''λ for λ ∈ ''P''+ are uniquely defined by the following two conditions:
: where ''u''λμ is a rational function of ''q'' and ''t'' with ''u''λλ = 1;
: ''P''λ and ''P''μ are orthogonal if λ < μ.
In other words, the Macdonald polynomials are obtained by orthogonalizing the obvious basis for ''A''''W''. The existence of polynomials with these properties is easy to show (for any inner product). A key property of the Macdonald polynomials is that they are orthogonal: 〈''P''λ, ''P''μ〉 = 0 whenever λ ≠ μ. This is not a trivial consequence of the definition because ''P''+ is not totally ordered, and so has plenty of elements that are incomparable. Thus one must check that the corresponding polynomials are still orthogonal. The orthogonality can be proved by showing that the Macdonald polynomials are eigenvectors
for an algebra of commuting self-adjoint operators with 1-dimensional eigenspaces, and using the fact that eigenspaces for different eigenvalues must be orthogonal.
In the case of non-simply-laced root systems (B, C, F, G), the parameter ''t'' can be chosen to vary with the length of the root, giving a three-parameter family of Macdonald polynomials. One can also extend the definition to the nonreduced root system BC, in which case one obtains a six-parameter family (one ''t'' for each orbit of roots, plus ''q'') known as Koornwinder polynomials
In mathematics, Macdonald-Koornwinder polynomials (also called Koornwinder polynomials) are a family of orthogonal polynomials in several variables, introduced by and I. G. Macdonald (1987, important special cases), that generalize the Askey–W ...
. It is sometimes better to regard Macdonald polynomials as depending on a possibly non-reduced affine root system. In this case, there is one parameter ''t'' associated to each orbit of roots in the affine root system, plus one parameter ''q''. The number of orbits of roots can vary from 1 to 5.
Examples
*If ''q'' = ''t'' the Macdonald polynomials become theWeyl character
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by . There is a closely related formula for the ch ...
s of the representations of the compact group of the root system, or the Schur functions in the case of root systems of type ''A''.
*If ''q'' = 0 the Macdonald polynomials become the (rescaled) zonal spherical function In mathematics, a zonal spherical function or often just spherical function is a function on a locally compact group ''G'' with compact subgroup ''K'' (often a maximal compact subgroup) that arises as the matrix coefficient of a ''K''-invariant vec ...
s for a semisimple ''p''-adic group, or the Hall–Littlewood polynomials In mathematics, the Hall–Littlewood polynomials are symmetric functions depending on a parameter ''t'' and a partition λ. They are Schur functions when ''t'' is 0 and monomial symmetric functions when ''t'' is 1 and are special cases of ...
when the root system has type ''A''.
*If ''t''=1 the Macdonald polynomials become the sums over ''W'' orbits, which are the monomial symmetric functions when the root system has type ''A''.
*If we put ''t'' = ''q''α and let ''q'' tend to 1 the Macdonald polynomials become Jack polynomial
In mathematics, the Jack function is a generalization of the Jack polynomial, introduced by Henry Jack. The Jack polynomial is a homogeneous, symmetric polynomial which generalizes the Schur and zonal polynomials, and is in turn generalized by ...
s when the root system is of type ''A'', and Heckman–Opdam polynomials In mathematics, Heckman–Opdam polynomials (sometimes called Jacobi polynomials) ''P''λ(''k'') are orthogonal polynomials in several variables associated to root systems. They were introduced by .
They generalize Jack polynomials when the roots ...
for more general root systems.
*For the affine root system ''A''1, the Macdonald polynomials are the Rogers polynomials.
*For the non-reduced rank 1 affine root system of type (''C'', ''C''1), the Macdonald polynomials are the Askey–Wilson polynomials In mathematics, the Askey–Wilson polynomials (or ''q''-Wilson polynomials) are a family of orthogonal polynomials introduced by as q-analogs of the Wilson polynomials. They include many of the other orthogonal polynomials in 1 variable as specia ...
, which in turn include as special cases most of the named families of orthogonal polynomials in 1 variable.
*For the non-reduced affine root system of type (''C'', ''C''''n''), the Macdonald polynomials are the Koornwinder polynomials
In mathematics, Macdonald-Koornwinder polynomials (also called Koornwinder polynomials) are a family of orthogonal polynomials in several variables, introduced by and I. G. Macdonald (1987, important special cases), that generalize the Askey–W ...
.
The Macdonald constant term conjecture
If ''t'' = ''q''''k'' for some positive integer ''k'', then the norm of the Macdonald polynomials is given by : This was conjectured by Macdonald (1982) as a generalization of theDyson conjecture
In mathematics, the Dyson conjecture is a conjecture about the constant term of certain Laurent polynomials, proved independently in 1962 by Wilson and Gunson. Andrews generalized it to the q-Dyson conjecture, proved by Zeilberger and Bressoud ...
, and proved for all (reduced) root systems by Cherednik (1995) using properties of double affine Hecke algebra In mathematics, a double affine Hecke algebra, or Cherednik algebra, is an algebra containing the Hecke algebra of an affine Weyl group, given as the quotient of the group ring of a double affine braid group. They were introduced by Cherednik, wh ...
s. The conjecture had previously been proved case-by-case for all roots systems except those of type ''E''''n'' by several authors.
There are two other conjectures which together with the norm conjecture are collectively referred to as the Macdonald conjectures in this context: in addition to the formula for the norm, Macdonald conjectured a formula for the value of ''P''λ at the point ''t''ρ, and a symmetry
:
Again, these were proved for general reduced root systems by , using double affine Hecke algebra In mathematics, a double affine Hecke algebra, or Cherednik algebra, is an algebra containing the Hecke algebra of an affine Weyl group, given as the quotient of the group ring of a double affine braid group. They were introduced by Cherednik, wh ...
s, with the extension to the BC case following shortly thereafter via work of van Diejen, Noumi, and Sahi.
The Macdonald positivity conjecture
In the case of roots systems of type ''A''''n''−1 the Macdonald polynomials are simply symmetric polynomials in ''n'' variables with coefficients that are rational functions of ''q'' and ''t''. A certain transformed version of the Macdonald polynomials (see Combinatorial formula below) form an orthogonal basis of the space of symmetric functions over , and therefore can be expressed in terms of Schur functions . The coefficients ''K''λμ(''q'',''t'') of these relations are called Kostka–Macdonald coefficients or ''qt''-Kostka coefficients. Macdonald conjectured that the Kostka–Macdonald coefficients were polynomials in ''q'' and ''t'' with non-negative integer coefficients. These conjectures are now proved; the hardest and final step was proving the positivity, which was done byMark Haiman
Mark David Haiman is a mathematician at the University of California at Berkeley who proved the
Macdonald positivity conjecture for Macdonald polynomials. He received his Ph.D in 1984 in the Massachusetts Institute of Technology under the directio ...
(2001), by proving the ''n''! conjecture.
It is still a central open problem in algebraic combinatorics to find a combinatorial formula for the ''qt''-Kostka coefficients.
n! conjecture
The ''n''! conjecture ofAdriano Garsia
Adriano Mario Garsia (born 20 August 1928) is a Tunisian-born Italian American mathematician who works in analysis, combinatorics, representation theory, and algebraic geometry. He is a student of Charles Loewner and has published work on represe ...
and Mark Haiman
Mark David Haiman is a mathematician at the University of California at Berkeley who proved the
Macdonald positivity conjecture for Macdonald polynomials. He received his Ph.D in 1984 in the Massachusetts Institute of Technology under the directio ...
states that for each partition μ of ''n'' the space
:
spanned by all higher partial derivatives of
:
has dimension ''n''!, where (''p''''j'', ''q''''j'') run through the ''n'' elements of the diagram of the partition μ, regarded as a subset of the pairs of non-negative integers.
For example, if μ is the partition 3 = 2 + 1 of ''n'' = 3 then the pairs (''p''''j'', ''q''''j'') are
(0, 0), (0, 1), (1, 0), and the space ''D''μ is spanned by
:
:
:
:
:
:
which has dimension 6 = 3isospectral Hilbert scheme
In mathematics, two linear operators are called isospectral or cospectral if they have the same spectrum. Roughly speaking, they are supposed to have the same sets of eigenvalues, when those are counted with multiplicity.
The theory of isospect ...
of ''n'' points in a plane was Cohen–Macaulay (and even Gorenstein Gorenstein may refer to:
* Daniel Gorenstein (1923–1992), American mathematician, known for
**Alperin–Brauer–Gorenstein theorem
**Gorenstein–Harada theorem
**Gorenstein ring
**Gorenstein scheme
**Gorenstein–Walter theorem
* Eli Gorenstein ...
). Earlier results of Haiman and Garsia had already shown that this implied the ''n''! conjecture, and that the ''n''! conjecture implied that the Kostka–Macdonald coefficients were graded character multiplicities for the modules ''D''μ. This immediately implies the Macdonald positivity conjecture because character multiplicities have to be non-negative integers.
Ian Grojnowski and Mark Haiman found another proof of the Macdonald positivity conjecture by proving a positivity conjecture for LLT polynomial
In mathematics, an LLT polynomial is one of a family of symmetric functions introduced by Alain Lascoux, Bernard Leclerc, and Jean-Yves Thibon (1997) as ''q''-analogues of products of Schur functions.
J. Haglund, M. Haiman, N. Loehr (2005) showe ...
s.
Combinatorial formula for the Macdonald polynomials
In 2005, J. Haglund, M. Haiman and N. Loehr gave the first proof of a combinatorial interpretation of the Macdonald polynomials. In 1988, I.G. Macdonald gave the second proof of a combinatorial interpretation of the Macdonald polynomials (equations (4.11) and (5.13)). Macdonald’s formula is different to that in Haglund, Haiman, and Loehr's work, with many fewer terms (this formula is proved also in Macdonald's seminal work, Ch. VI (7.13)). While very useful for computation and interesting in its own right, their combinatorial formulas do not immediately imply positivity of the Kostka-Macdonald coefficients as the give the decomposition of the Macdonald polynomials into monomial symmetric functions rather than into Schur functions. Written in the ''transformed Macdonald polynomials'' rather than the usual , they are : where σ is a filling of theYoung diagram In mathematics, a Young tableau (; plural: tableaux) is a combinatorial object useful in representation theory and Schubert calculus. It provides a convenient way to describe the group representations of the symmetric and general linear groups ...
of shape μ, ''inv'' and ''maj'' are certain combinatorial statistics (functions) defined on the filling σ. This formula expresses the Macdonald polynomials in infinitely many variables. To obtain the polynomials in ''n'' variables, simply restrict the formula to fillings that only use the integers 1, 2, ..., ''n''. The term ''x''σ should be interpreted as where ''σi'' is the number of boxes in the filling of μ with content ''i''.
 The transformed Macdonald polynomials in the formula above are related to the classical Macdonald polynomials via a sequence of transformations. First, the ''integral form'' of the Macdonald polynomials, denoted , is a re-scaling of that clears the denominators of the coefficients:
:
where is the collection of squares in the Young diagram of , and and denote the ''arm'' and ''leg'' of the square , as shown in the figure. ''Note: The figure at right uses French notation for tableau, which is flipped vertically from the English notation used on the Wikipedia page for Young diagrams. French notation is more commonly used in the study of Macdonald polynomials.''
The transformed Macdonald polynomials can then be defined in terms of the 's. We have
:
The transformed Macdonald polynomials in the formula above are related to the classical Macdonald polynomials via a sequence of transformations. First, the ''integral form'' of the Macdonald polynomials, denoted , is a re-scaling of that clears the denominators of the coefficients:
:
where is the collection of squares in the Young diagram of , and and denote the ''arm'' and ''leg'' of the square , as shown in the figure. ''Note: The figure at right uses French notation for tableau, which is flipped vertically from the English notation used on the Wikipedia page for Young diagrams. French notation is more commonly used in the study of Macdonald polynomials.''
The transformed Macdonald polynomials can then be defined in terms of the 's. We have
: