Lowest Landau Level on:
[Wikipedia]
[Google]
[Amazon]
In
 Consider a system of non-interacting particles with charge and spin confined to an area in the plane. Apply a uniform magnetic field along the -axis. In CGS units, the
Consider a system of non-interacting particles with charge and spin confined to an area in the plane. Apply a uniform magnetic field along the -axis. In CGS units, the
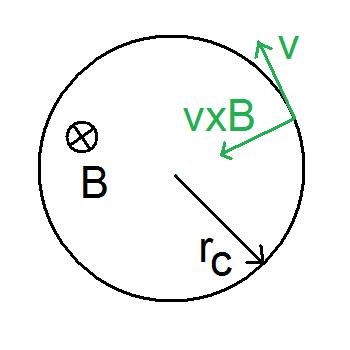
 An electron following
An electron following
quantum mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, ...
, Landau quantization refers to the quantization of the cyclotron orbits of charged particles in a uniform magnetic field. As a result, the charged particles can only occupy orbits with discrete, equidistant energy values, called Landau levels. These levels are degenerate
Degeneracy, degenerate, or degeneration may refer to:
Arts and entertainment
* Degenerate (album), ''Degenerate'' (album), a 2010 album by the British band Trigger the Bloodshed
* Degenerate art, a term adopted in the 1920s by the Nazi Party i ...
, with the number of electrons per level directly proportional to the strength of the applied magnetic field. It is named after the Soviet physicist Lev Landau
Lev Davidovich Landau (russian: Лев Дави́дович Ланда́у; 22 January 1908 – 1 April 1968) was a Soviet- Azerbaijani physicist of Jewish descent who made fundamental contributions to many areas of theoretical physics.
His a ...
.
Landau quantization is directly responsible for the electronic susceptibility of metals, known as Landau diamagnetism
Diamagnetic materials are repelled by a magnetic field; an applied magnetic field creates an induced magnetic field in them in the opposite direction, causing a repulsive force. In contrast, paramagnetic and ferromagnetic materials are attract ...
. Under strong magnetic fields, Landau quantization leads to oscillations in electronic properties of materials as a function of the applied magnetic field known as De Haas–Van Alphen and Shubnikov–de Haas effects.
Landau quantization is a key ingredient to explain the integer quantum Hall effect.
Derivation
 Consider a system of non-interacting particles with charge and spin confined to an area in the plane. Apply a uniform magnetic field along the -axis. In CGS units, the
Consider a system of non-interacting particles with charge and spin confined to an area in the plane. Apply a uniform magnetic field along the -axis. In CGS units, the Hamiltonian
Hamiltonian may refer to:
* Hamiltonian mechanics, a function that represents the total energy of a system
* Hamiltonian (quantum mechanics), an operator corresponding to the total energy of that system
** Dyall Hamiltonian, a modified Hamiltonian ...
of this system (here, the effects of spin are neglected) is
Here, is the canonical
The adjective canonical is applied in many contexts to mean "according to the canon" the standard, rule or primary source that is accepted as authoritative for the body of knowledge or literature in that context. In mathematics, "canonical example ...
momentum operator
In quantum mechanics, the momentum operator is the operator (physics), operator associated with the momentum (physics), linear momentum. The momentum operator is, in the position representation, an example of a differential operator. For the case o ...
and is the electromagnetic vector potential, which is related to the magnetic field
A magnetic field is a vector field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular to its own velocity and to ...
by
There is some gauge freedom in the choice of vector potential for a given magnetic field. The Hamiltonian is gauge invariant
In physics, a gauge theory is a type of field theory in which the Lagrangian (and hence the dynamics of the system itself) does not change (is invariant) under local transformations according to certain smooth families of operations (Lie groups) ...
, which means that adding the gradient of a scalar field
In mathematics and physics, a scalar field is a function (mathematics), function associating a single number to every point (geometry), point in a space (mathematics), space – possibly physical space. The scalar may either be a pure Scalar ( ...
to changes the overall phase of the wave function
A wave function in quantum physics is a mathematical description of the quantum state of an isolated quantum system. The wave function is a complex-valued probability amplitude, and the probabilities for the possible results of measurements mad ...
by an amount corresponding to the scalar field. But physical properties are not influenced by the specific choice of gauge.
In the Landau gauge
For simplicity in calculation, choose theLandau gauge
In the physics of gauge theories, gauge fixing (also called choosing a gauge) denotes a mathematical procedure for coping with redundant degrees of freedom in field variables. By definition, a gauge theory represents each physically distinct co ...
, which is
where and is the component of the position operator.
In this gauge, the Hamiltonian is
The operator commutes with this Hamiltonian, since the operator is absent by the choice of gauge. Thus the operator can be replaced by its eigenvalue . Since does not appear in the Hamiltonian and only the z-momentum appears in the kinetic energy, this motion along the z-direction is a free motion.
The Hamiltonian can also be written more simply by noting that the cyclotron frequency
Cyclotron resonance describes the interaction of external forces with charged particles experiencing a magnetic field, thus already moving on a circular path. It is named after the cyclotron, a cyclic particle accelerator that utilizes an oscillati ...
is , giving
This is exactly the Hamiltonian for the quantum harmonic oscillator
量子調和振動子 は、 古典調和振動子 の 量子力学 類似物です。任意の滑らかな ポテンシャル は通常、安定した 平衡点 の近くで 調和ポテンシャル として近似できるため、最� ...
, except with the minimum of the potential shifted in coordinate space by .
To find the energies, note that translating the harmonic oscillator potential does not affect the energies. The energies of this system are thus identical to those of the standard quantum harmonic oscillator
量子調和振動子 は、 古典調和振動子 の 量子力学 類似物です。任意の滑らかな ポテンシャル は通常、安定した 平衡点 の近くで 調和ポテンシャル として近似できるため、最� ...
,
The energy does not depend on the quantum number , so there will be a finite number of degeneracies (If the particle is placed in an unconfined space, this degeneracy will correspond to a continuous sequence of ). The value of is continuous if the particle is unconfined in the z-direction and discrete if the particle is bounded in the z-direction also. Each set of wave functions with the same value of is called a Landau level.
For the wave functions, recall that commutes with the Hamiltonian. Then the wave function factors into a product of momentum eigenstates in the direction and harmonic oscillator eigenstates shifted by an amount 0 in the direction:
where . In sum, the state of the electron is characterized by the quantum numbers, , and .
In the symmetric gauge
The derivation treated and ''y'' as slightly asymmetric. However, by the symmetry of the system, there is no physical quantity which distinguishes these coordinates. The same result could have been obtained with an appropriate interchange of and . A more adequate choice of gauge, is the symmetric gauge, which refers to the choice In terms of dimensionless lengths and energies, the Hamiltonian can be expressed as The correct units can be restored by introducing factors of and . Consider operators These operators follow certain commutation relations In terms of above operators the Hamiltonian can be written as where we reintroduced the units back. The Landau level index is the eigenvalue of the operator . The application of increases by one unit while preserving , whereas application simultaneously increase and decreases by one unit. The analogy toquantum harmonic oscillator
量子調和振動子 は、 古典調和振動子 の 量子力学 類似物です。任意の滑らかな ポテンシャル は通常、安定した 平衡点 の近くで 調和ポテンシャル として近似できるため、最� ...
provides solutions
where
and
One may verify that the above states correspond to choosing wavefunctions proportional to
where .
In particular, the lowest Landau level consists of arbitrary analytic functions multiplying a Gaussian, .
Degeneracy of the Landau levels
In the Landau gauge
The effects of Landau levels may only be observed when the mean thermal energy is smaller than the energy level separation, , meaning low temperatures and strong magnetic fields. Each Landau level is degenerate because of the second quantum number , which can take the values where is an integer. The allowed values of are further restricted by the condition that the center of force of the oscillator, , must physically lie within the system, . This gives the following range for , For particles with charge , the upper bound on can be simply written as a ratio of fluxes, where is the fundamentalmagnetic flux quantum
The magnetic flux, represented by the symbol , threading some contour or loop is defined as the magnetic field multiplied by the loop area , i.e. . Both and can be arbitrary, meaning can be as well. However, if one deals with the superconducti ...
and is the flux through the system (with area ).
Thus, for particles with spin , the maximum number of particles per Landau level is
which for electrons (where and ) gives , two available states for each flux quantum that penetrates the system.
The above gives only a rough idea of the effects of finite-size geometry. Strictly speaking, using the standard solution of the harmonic oscillator is only valid for systems unbounded in the -direction (infinite strips). If the size is finite, boundary conditions in that direction give rise to non-standard quantization conditions on the magnetic field, involving (in principle) both solutions to the Hermite equation. The filling of these levels with many electrons is still an active area of research.
In general, Landau levels are observed in electronic systems. As the magnetic field is increased, more and more electrons can fit into a given Landau level. The occupation of the highest Landau level ranges from completely full to entirely empty, leading to oscillations in various electronic properties (see De Haas–Van Alphen effect and Shubnikov–de Haas effect An oscillation in the conductivity of a material that occurs at low temperatures in the presence of very intense magnetic fields, the Shubnikov–de Haas effect (SdH) is a macroscopic manifestation of the inherent quantum mechanical nature of matter ...
).
If Zeeman splitting
The Zeeman effect (; ) is the effect of splitting of a spectral line into several components in the presence of a static magnetic field. It is named after the Dutch physicist Pieter Zeeman, who discovered it in 1896 and received a Nobel prize ...
is included, each Landau level splits into a pair, one for spin up electrons and the other for spin down electrons. Then the occupation of each spin Landau level is just the ratio of fluxes . Zeeman splitting has a significant effect on the Landau levels because their energy scales are the same, . However, the Fermi energy and ground state energy stay roughly the same in a system with many filled levels, since pairs of split energy levels cancel each other out when summed.
Moreover, the above derivation in the Landau gauge assumed an electron confined in the -direction, which is a relevant experimental situation — found in two-dimensional electron gases, for instance. Still, this assumption is not essential for the results. If electrons are free to move along the direction, the wave function acquires an additional multiplicative term ; the energy corresponding to this free motion, , is added to the discussed. This term then fills in the separation in energy of the different Landau levels, blurring the effect of the quantization. Nevertheless, the motion in the --plane, perpendicular to the magnetic field, is still quantized.
In the symmetric gauge
Each Landau level has degenerate orbitals labeled by the quantum numbers in symmetric gauge. The degeneracy per unit area is the same in each Landau level. The ''z'' component of angular momentum is Exploiting the property we chose eigenfunctions which diagonalize and , The eigenvalue of is denoted by , where it is clear that in the th Landau level. However, it may be arbitrarily large, which is necessary to obtain the infinite degeneracy (or finite degeneracy per unit area) exhibited by the system.Relativistic case
Dirac equation
In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin- massive particles, called "Dirac part ...
under a constant magnetic field, can be analytically solved. The energies are given by
where ''c'' is the speed of light, the sign depends on the particle-antiparticle component and ''ν'' is a non-negative integer. Due to spin, all levels are degenerate except for the ground state at .
The massless 2D case can be simulated in single-layer materials
In materials science, the term single-layer materials or 2D materials refers to crystalline solids consisting of a single layer of atoms. These materials are promising for some applications but remain the focus of research. Single-layer materials ...
like graphene
Graphene () is an allotrope of carbon consisting of a single layer of atoms arranged in a hexagonal lattice nanostructure.
near the Dirac cone, Dirac cones, where the eigenergies are given by
where the speed of light has to be replaced with the Fermi speed ''v''F of the material and the minus sign corresponds to electron hole
In physics, chemistry, and electronic engineering, an electron hole (often simply called a hole) is a quasiparticle which is the lack of an electron at a position where one could exist in an atom or atomic lattice. Since in a normal atom or ...
s.
Magnetic susceptibility of a Fermi gas
TheFermi gas
An ideal Fermi gas is a state of matter which is an ensemble of many non-interacting fermions. Fermions are particles that obey Fermi–Dirac statistics, like electrons, protons, and neutrons, and, in general, particles with half-integer spin. ...
(an ensemble of non-interacting fermion
In particle physics, a fermion is a particle that follows Fermi–Dirac statistics. Generally, it has a half-odd-integer spin: spin , spin , etc. In addition, these particles obey the Pauli exclusion principle. Fermions include all quarks an ...
s) is part of the basis for understanding of the thermodynamic properties of metals. In 1930 Landau derived an estimate for the magnetic susceptibility
In electromagnetism, the magnetic susceptibility (Latin: , "receptive"; denoted ) is a measure of how much a material will become magnetized in an applied magnetic field. It is the ratio of magnetization (magnetic moment per unit volume) to the ap ...
of a Fermi gas, known as Landau susceptibility, which is constant for small magnetic fields. Landau also noticed that the susceptibility oscillates with high frequency for large magnetic fields, this physical phenomenon is known as the De Haas–Van Alphen effect.
Two-dimensional lattice
Thetight binding
In solid-state physics, the tight-binding model (or TB model) is an approach to the calculation of electronic band structure using an approximate set of wave functions based upon superposition of wave functions for isolated atoms located at each ...
energy spectrum of charged particles in a two dimensional infinite lattice is known to be self-similar
__NOTOC__
In mathematics, a self-similar object is exactly or approximately similar to a part of itself (i.e., the whole has the same shape as one or more of the parts). Many objects in the real world, such as coastlines, are statistically se ...
and fractal
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illu ...
, as demonstrated in Hofstadter's butterfly
In condensed matter physics, Hofstadter's butterfly is a graph of the spectral properties of non-interacting two-dimensional electrons in a perpendicular magnetic field in a lattice. The fractal, self-similar nature of the spectrum was discovered ...
. For an integer ratio of the magnetic flux quantum
The magnetic flux, represented by the symbol , threading some contour or loop is defined as the magnetic field multiplied by the loop area , i.e. . Both and can be arbitrary, meaning can be as well. However, if one deals with the superconducti ...
and the magnetic flux through a lattice cell, one recovers the Landau levels for large integers.
Integer quantum Hall effect
See also
*Barkhausen effect
The Barkhausen effect is a name given to the noise in the magnetic output of a ferromagnet when the magnetizing force applied to it is changed. Discovered by German physicist Heinrich Barkhausen in 1919, it is caused by rapid changes of size o ...
*Laughlin wavefunction In condensed matter physics, the Laughlin wavefunction pp. 210-213 is an ansatz, proposed by Robert Laughlin for the ground state of a two-dimensional electron gas placed in a uniform background magnetic field in the presence of a uniform jellium ...
*Static forces and virtual-particle exchange
Static force fields are fields, such as a simple Electric field, electric, Magnetic field, magnetic or gravitational fields, that exist without excitations. The Perturbation theory (quantum mechanics), most common approximation method that physici ...
References
Further reading
* Landau, L. D.; and Lifschitz, E. M.; (1977). ''Quantum Mechanics: Non-relativistic Theory. Course of Theoretical Physics''. Vol. 3 (3rd ed. London: Pergamon Press). {{ISBN, 0750635398. Quantum mechanics Electric and magnetic fields in matter Lev Landau