Lie sphere geometry on:
[Wikipedia]
[Google]
[Amazon]
 Lie sphere geometry is a
Lie sphere geometry is a
 The projective space RP4 is the space of lines through the
The projective space RP4 is the space of lines through the
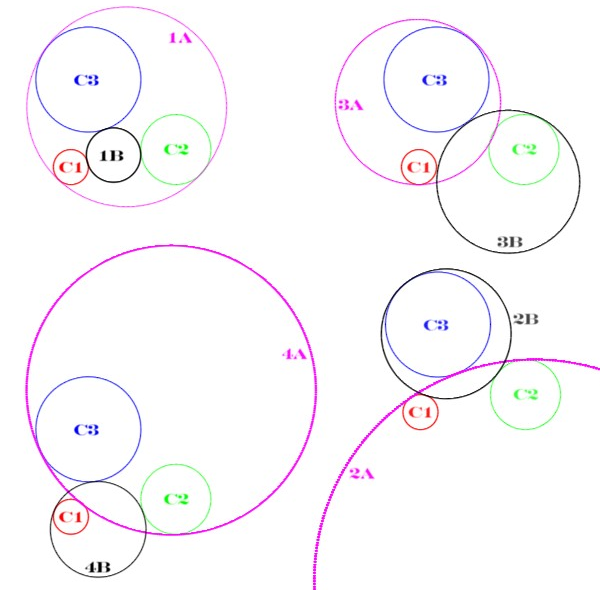 The incidence of cycles in Lie sphere geometry provides a simple solution to the problem of Apollonius. This problem concerns a configuration of three distinct circles (which may be points or lines): the aim is to find every other circle (including points or lines) which is tangent to all three of the original circles. For a generic configuration of circles, there are at most eight such tangent circles.
The solution, using Lie sphere geometry, proceeds as follows. Choose an orientation for each of the three circles (there are eight ways to do this, but there are only four up to reversing the orientation of all three). This defines three points ''x ''y ''zon the Lie quadric ''Q''. By the incidence of cycles, a solution to the Apollonian problem compatible with the chosen orientations is given by a point ''q∈ ''Q'' such that q is orthogonal to x, y and z. If these three vectors are linearly dependent, then the corresponding points ''x ''y ''zlie on a line in projective space. Since a nontrivial quadratic equation has at most two solutions, this line actually lies in the Lie quadric, and any point ''qon this line defines a cycle incident with ''x ''yand ''z Thus there are infinitely many solutions in this case.
If instead x, y and z are linearly independent then the subspace ''V'' orthogonal to all three is 2-dimensional. It can have signature (2,0), (1,0), or (1,1), in which case there are zero, one or two solutions for ''qrespectively. (The signature cannot be (0,1) or (0,2) because it is orthogonal to a space containing more than one null line.) In the case that the subspace has signature (1,0), the unique solution q lies in the span of x, y and z.
The general solution to the Apollonian problem is obtained by reversing orientations of some of the circles, or equivalently, by considering the triples (x,''ρ''(y),z), (x,y,''ρ''(z)) and (x,''ρ''(y),''ρ''(z)).
Note that the triple (''ρ''(x),''ρ''(y),''ρ''(z)) yields the same solutions as (x,y,z), but with an overall reversal of orientation. Thus there are at most 8 solution circles to the Apollonian problem unless all three circles meet tangentially at a single point, when there are infinitely many solutions.
The incidence of cycles in Lie sphere geometry provides a simple solution to the problem of Apollonius. This problem concerns a configuration of three distinct circles (which may be points or lines): the aim is to find every other circle (including points or lines) which is tangent to all three of the original circles. For a generic configuration of circles, there are at most eight such tangent circles.
The solution, using Lie sphere geometry, proceeds as follows. Choose an orientation for each of the three circles (there are eight ways to do this, but there are only four up to reversing the orientation of all three). This defines three points ''x ''y ''zon the Lie quadric ''Q''. By the incidence of cycles, a solution to the Apollonian problem compatible with the chosen orientations is given by a point ''q∈ ''Q'' such that q is orthogonal to x, y and z. If these three vectors are linearly dependent, then the corresponding points ''x ''y ''zlie on a line in projective space. Since a nontrivial quadratic equation has at most two solutions, this line actually lies in the Lie quadric, and any point ''qon this line defines a cycle incident with ''x ''yand ''z Thus there are infinitely many solutions in this case.
If instead x, y and z are linearly independent then the subspace ''V'' orthogonal to all three is 2-dimensional. It can have signature (2,0), (1,0), or (1,1), in which case there are zero, one or two solutions for ''qrespectively. (The signature cannot be (0,1) or (0,2) because it is orthogonal to a space containing more than one null line.) In the case that the subspace has signature (1,0), the unique solution q lies in the span of x, y and z.
The general solution to the Apollonian problem is obtained by reversing orientations of some of the circles, or equivalently, by considering the triples (x,''ρ''(y),z), (x,y,''ρ''(z)) and (x,''ρ''(y),''ρ''(z)).
Note that the triple (''ρ''(x),''ρ''(y),''ρ''(z)) yields the same solutions as (x,y,z), but with an overall reversal of orientation. Thus there are at most 8 solution circles to the Apollonian problem unless all three circles meet tangentially at a single point, when there are infinitely many solutions.
 Lie sphere geometry provides a natural description of Dupin cyclides. These are characterized as the common envelope of two one parameter families of spheres ''S''(''s'') and ''T''(''t''), where ''S'' and ''T'' are maps from intervals into the Lie quadric. In order for a common envelope to exist, ''S''(''s'') and ''T''(''t'') must be incident for all ''s'' and ''t'', i.e., their representative vectors must span a null 2-dimensional subspace of R4,2. Hence they define a map into the space of contact elements Z5. This map is Legendrian if and only if the derivatives of ''S'' (or ''T'') are orthogonal to ''T'' (or ''S''), i.e., if and only if there is an orthogonal decomposition of R4,2 into a direct sum of 3-dimensional subspaces ''σ'' and ''τ'' of signature (2,1), such that ''S'' takes values in ''σ'' and ''T'' takes values in ''τ''. Conversely such a decomposition uniquely determines a contact lift of a surface which envelops two one parameter families of spheres; the image of this contact lift is given by the null 2-dimensional subspaces which intersect ''σ'' and ''τ'' in a pair of null lines.
Such a decomposition is equivalently given, up to a sign choice, by a symmetric endomorphism of R4,2 whose square is the identity and whose ±1 eigenspaces are ''σ'' and ''τ''. Using the inner product on R4,2, this is determined by a quadratic form on R4,2.
To summarize, Dupin cyclides are determined by quadratic forms on R4,2 such that the associated symmetric endomorphism has square equal to the identity and eigenspaces of signature (2,1).
This provides one way to see that Dupin cyclides are cyclides, in the sense that they are zero-sets of quartics of a particular form. For this, note that as in the planar case, 3-dimensional Euclidean space embeds into the Lie quadric ''Q''3 as the set of point spheres apart from the ideal point at infinity. Explicitly, the point (x,y,z) in Euclidean space corresponds to the point
: , ''x'', ''y'', ''z'', –1, (''x''2 + ''y''2 + ''z''2)/2in ''Q''3. A cyclide consists of the points ,''x''1,''x''2,''x''3,''x''4,''x''5∈ ''Q''3 which satisfy an additional quadratic relation
:
for some symmetric 5 ×; 5 matrix ''A'' = (''a''''ij''). The class of cyclides is a natural family of surfaces in Lie sphere geometry, and the Dupin cyclides form a natural subfamily.
Lie sphere geometry provides a natural description of Dupin cyclides. These are characterized as the common envelope of two one parameter families of spheres ''S''(''s'') and ''T''(''t''), where ''S'' and ''T'' are maps from intervals into the Lie quadric. In order for a common envelope to exist, ''S''(''s'') and ''T''(''t'') must be incident for all ''s'' and ''t'', i.e., their representative vectors must span a null 2-dimensional subspace of R4,2. Hence they define a map into the space of contact elements Z5. This map is Legendrian if and only if the derivatives of ''S'' (or ''T'') are orthogonal to ''T'' (or ''S''), i.e., if and only if there is an orthogonal decomposition of R4,2 into a direct sum of 3-dimensional subspaces ''σ'' and ''τ'' of signature (2,1), such that ''S'' takes values in ''σ'' and ''T'' takes values in ''τ''. Conversely such a decomposition uniquely determines a contact lift of a surface which envelops two one parameter families of spheres; the image of this contact lift is given by the null 2-dimensional subspaces which intersect ''σ'' and ''τ'' in a pair of null lines.
Such a decomposition is equivalently given, up to a sign choice, by a symmetric endomorphism of R4,2 whose square is the identity and whose ±1 eigenspaces are ''σ'' and ''τ''. Using the inner product on R4,2, this is determined by a quadratic form on R4,2.
To summarize, Dupin cyclides are determined by quadratic forms on R4,2 such that the associated symmetric endomorphism has square equal to the identity and eigenspaces of signature (2,1).
This provides one way to see that Dupin cyclides are cyclides, in the sense that they are zero-sets of quartics of a particular form. For this, note that as in the planar case, 3-dimensional Euclidean space embeds into the Lie quadric ''Q''3 as the set of point spheres apart from the ideal point at infinity. Explicitly, the point (x,y,z) in Euclidean space corresponds to the point
: , ''x'', ''y'', ''z'', –1, (''x''2 + ''y''2 + ''z''2)/2in ''Q''3. A cyclide consists of the points ,''x''1,''x''2,''x''3,''x''4,''x''5∈ ''Q''3 which satisfy an additional quadratic relation
:
for some symmetric 5 ×; 5 matrix ''A'' = (''a''''ij''). The class of cyclides is a natural family of surfaces in Lie sphere geometry, and the Dupin cyclides form a natural subfamily.
"On complexes - in particular, line and sphere complexes - with applications to the theory of partial differential equations"
English translation of Lie's key paper on the subject
"Oriented circles and 3D relativistic geometry"
An elementary video introducing concepts in Laguerre geometry (whose transformation group is a subgroup of the group of Lie transformations). The video is presented from the
 Lie sphere geometry is a
Lie sphere geometry is a geometrical
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is ca ...
theory of planar or spatial geometry
Three-dimensional space (also: 3D space, 3-space or, rarely, tri-dimensional space) is a geometric setting in which three values (called ''parameters'') are required to determine the position (geometry), position of an element (i.e., Point (m ...
in which the fundamental concept is the circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is const ...
or sphere
A sphere () is a Geometry, geometrical object that is a solid geometry, three-dimensional analogue to a two-dimensional circle. A sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three ...
. It was introduced by Sophus Lie
Marius Sophus Lie ( ; ; 17 December 1842 – 18 February 1899) was a Norwegian mathematician. He largely created the theory of continuous symmetry and applied it to the study of geometry and differential equations.
Life and career
Marius Sophu ...
in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.
The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a n ...
known as the Lie quadric
Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is tha ...
(a quadric hypersurface in projective space
In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seem to meet ''at infinity''. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally ...
). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).
To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.
Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric
In mathematics, the lines of a 3-dimensional projective space, ''S'', can be viewed as points of a 5-dimensional projective space, ''T''. In that 5-space, the points that represent each line in ''S'' lie on a quadric, ''Q'' known as the Klein q ...
. This similarity led Lie to his famous "line-sphere correspondence" between the space of lines and the space of spheres in 3-dimensional space.Lie was particularly pleased with this achievement: see .
Basic concepts
The key observation that leads to Lie sphere geometry is that theorems of Euclidean geometry in the plane (resp. in space) which only depend on the concepts of circles (resp. spheres) and theirtangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More ...
ial contact
Contact may refer to:
Interaction Physical interaction
* Contact (geology), a common geological feature
* Contact lens or contact, a lens placed on the eye
* Contact sport, a sport in which players make contact with other players or objects
* ...
have a more natural formulation in a more general context in which circles, line
Line most often refers to:
* Line (geometry), object with zero thickness and curvature that stretches to infinity
* Telephone line, a single-user circuit on a telephone communication system
Line, lines, The Line, or LINE may also refer to:
Arts ...
s and points
Point or points may refer to:
Places
* Point, Lewis, a peninsula in the Outer Hebrides, Scotland
* Point, Texas, a city in Rains County, Texas, United States
* Point, the NE tip and a ferry terminal of Lismore, Inner Hebrides, Scotland
* Point ...
(resp. spheres, planes
Plane(s) most often refers to:
* Aero- or airplane, a powered, fixed-wing aircraft
* Plane (geometry), a flat, 2-dimensional surface
Plane or planes may also refer to:
Biology
* Plane (tree) or ''Platanus'', wetland native plant
* ''Planes' ...
and points) are treated on an equal footing. This is achieved in three steps. First an ideal point at infinity
In geometry, a point at infinity or ideal point is an idealized limiting point at the "end" of each line.
In the case of an affine plane (including the Euclidean plane), there is one ideal point for each pencil of parallel lines of the plane. Adj ...
is added to Euclidean space so that lines (or planes) can be regarded as circles (or spheres) passing through the point at infinity (i.e., having infinite radius
In classical geometry, a radius ( : radii) of a circle or sphere is any of the line segments from its center to its perimeter, and in more modern usage, it is also their length. The name comes from the latin ''radius'', meaning ray but also the ...
). This extension is known as inversive geometry
Inversive activities are processes which self internalise the action concerned. For example, a person who has an Inversive personality internalises his emotions from any exterior source. An inversive heat source would be a heat source where all th ...
with automorphisms known as "Mobius transformations". Second, points are regarded as circles (or spheres) of zero radius. Finally, for technical reasons, the circles (or spheres), including the lines (or planes) are given orientations.
These objects, i.e., the points, oriented circles and oriented lines in the plane, or the points, oriented spheres and oriented planes in space, are sometimes called cycles or Lie cycles. It turns out that they form a quadric hypersurface in a projective space
In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seem to meet ''at infinity''. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally ...
of dimension 4 or 5, which is known as the Lie quadric. The natural symmetries
Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definiti ...
of this quadric form a group of transformations known as the Lie transformations. These transformations do not preserve points in general: they are transforms of the Lie quadric, ''not'' of the plane/sphere plus point at infinity. The point-preserving transformations are precisely the Möbius transformations. The Lie transformations which fix the ideal point at infinity are the Laguerre transformations
Edmond Nicolas Laguerre (9 April 1834, Bar-le-Duc – 14 August 1886, Bar-le-Duc) was a French mathematician and a member of the Académie des sciences (1885). His main works were in the areas of geometry and complex analysis. He also investigat ...
of Laguerre geometry
Edmond Nicolas Laguerre (9 April 1834, Bar-le-Duc – 14 August 1886, Bar-le-Duc) was a French mathematician and a member of the Académie des sciences (1885). His main works were in the areas of geometry and complex analysis. He also investigate ...
. These two subgroups generate the group of Lie transformations, and their intersection are the Möbius transforms that fix the ideal point at infinity, namely the affine conformal maps.
These groups also have a direct physical interpretation: As pointed out by Harry Bateman
Harry Bateman FRS (29 May 1882 – 21 January 1946) was an English mathematician with a specialty in differential equations of mathematical physics. With Ebenezer Cunningham, he expanded the views of spacetime symmetry of Lorentz and Poincare ...
, the Lie sphere transformations are identical with the spherical wave transformation
Spherical wave transformations leave the form of spherical waves as well as the laws of optics and electrodynamics invariant in all inertial frames. They were defined between 1908 and 1909 by Harry Bateman and Ebenezer Cunningham, with Bateman givi ...
s that leave the form of Maxwell's equations
Maxwell's equations, or Maxwell–Heaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, and electric circuits.
...
invariant. In addition, Élie Cartan
Élie Joseph Cartan (; 9 April 1869 – 6 May 1951) was an influential French mathematician who did fundamental work in the theory of Lie groups, differential systems (coordinate-free geometric formulation of PDEs), and differential geometry. ...
, Henri Poincaré
Jules Henri Poincaré ( S: stress final syllable ; 29 April 1854 – 17 July 1912) was a French mathematician, theoretical physicist, engineer, and philosopher of science. He is often described as a polymath, and in mathematics as "The ...
and Wilhelm Blaschke pointed out that the Laguerre group is simply isomorphic to the Lorentz group of special relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory regarding the relationship between space and time. In Albert Einstein's original treatment, the theory is based on two postulates:
# The laws o ...
(see Laguerre group isomorphic to Lorentz group). Eventually, there is also an isomorphism between the Möbius group and the Lorentz group (see Möbius group#Lorentz transformation).
Lie sphere geometry in the plane
The Lie quadric
The Lie quadric of the plane is defined as follows. Let R3,2 denote the space R5 of 5-tuples of real numbers, equipped with thesignature
A signature (; from la, signare, "to sign") is a handwritten (and often stylized) depiction of someone's name, nickname, or even a simple "X" or other mark that a person writes on documents as a proof of identity and intent. The writer of a ...
(3,2) symmetric bilinear form defined by
:
 The projective space RP4 is the space of lines through the
The projective space RP4 is the space of lines through the origin
Origin(s) or The Origin may refer to:
Arts, entertainment, and media
Comics and manga
* Origin (comics), ''Origin'' (comics), a Wolverine comic book mini-series published by Marvel Comics in 2002
* The Origin (Buffy comic), ''The Origin'' (Bu ...
in R5 and is the space of nonzero vectors x in R5 up to scale, where x= (''x''0,''x''1,''x''2,''x''3,''x''4). The planar Lie quadric ''Q'' consists of the points ''xin projective space represented by vectors x with x · x = 0.
To relate this to planar geometry it is necessary to fix an oriented timelike line. The chosen coordinates suggest using the point ,0,0,0,0∈ RP4. Any point in the Lie quadric ''Q'' can then be represented by a vector x = λ(1,0,0,0,0) + v, where v is orthogonal
In mathematics, orthogonality is the generalization of the geometric notion of ''perpendicularity''.
By extension, orthogonality is also used to refer to the separation of specific features of a system. The term also has specialized meanings in ...
to (1,0,0,0,0). Since ''x∈ ''Q'', v · v = ''λ''2 ≥ 0.
The orthogonal space to (1,0,0,0,0), intersected with the Lie quadric, is the two dimensional celestial sphere
In astronomy and navigation, the celestial sphere is an abstract sphere that has an arbitrarily large radius and is concentric to Earth. All objects in the sky can be conceived as being projected upon the inner surface of the celestial sphere, ...
''S'' in Minkowski space-time
In mathematical physics, Minkowski space (or Minkowski spacetime) () is a combination of three-dimensional Euclidean space and time into a four-dimensional manifold where the spacetime interval between any two events is independent of the inerti ...
. This is the Euclidean plane with an ideal point at infinity, which we take to be ,0,0,0,1 the finite points (''x'',''y'') in the plane are then represented by the points ''v= ,''x'',''y'', −1, (''x''2+''y''2)/2 note that v · v = 0, v · (1,0,0,0,0) = 0 and v · (0,0,0,0,1) = −1.
Hence points x = ''λ''(1,0,0,0,0) + v on the Lie quadric with ''λ'' = 0 correspond to points in the Euclidean plane with an ideal point at infinity. On the other hand, points x with ''λ'' nonzero correspond to oriented circles (or oriented lines, which are circles through infinity) in the Euclidean plane. This is easier to see in terms of the celestial sphere
In astronomy and navigation, the celestial sphere is an abstract sphere that has an arbitrarily large radius and is concentric to Earth. All objects in the sky can be conceived as being projected upon the inner surface of the celestial sphere, ...
''S'': the circle corresponding to 'λ''(1,0,0,0,0) + v∈ ''Q'' (with ''λ'' ≠ 0) is the set of points y ∈ ''S'' with y · v = 0. The circle is oriented because v/''λ'' has a definite sign; minus;''λ''(1,0,0,0,0) + vrepresents the same circle with the opposite orientation. Thus the isometric
The term ''isometric'' comes from the Greek for "having equal measurement".
isometric may mean:
* Cubic crystal system, also called isometric crystal system
* Isometre, a rhythmic technique in music.
* "Isometric (Intro)", a song by Madeon from ...
reflection map x → x + 2 (x · (1,0,0,0,0)) (1,0,0,0,0) induces an involution ''ρ'' of the Lie quadric which reverses the orientation of circles and lines, and fixes the points of the
plane (including infinity).
To summarize: there is a one-to-one correspondence between points on the Lie quadric and ''cycles'' in the plane, where a cycle is either an oriented circle (or straight line) or a point in the plane (or the point at infinity); the points can be thought of as circles of radius zero, but they are not oriented.
Incidence of cycles
Suppose two cycles are represented by points ''x ''y∈ ''Q''. Then x · y = 0 if and only if the corresponding cycles "kiss", that is they meet each other with oriented first ordercontact
Contact may refer to:
Interaction Physical interaction
* Contact (geology), a common geological feature
* Contact lens or contact, a lens placed on the eye
* Contact sport, a sport in which players make contact with other players or objects
* ...
. If ''x∈ ''S'' ≅ R2 ∪ , then this just means that ''xlies on the circle corresponding to ''y this case is immediate from the definition of this circle (if ''ycorresponds to a point circle then x · y = 0 if and only if ''x= ''y.
It therefore remains to consider the case that neither ''xnor ''yare in ''S''. Without loss of generality, we can then take x= (1,0,0,0,0) + v and y = (1,0,0,0,0) + w, where v and w are spacelike unit vectors in (1,0,0,0,0)⊥. Thus
v⊥ ∩ (1,0,0,0,0)⊥ and w⊥ ∩ (1,0,0,0,0)⊥ are signature (2,1) subspaces of (1,0,0,0,0)⊥. They therefore either coincide or intersect in a 2-dimensional subspace. In the latter case, the 2-dimensional subspace can either have signature (2,0), (1,0), (1,1), in which case the corresponding two circles in ''S'' intersect in zero, one or two points respectively. Hence they have first order contact if and only if the 2-dimensional subspace is degenerate (signature (1,0)), which holds if and only if the span of v and w is degenerate. By Lagrange's identity
In algebra, Lagrange's identity, named after Joseph Louis Lagrange, is:
\begin
\left( \sum_^n a_k^2\right) \left(\sum_^n b_k^2\right) - \left(\sum_^n a_k b_k\right)^2 & = \sum_^ \sum_^n \left(a_i b_j - a_j b_i\right)^2 \\
& \left(= \frac \sum_^n ...
, this holds if and only if (v · w)2 = (v · v)(w · w) = 1, i.e., if and only if v · w = ± 1, i.e., x · y = 1 ± 1. The contact is oriented if and only if v · w = – 1, i.e., x · y = 0.
The problem of Apollonius
 The incidence of cycles in Lie sphere geometry provides a simple solution to the problem of Apollonius. This problem concerns a configuration of three distinct circles (which may be points or lines): the aim is to find every other circle (including points or lines) which is tangent to all three of the original circles. For a generic configuration of circles, there are at most eight such tangent circles.
The solution, using Lie sphere geometry, proceeds as follows. Choose an orientation for each of the three circles (there are eight ways to do this, but there are only four up to reversing the orientation of all three). This defines three points ''x ''y ''zon the Lie quadric ''Q''. By the incidence of cycles, a solution to the Apollonian problem compatible with the chosen orientations is given by a point ''q∈ ''Q'' such that q is orthogonal to x, y and z. If these three vectors are linearly dependent, then the corresponding points ''x ''y ''zlie on a line in projective space. Since a nontrivial quadratic equation has at most two solutions, this line actually lies in the Lie quadric, and any point ''qon this line defines a cycle incident with ''x ''yand ''z Thus there are infinitely many solutions in this case.
If instead x, y and z are linearly independent then the subspace ''V'' orthogonal to all three is 2-dimensional. It can have signature (2,0), (1,0), or (1,1), in which case there are zero, one or two solutions for ''qrespectively. (The signature cannot be (0,1) or (0,2) because it is orthogonal to a space containing more than one null line.) In the case that the subspace has signature (1,0), the unique solution q lies in the span of x, y and z.
The general solution to the Apollonian problem is obtained by reversing orientations of some of the circles, or equivalently, by considering the triples (x,''ρ''(y),z), (x,y,''ρ''(z)) and (x,''ρ''(y),''ρ''(z)).
Note that the triple (''ρ''(x),''ρ''(y),''ρ''(z)) yields the same solutions as (x,y,z), but with an overall reversal of orientation. Thus there are at most 8 solution circles to the Apollonian problem unless all three circles meet tangentially at a single point, when there are infinitely many solutions.
The incidence of cycles in Lie sphere geometry provides a simple solution to the problem of Apollonius. This problem concerns a configuration of three distinct circles (which may be points or lines): the aim is to find every other circle (including points or lines) which is tangent to all three of the original circles. For a generic configuration of circles, there are at most eight such tangent circles.
The solution, using Lie sphere geometry, proceeds as follows. Choose an orientation for each of the three circles (there are eight ways to do this, but there are only four up to reversing the orientation of all three). This defines three points ''x ''y ''zon the Lie quadric ''Q''. By the incidence of cycles, a solution to the Apollonian problem compatible with the chosen orientations is given by a point ''q∈ ''Q'' such that q is orthogonal to x, y and z. If these three vectors are linearly dependent, then the corresponding points ''x ''y ''zlie on a line in projective space. Since a nontrivial quadratic equation has at most two solutions, this line actually lies in the Lie quadric, and any point ''qon this line defines a cycle incident with ''x ''yand ''z Thus there are infinitely many solutions in this case.
If instead x, y and z are linearly independent then the subspace ''V'' orthogonal to all three is 2-dimensional. It can have signature (2,0), (1,0), or (1,1), in which case there are zero, one or two solutions for ''qrespectively. (The signature cannot be (0,1) or (0,2) because it is orthogonal to a space containing more than one null line.) In the case that the subspace has signature (1,0), the unique solution q lies in the span of x, y and z.
The general solution to the Apollonian problem is obtained by reversing orientations of some of the circles, or equivalently, by considering the triples (x,''ρ''(y),z), (x,y,''ρ''(z)) and (x,''ρ''(y),''ρ''(z)).
Note that the triple (''ρ''(x),''ρ''(y),''ρ''(z)) yields the same solutions as (x,y,z), but with an overall reversal of orientation. Thus there are at most 8 solution circles to the Apollonian problem unless all three circles meet tangentially at a single point, when there are infinitely many solutions.
Lie transformations
Any element of the group O(3,2) of orthogonal transformations of R3,2 maps any one-dimensional subspace of null vectors in R3,2 to another such subspace. Hence the group O(3,2)acts
The Acts of the Apostles ( grc-koi, Πράξεις Ἀποστόλων, ''Práxeis Apostólōn''; la, Actūs Apostolōrum) is the fifth book of the New Testament; it tells of the founding of the Christian Church and the spread of its message ...
on the Lie quadric. These transformations of cycles are called "Lie transformations". They preserve the incidence relation between cycles. The action is transitive and so all cycles are Lie equivalent. In particular, points are not preserved by general Lie transformations. The subgroup of Lie transformations preserving the point cycles is essentially the subgroup of orthogonal transformations which preserve the chosen timelike direction. This subgroup is isomorphic
In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word is ...
to the group O(3,1) of Möbius transformation
In geometry and complex analysis, a Möbius transformation of the complex plane is a rational function of the form
f(z) = \frac
of one complex variable ''z''; here the coefficients ''a'', ''b'', ''c'', ''d'' are complex numbers satisfying ''ad'' ...
s of the sphere. It can also be characterized as the centralizer of the involution ''ρ'', which is itself a Lie transformation.
Lie transformations can often be used to simplify a geometrical problem, by transforming circles into lines or points.
Contact elements and contact lifts
The fact that Lie transformations do not preserve points in general can also be a hindrance to understanding Lie sphere geometry. In particular, the notion of a curve is not Lie invariant. This difficulty can be mitigated by the observation that there is a Lie invariant notion of contact element. An oriented contact element in the plane is a pair consisting of a point and anoriented
In mathematics, orientability is a property of some topological spaces such as real vector spaces, Euclidean spaces, surfaces, and more generally manifolds that allows a consistent definition of "clockwise" and "counterclockwise". A space is ...
(i.e., directed) line through that point. The point and the line are incident cycles. The key observation is that the set of all cycles incident with both the point and the line is a Lie invariant object: in addition to the point and the line, it consists of all the circles which make oriented contact with the line at the given point. It is called a ''pencil
A pencil () is a writing or drawing implement with a solid pigment core in a protective casing that reduces the risk of core breakage, and keeps it from marking the user's hand.
Pencils create marks by physical abrasion, leaving a trail ...
of Lie cycles'', or simply a ''contact element''.
Note that the cycles are all incident with each other as well. In terms of the Lie quadric, this means that a pencil of cycles is a (projective) line lying entirely on the Lie quadric, i.e., it is the projectivization of a totally null two dimensional subspace of R 3,2: the representative vectors for the cycles in the pencil are all orthogonal to each other.
The set of all lines on the Lie quadric is a 3-dimensional manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a n ...
called the space of contact elements ''Z'' 3. The Lie transformations preserve the contact elements, and act transitively on ''Z'' 3. For a given choice of point cycles (the points orthogonal to a chosen timelike vector v), every contact element contains a unique point. This defines a map from ''Z'' 3 to the 2-sphere ''S'' 2 whose fibres are circles. This map is not Lie invariant, as points are not Lie invariant.
Let ''γ'': 'a'',''b''→ R2 be an oriented curve. Then ''γ'' determines a map ''λ'' from the interval 'a'',''b''to ''Z'' 3 by sending ''t'' to the contact element corresponding to the point ''γ''(''t'') and the oriented line tangent to the curve at that point (the line in the direction ''γ'' '(''t'')). This map ''λ'' is called the ''contact lift'' of ''γ''.
In fact ''Z'' 3 is a contact manifold
In mathematics, contact geometry is the study of a geometric structure on smooth manifolds given by a hyperplane distribution in the tangent bundle satisfying a condition called 'complete non-integrability'. Equivalently, such a distribution ...
, and the contact structure is Lie invariant. It follows that oriented curves can be studied in a Lie invariant way via their contact lifts, which may be characterized, generically as Legendrian curves in ''Z'' 3. More precisely, the tangent space to ''Z'' 3 at the point corresponding to a null 2-dimensional subspace ''π'' of R3,2 is the subspace of those linear map
In mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a Map (mathematics), mapping V \to W between two vect ...
s (A mod ''π''):''π'' → R3,2/''π'' with
: ''A''(x) · y + x · ''A''(y) = 0
and the contact distribution is the subspace Hom(''π'',''π''⊥/''π'') of this tangent space in the space Hom(''π'',R3,2/''π'') of linear maps.
It follows that an immersed Legendrian curve ''λ'' in ''Z'' 3 has a preferred Lie cycle associated to each point on the curve: the derivative of the immersion at ''t'' is a 1-dimensional subspace of Hom(''π'',''π''⊥/''π'') where ''π''=''λ''(''t''); the kernel of any nonzero element of this subspace is a well defined 1-dimensional subspace of ''π'', i.e., a point on the Lie quadric.
In more familiar terms, if ''λ'' is the contact lift of a curve ''γ'' in the plane, then the preferred cycle at each point is the osculating circle. In other words, after taking contact lifts, much of the basic theory of curves in the plane is Lie invariant.
Lie sphere geometry in space and higher dimensions
General theory
Lie sphere geometry in ''n''-dimensions is obtained by replacing R3,2 (corresponding to the Lie quadric in ''n'' = 2 dimensions) by R''n'' + 1, 2. This is Rn + 3 equipped with the symmetric bilinear form : :: The Lie quadric ''Q''''n'' is again defined as the set of ''x∈ RP''n''+2 = P(R''n''+1,2) with x · x = 0. The quadric parameterizes oriented (''n'' – 1)-spheres in ''n''-dimensional space, includinghyperplane
In geometry, a hyperplane is a subspace whose dimension is one less than that of its ''ambient space''. For example, if a space is 3-dimensional then its hyperplanes are the 2-dimensional planes, while if the space is 2-dimensional, its hyper ...
s and point spheres as limiting cases. Note that ''Q''''n'' is an (n + 1)-dimensional manifold (spheres are parameterized by their center and radius).
The incidence relation carries over without change: the spheres corresponding to points ''x ''y∈ ''Q''''n'' have oriented first order contact if and only if x · y = 0. The group of Lie transformations is now O(n + 1, 2) and the Lie transformations preserve incidence of Lie cycles.
The space of contact elements is a (2''n'' – 1)-dimensional contact manifold ''Z'' 2''n'' – 1: in terms of the given choice of point spheres, these contact elements correspond to pairs consisting of a point in ''n''-dimensional space (which may be the point at infinity) together with an oriented hyperplane
In geometry, a hyperplane is a subspace whose dimension is one less than that of its ''ambient space''. For example, if a space is 3-dimensional then its hyperplanes are the 2-dimensional planes, while if the space is 2-dimensional, its hyper ...
passing through that point. The space ''Z'' 2''n'' – 1 is therefore isomorphic to the projectivized cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold. It may be described also as the dual bundle to the tangent bundle. This may ...
of the ''n''-sphere. This identification is not invariant under Lie transformations: in Lie invariant terms, ''Z'' 2''n'' – 1 is the space of (projective) lines on the Lie quadric.
Any immersed oriented hypersurface in ''n''-dimensional space has a contact lift to ''Z'' 2''n'' – 1 determined by its oriented tangent spaces. There is no longer a preferred Lie cycle associated to each point: instead, there are ''n'' – 1 such cycles, corresponding to the curvature spheres in Euclidean geometry.
The problem of Apollonius has a natural generalization involving ''n'' + 1 hyperspheres in ''n'' dimensions.
Three dimensions and the line-sphere correspondence
In the case ''n''=3, the quadric ''Q''''3'' in P(R4,2) describes the (Lie) geometry of spheres in Euclidean 3-space. Lie noticed a remarkable similarity with the Klein correspondence for lines in 3-dimensional space (more precisely in RP3). Suppose ''x ''y∈ RP3, withhomogeneous coordinates
In mathematics, homogeneous coordinates or projective coordinates, introduced by August Ferdinand Möbius in his 1827 work , are a system of coordinates used in projective geometry, just as Cartesian coordinates are used in Euclidean geometry. T ...
(''x''0,''x''1,''x''2,''x''3) and (''y''0,''y''1,''y''2,''y''3).The following discussion is based on . Put ''p''''ij'' = ''x''''i''''y''''j'' - ''x''''j''''y''''i''. These are the homogeneous coordinates of the projective line joining ''x'' and ''y''. There are six independent coordinates and they satisfy a single relation, the Plücker relation
:''p''01 ''p''23 + ''p''02 ''p''31 + ''p''03 ''p''12 = 0.
It follows that there is a one-to-one correspondence between lines in RP3 and points on the Klein quadric
In mathematics, the lines of a 3-dimensional projective space, ''S'', can be viewed as points of a 5-dimensional projective space, ''T''. In that 5-space, the points that represent each line in ''S'' lie on a quadric, ''Q'' known as the Klein q ...
, which is the quadric hypersurface of points 'p''01, ''p''23, ''p''02, ''p''31, ''p''03, ''p''12in RP5 satisfying the Plücker relation.
The quadratic form
In mathematics, a quadratic form is a polynomial with terms all of degree two ("form" is another name for a homogeneous polynomial). For example,
:4x^2 + 2xy - 3y^2
is a quadratic form in the variables and . The coefficients usually belong to a ...
defining the Plücker relation comes from a symmetric bilinear form of signature (3,3). In other words, the space of lines in RP3 is the quadric in P(R3,3). Although this is not the same as the Lie quadric, a "correspondence" can be defined between lines and spheres using the complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form ...
s: if x = (''x''0,''x''1,''x''2,''x''3,''x''4,''x''5) is a point on the (complexified) Lie quadric (i.e., the ''x''''i'' are taken to be complex numbers), then
: ''p''01 = ''x''0 + ''x''1, ''p''23 = –''x''0 + ''x''1
: ''p''02 = ''x''2 + i''x''3, ''p''31 = ''x''2 – i''x''1
: ''p''03 = ''x''4 , ''p''12 = ''x''5
defines a point on the complexified Klein quadric (where i2 = –1).
Dupin cyclides
 Lie sphere geometry provides a natural description of Dupin cyclides. These are characterized as the common envelope of two one parameter families of spheres ''S''(''s'') and ''T''(''t''), where ''S'' and ''T'' are maps from intervals into the Lie quadric. In order for a common envelope to exist, ''S''(''s'') and ''T''(''t'') must be incident for all ''s'' and ''t'', i.e., their representative vectors must span a null 2-dimensional subspace of R4,2. Hence they define a map into the space of contact elements Z5. This map is Legendrian if and only if the derivatives of ''S'' (or ''T'') are orthogonal to ''T'' (or ''S''), i.e., if and only if there is an orthogonal decomposition of R4,2 into a direct sum of 3-dimensional subspaces ''σ'' and ''τ'' of signature (2,1), such that ''S'' takes values in ''σ'' and ''T'' takes values in ''τ''. Conversely such a decomposition uniquely determines a contact lift of a surface which envelops two one parameter families of spheres; the image of this contact lift is given by the null 2-dimensional subspaces which intersect ''σ'' and ''τ'' in a pair of null lines.
Such a decomposition is equivalently given, up to a sign choice, by a symmetric endomorphism of R4,2 whose square is the identity and whose ±1 eigenspaces are ''σ'' and ''τ''. Using the inner product on R4,2, this is determined by a quadratic form on R4,2.
To summarize, Dupin cyclides are determined by quadratic forms on R4,2 such that the associated symmetric endomorphism has square equal to the identity and eigenspaces of signature (2,1).
This provides one way to see that Dupin cyclides are cyclides, in the sense that they are zero-sets of quartics of a particular form. For this, note that as in the planar case, 3-dimensional Euclidean space embeds into the Lie quadric ''Q''3 as the set of point spheres apart from the ideal point at infinity. Explicitly, the point (x,y,z) in Euclidean space corresponds to the point
: , ''x'', ''y'', ''z'', –1, (''x''2 + ''y''2 + ''z''2)/2in ''Q''3. A cyclide consists of the points ,''x''1,''x''2,''x''3,''x''4,''x''5∈ ''Q''3 which satisfy an additional quadratic relation
:
for some symmetric 5 ×; 5 matrix ''A'' = (''a''''ij''). The class of cyclides is a natural family of surfaces in Lie sphere geometry, and the Dupin cyclides form a natural subfamily.
Lie sphere geometry provides a natural description of Dupin cyclides. These are characterized as the common envelope of two one parameter families of spheres ''S''(''s'') and ''T''(''t''), where ''S'' and ''T'' are maps from intervals into the Lie quadric. In order for a common envelope to exist, ''S''(''s'') and ''T''(''t'') must be incident for all ''s'' and ''t'', i.e., their representative vectors must span a null 2-dimensional subspace of R4,2. Hence they define a map into the space of contact elements Z5. This map is Legendrian if and only if the derivatives of ''S'' (or ''T'') are orthogonal to ''T'' (or ''S''), i.e., if and only if there is an orthogonal decomposition of R4,2 into a direct sum of 3-dimensional subspaces ''σ'' and ''τ'' of signature (2,1), such that ''S'' takes values in ''σ'' and ''T'' takes values in ''τ''. Conversely such a decomposition uniquely determines a contact lift of a surface which envelops two one parameter families of spheres; the image of this contact lift is given by the null 2-dimensional subspaces which intersect ''σ'' and ''τ'' in a pair of null lines.
Such a decomposition is equivalently given, up to a sign choice, by a symmetric endomorphism of R4,2 whose square is the identity and whose ±1 eigenspaces are ''σ'' and ''τ''. Using the inner product on R4,2, this is determined by a quadratic form on R4,2.
To summarize, Dupin cyclides are determined by quadratic forms on R4,2 such that the associated symmetric endomorphism has square equal to the identity and eigenspaces of signature (2,1).
This provides one way to see that Dupin cyclides are cyclides, in the sense that they are zero-sets of quartics of a particular form. For this, note that as in the planar case, 3-dimensional Euclidean space embeds into the Lie quadric ''Q''3 as the set of point spheres apart from the ideal point at infinity. Explicitly, the point (x,y,z) in Euclidean space corresponds to the point
: , ''x'', ''y'', ''z'', –1, (''x''2 + ''y''2 + ''z''2)/2in ''Q''3. A cyclide consists of the points ,''x''1,''x''2,''x''3,''x''4,''x''5∈ ''Q''3 which satisfy an additional quadratic relation
:
for some symmetric 5 ×; 5 matrix ''A'' = (''a''''ij''). The class of cyclides is a natural family of surfaces in Lie sphere geometry, and the Dupin cyclides form a natural subfamily.
See also
*Descartes' theorem
In geometry, Descartes' theorem states that for every four kissing, or mutually tangent, circles, the radii of the circles satisfy a certain quadratic equation. By solving this equation, one can construct a fourth circle tangent to three given, mu ...
, also can involve considering a line as a circle with infinite radius.
* Quasi-sphere
Notes
References
*Walter Benz
Walter Benz (May 2, 1931 Lahnstein – January 13, 2017 Ratzeburg) was a German mathematician, an expert in geometry.
Benz studied at the Johannes Gutenberg University of Mainz and received his doctoral degree in 1954, with Robert Furch as his ad ...
(2007) ''Classical Geometries in Modern Contexts: Geometry of Real Inner Product Spaces'', chapter 3: Sphere geometries of Möbius and Lie, pages 93–174, Birkhäuser, .
* .
* .
* .
* .
* Milson, R. (2000) "An overview of Lie’s line-sphere correspondence", pp 1–10 of ''The Geometric Study of Differential Equations'', J.A. Leslie & T.P. Robart editors, American Mathematical Society
The American Mathematical Society (AMS) is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, and serves the national and international community through its publications, meetings, ...
.
* {{citation, doi=10.1216/rmjm/1020171586, last1=Zlobec, first1= Borut Jurčič, last2= Mramor Kosta, first2= Neža, title=Configurations of cycles and the Apollonius problem, journal= Rocky Mountain Journal of Mathematics, volume= 31, pages= 725–744, year=2001, issn=0035-7596, url=http://math.la.asu.edu/~rmmc/rmj/Vol31-2/ZLO/ZLO.html, issue=2, doi-access=free.
External links
"On complexes - in particular, line and sphere complexes - with applications to the theory of partial differential equations"
English translation of Lie's key paper on the subject
"Oriented circles and 3D relativistic geometry"
An elementary video introducing concepts in Laguerre geometry (whose transformation group is a subgroup of the group of Lie transformations). The video is presented from the
rational trigonometry
''Divine Proportions: Rational Trigonometry to Universal Geometry'' is a 2005 book by the mathematician Norman J. Wildberger on a proposed alternative approach to Euclidean geometry and trigonometry, called rational trigonometry. The book advocat ...
perspective
Differential geometry
Incidence geometry
Conformal geometry