Lewis's Triviality Result on:
[Wikipedia]
[Google]
[Amazon]
In the mathematical theory of probability, David Lewis's triviality result is a theorem about the impossibility of systematically equating the conditional probability with the probability of a so-called conditional event, .
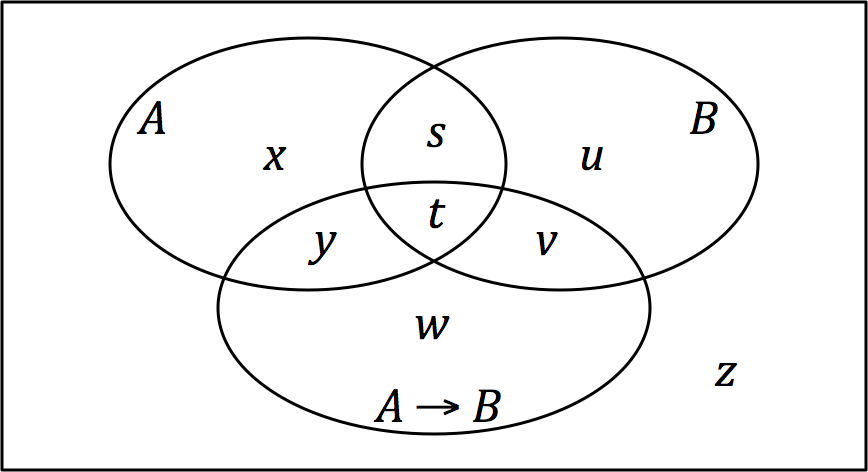 How might such a convention be combined with standard probability theory? The most direct extension of the standard theory would be to treat as an event like any other, i.e., as a set of outcomes. Adding to the familiar Venn- or
How might such a convention be combined with standard probability theory? The most direct extension of the standard theory would be to treat as an event like any other, i.e., as a set of outcomes. Adding to the familiar Venn- or
Conditional probability and conditional events
The statement "The probability that if , then , is 20%" means (put intuitively) that event may be expected to occur in 20% of the outcomes where event occurs. The standard formal expression of this is , where theconditional probability
In probability theory, conditional probability is a measure of the probability of an Event (probability theory), event occurring, given that another event (by assumption, presumption, assertion or evidence) is already known to have occurred. This ...
equals, by definition, .
Beginning in the 1960s, several philosophical logicians—most notably Ernest Adams and Robert Stalnaker
Robert Culp Stalnaker (born 1940) is an American philosopher who is Laurance S. Rockefeller Professor Emeritus of Philosophy at the Massachusetts Institute of Technology. He is a Fellow of the American Academy of Arts and Sciences and a Correspond ...
—floated the idea that one might also write , where is the conditional event "If , then ". That is, given events and , one might suppose there is an event, , such that could be counted on to equal , so long as .
Part of the appeal of this move would be the possibility of embedding conditional expressions within more complex constructions. One could write, say, , to express someone's high subjective degree of confidence ("75% sure") that either , or else if , then . Compound constructions containing conditional expressions might also be useful in the programming of automated decision-making systems.
 How might such a convention be combined with standard probability theory? The most direct extension of the standard theory would be to treat as an event like any other, i.e., as a set of outcomes. Adding to the familiar Venn- or
How might such a convention be combined with standard probability theory? The most direct extension of the standard theory would be to treat as an event like any other, i.e., as a set of outcomes. Adding to the familiar Venn- or Euler diagram
An Euler diagram (, ) is a diagrammatic means of representing Set (mathematics), sets and their relationships. They are particularly useful for explaining complex hierarchies and overlapping definitions. They are similar to another set diagrammi ...
of and would then result in something like Fig. 1, where are probabilities allocated to the eight respective regions, such that .
For to equal requires that , i.e., that the probability inside the region equal the region's proportional share of the probability inside the region. In general the equality will of course not be true, so that making it reliably true requires a new constraint on probability functions: in addition to satisfying Kolmogorov's probability axioms
The standard probability axioms are the foundations of probability theory introduced by Russian mathematician Andrey Kolmogorov in 1933. These axioms remain central and have direct contributions to mathematics, the physical sciences, and real-worl ...
, they must also satisfy a new constraint, namely that for any events and such that .
Lewis's result
pointed out a seemingly fatal problem with the above proposal: assuming a nontrivial set of events, the new, restricted class of -functions will not be closed underconditioning Conditioning may refer to:
Science, computing, and technology
* Air conditioning, the removal of heat from indoor air for thermal comfort
** Automobile air conditioning, air conditioning in a vehicle
** Ice storage air conditioning, air conditio ...
, the operation that turns probability function into new function , predicated on event 's occurrence. That is, if , it will not in general be true that as long as . This implies that if rationality requires having a well-behaved probability function, then a fully rational person (or computing system) would become irrational simply in virtue of learning that arbitrary event had occurred. Bas van Fraassen
Bastiaan Cornelis "Bas" van Fraassen (; ; born 5 April 1941) is a Dutch-American philosopher noted for his contributions to philosophy of science, epistemology and formal logic. He is a Distinguished Professor of Philosophy at San Francisco Stat ...
called this result "a veritable bombshell" (1976
Events January
* January 2 – The International Covenant on Economic, Social and Cultural Rights enters into force.
* January 5 – The Pol Pot regime proclaims a new constitution for Democratic Kampuchea.
* January 18 – Full diplomatic ...
, p. 273).
Lewis's proof is as follows. Let a set of events be non-trivial if it contains two possible events, and , that are mutually exclusive but do not together exhaust all possibilities, so that , , , and . The existence of two such events implies the existence of the event , as well, and, if conditional events are admitted, the event . The proof derives a contradiction from the assumption that such a minimally non-trivial set of events exists.
# Consider the probability of after conditioning, first on and then instead on its complement .
#* Conditioning on gives . But also, by the new constraint on -functions, . Therefore, .
#* Conditioning on gives . But also, . (The mutual exclusivity of and ensures that .) Therefore, .
# Instantiate the identity as . By the results from Step 1, the left side reduces to , while the right side, by the new constraint on -functions, equals . Therefore, , which means that , which contradicts the stipulation that . This completes the proof.
Graphical version
A graphical version of the proof starts with Fig. 2, where the and from Fig. 1 are now disjoint and has been replaced by .A proof starting with overlapping and , as in Fig. 1, would use mutually exclusive events and in place of and . By the assumption that and are possible, and . By the assumption that together and do not together exhaust all possibilities, . And by the new constraint on probability functions, , which means that :(1) Conditioning on an event involves zeroing out the probabilities outside the event's region and increasing the probabilities inside the region by a common scale factor. Here, conditioning on will zero out and and scale up and , to and , respectively, and so :(2) which simplifies to Conditioning instead on will zero out and and scale up and , and so :(3) which simplifies to From (2), it follows that , and since is the scaled-up value of , it must also be that . Similarly, from (3), . But then (1) reduces to , which implies that , which contradicts the stipulation that .Later developments
In a follow-up article, noted that the triviality proof can proceed by conditioning not on and but instead, by turns, on each of a finite set of mutually exclusive and jointly exhaustive events He also gave a variant of the proof that involved not total conditioning, in which the probability of either or is set to 1, but partial conditioning (i.e., Jeffrey conditioning), by which probability is incrementally shifted from to . Separately, pointed out that even without conditioning, if the number of outcomes is large but finite, then in general , being a ratio of two outputs of the -function, will take on more values than any single output of the function can. So, for instance, if in Fig. 1 are all multiples of 0.01 (as would be the case if there were exactly 100 equiprobable outcomes), then must be a multiple of 0.01, as well, but need not be. That being the case, cannot reliably be made to equal . also argued that the condition caused acceptable -functions to be implausibly sparse and isolated from one another. One way to put the point: standardly, any weighted average of two probability function is itself a probability function, so that between any two -functions there will be a continuum of weighted-average -functions along which one of the original -functions gradually transforms into the other. But these continua disappear if the added condition is imposed. Now an average of two acceptable -functions will in general not be an acceptable -function.Possible rejoinders
Assuming that holds for a minimally nontrivial set of events and for any -function leads to a contradiction. Thus can hold for any -function only for trivial sets of events—that is the triviality result. However, the proof relies on background assumptions that may be challenged. It may be proposed, for instance, that the referent event of an expression like “” is not fixed for a given and , but instead changes as the probability function changes. Or it may be proposed that conditioning on should follow a rule other than . But the most common response, among proponents of the condition, has been to explore ways to model conditional events as something other than subsets of a universe set of outcomes. Even before Lewis published his result, had modeled conditional events as ordered ''pairs'' of sets of outcomes. With that approach and others in the same spirit, conditional events and their associated combination and complementation operations do not constitute the usualalgebra of sets
In mathematics, the algebra of sets, not to be confused with the mathematical structure of ''an'' algebra of sets, defines the properties and laws of sets, the set-theoretic operations of union, intersection, and complementation and the re ...
of standard probability theory, but rather a more exotic type of structure, known as a conditional event algebra.
Notes
References
* * * * * * * {{refend Probability articles needing expert attention Logic Conditional probability