|
Lawler's Algorithm
Lawler's algorithm is an efficient algorithm for solving a variety of constrained scheduling problems, particularly single-machine scheduling. It can handle precedence constraints between jobs, requiring certain jobs to be completed before other jobs can be started. It can schedule jobs on a single processor in a way that minimizes the maximum tardiness, lateness, or any function of them. Definitions There are ''n'' jobs. Each job is denoted by i and has the following characteristics: * Processing-time, denoted by ''pi''; * Due time, denoted by ''d_i''. * Cost function, denoted by ''g_i''; it is a weakly-increasing function of the time job ''i'' completes its execution, denoted by ''F_i''. The objective function is min \, max_ \, g_i(F_i).Joseph Y-T. Leung. Handbook of scheduling: algorithms, models, and performance analysis. 2004. Some special cases are: * When g_i (F_i) = F_i - d_i = L_i, the objective function corresponds to minimizing the maximum lateness * When g_i (F_i) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Single-machine Scheduling
Single-machine scheduling or single-resource scheduling is an optimization problem in computer science and operations research. We are given ''n'' jobs ''J''1, ''J''2, ..., ''Jn'' of varying processing times, which need to be scheduled on a single machine, in a way that optimizes a certain objective, such as the throughput. Single-machine scheduling is a special case of identical-machines scheduling, which is itself a special case of optimal job scheduling. Many problems, which are NP-hard in general, can be solved in polynomial time in the single-machine case. In the standard three-field notation for optimal job scheduling problems, the single-machine variant is denoted by 1 in the first field. For example, " 1, , \sum C_j" is a single-machine scheduling problem with no constraints, where the goal is to minimize the sum of completion times. The makespan-minimization problem 1, , C_, which is a common objective with multiple machines, is trivial with a single machine, since the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Tardiness (scheduling)
In scheduling, tardiness is a measure of a delay in executing certain operations and earliness is a measure of finishing operations before due time. The operations may depend on each other and on the availability of equipment to perform them. Typical examples include job scheduling in manufacturing and data delivery scheduling in data processing networks. In manufacturing environment, inventory management considers both tardiness and earliness undesirable. Tardiness involves backlog issues such as customer compensation for delays and loss of goodwill. Earliness incurs expenses for storage of the manufactured items and ties up capital. Mathematical formulations In an environment with multiple jobs, let the deadline be d_i and the completion time be C_i of job i. Then for job i * lateness is L_i=C_i-d_i, * earliness is E_i = \max(0, d_i-C_i), * tardiness is T_i = \max(0, C_i-d_i). In scheduling common objective functions are C_\max, L_\max, E_\max, T_\max, \sum C_i, \sum L_i, \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
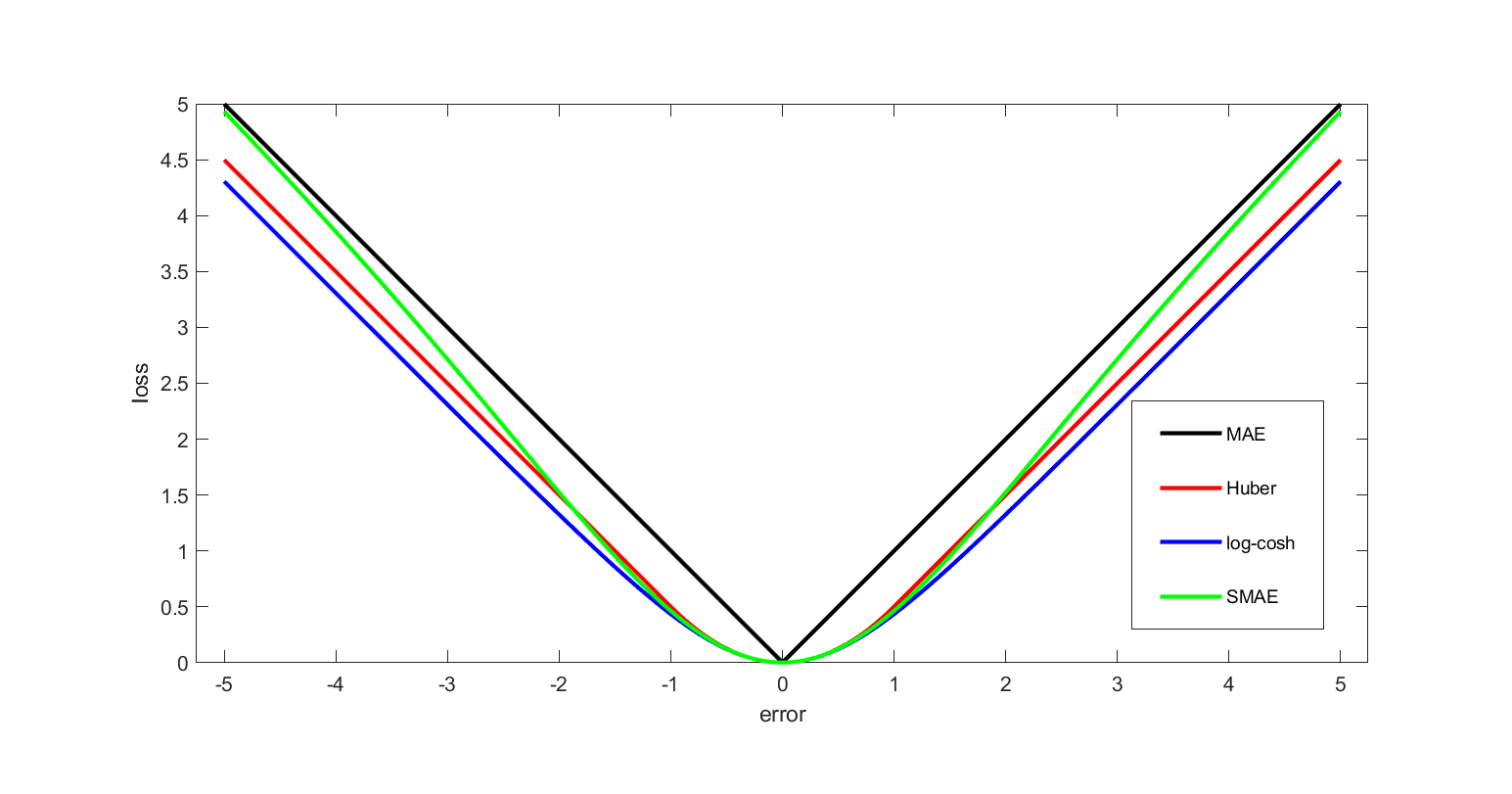
Objective Function
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite (in specific domains, variously called a reward function, a profit function, a utility function, a fitness function, etc.), in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy. In statistics, typically a loss function is used for parameter estimation, and the event in question is some function of the difference between estimated and true values for an instance of data. The concept, as old as Laplace, was reintroduced in statistics by Abraham Wald in the middle of the 20th century. In the context of economics, for example, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Lateness (scheduling)
In scheduling, tardiness is a measure of a delay in executing certain operations and earliness is a measure of finishing operations before due time. The operations may depend on each other and on the availability of equipment to perform them. Typical examples include job scheduling in manufacturing and data delivery scheduling in data processing networks. In manufacturing environment, inventory management considers both tardiness and earliness undesirable. Tardiness involves backlog issues such as customer compensation for delays and loss of goodwill. Earliness incurs expenses for storage of the manufactured items and ties up capital. Mathematical formulations In an environment with multiple jobs, let the deadline be d_i and the completion time be C_i of job i. Then for job i * lateness is L_i=C_i-d_i, * earliness is E_i = \max(0, d_i-C_i), * tardiness is T_i = \max(0, C_i-d_i). In scheduling common objective functions are C_\max, L_\max, E_\max, T_\max, \sum C_i, \sum L_i, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Production Planning
Production planning is the planning of Production (economics), production and manufacturing modules in a company or industry. It utilizes the resource allocation of activities of employees, raw material, materials and production capacity, in order to serve different customers.Fargher, Hugh E., and Richard A. Smith. "Method and system for production planning." U.S. Patent No. 5,586,021. 17 Dec. 1996. Different types of production methods, such as single item manufacturing, batch production, mass production, continuous production etc. have their own type of production planning. Production planning can be combined with production control into production planning and control, or it can be combined with enterprise resource planning. Overview Production planning is the future of production. It can help in efficient manufacturing or setting up of a production site by facilitating required needs. A production plan is made periodically for a specific time period, called the planning ho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |